
Пролог
Добрый день, уважаемые читатели. В данной статье я расскажу о том, как распарсить число, записанное прописью на русском языке.
Умным данный парсер делает возможность извлечения чисел из текста с ошибками, допущенными в результате некорректного ввода или в результате оптического распознавания текста из изображения (OCR).
Для ленивых:
Ссылка на проект github: ссылка.
От алгоритма до результата
В данном разделе будут описаны использованные алгоритмы. Осторожно, много букв!
Постановка задачи
По работе мне требуется распознать текст из печатного документа, сфотографированного камерой смартфона/планшета. Из-за соглашения о неразглашении информации я не могу привести пример фотографии, но суть в том, что в документе имеется таблица, в которой записаны некие показатели числом и прописью, и эти данные необходимо прочитать. Парсинг текста прописью необходим как дополнительный инструмент валидации, чтобы убедиться, что число распознано верно. Но, как известно, OCR не гарантирует точного распознавания текста. Например, число двадцать, записанное прописью, может быть распознано как «двадпать» или даже как «двапать». Нужно это учесть и извлечь максимальное количество информации, оценив величину возможной ошибки.
Примечание. Для распознавания текста я использую tesseract 4. Для .NET нет готового NuGet-пакета четвертой версии, поэтому я создал такой из ветки основного проекта, может кому пригодится: Genesis.Tesseract4.
Базовый алгоритм парсинга числа
Начнем с простого, а именно с алгоритма распознавания текста, записанного прописью, пока без ошибок. Если вам интересен именно умный парсинг, данный раздел можно пропустить.
Я не особо силен в гуглении, поэтому сходу не нашел готовый алгоритм для решения этой задачи. Впрочем, это даже к лучшему, т.к. алгоритм, придуманный самим, дает больше простора для кодинга. Да и сама задача оказалось интересной.
Итак, возьмем небольшое число, например «сто двадцать три». Оно состоит из трех слов (токенов), каждому из которых соответствует число, все эти числа суммируются:
"сто двадцать три" = сто + двадцать + три = 100 + 20 + 3 = 123Пока все просто, но копнем глубже, например рассмотрим число «двести двенадцать тысяч сто пять».
"двести двенадцать тысяч сто пять" = (двести + двенадцать) × тысяч + (сто + пять) = 212 * 1.000 + 105 = 212.105.Как видим, когда в числе присутствуют тысячи (а также миллионы и прочие степени тысячи), число делится на части, состоящие из локального маленького числа, в примере выше – 212, и множителя (1000). Таких фрагментов может быть несколько, но все они идут по убыванию множителя, например, за тысячей не может последовать миллион или еще одна тысяча. Это верно также и для частей маленького числа, так за сотнями не могут последовать сотни, а за десятками — десятки, поэтому запись «сто пятьсот» неверна. Характеристику, относящую два токена к одному типу, назовем уровнем, например, токены «сто» и «триста» имеют один уровень, и он больше, чем у токена «пятьдесят».
Из этих рассуждений и рождается идея алгоритма. Давайте выпишем все возможные токены (образцы), каждому из которых поставим в соответствие число, а также два параметра – уровень и признак множителя.
| Токен | Число | Уровень | Множитель? |
|---|---|---|---|
| ноль |
0 |
1 |
нет |
| один/одна |
1 |
1 |
нет |
| два/две |
2 |
1 |
нет |
| … |
… |
1 |
нет |
| девятнадцать |
19 |
1 |
нет |
| двадцать |
20 |
2 |
нет |
| … |
… |
2 |
нет |
| девяносто |
90 |
2 |
нет |
| сто |
100 |
3 |
нет |
| … |
… |
3 |
нет |
| девятьсот |
900 |
3 |
нет |
| тысяча/тысячи/тысяч |
1.000 |
4 |
да |
| миллион/миллиона/миллионов |
1.000.000 |
5 |
да |
| … |
… |
… |
да |
| квадриллион/квадриллиона/квадриллионов |
1.000.000.000.000.000 |
8 |
да |
На самом деле, в эту таблицу можно добавить и любые другие токены, в том числе для иностранных языков, только не забывайте, что в некоторых странах используется длинная, а не короткая система наименования чисел.
Теперь перейдем к парсингу. Заведем четыре величины:
- Глобальный уровень (globalLevel). Указывает, какой уровень был у последнего множителя. Изначально не определен и необходим для контроля. Если мы встретим токен-множитель, у которого уровень больше или равен глобальному, то это ошибка.
- Глобальное значение (globalValue). Общий сумматор, куда складывается результат результат перемножения локального числа и множителя.
- Локальный уровень (localLevel). Указывает, какой уровень был у последнего токена. Изначально не определен, работает аналогично глобальному уровню, но сбрасывается после обнаружения множителя.
- Локальное значение (localValue). Сумматор токенов, не являющихся множителями, т.е. чисел до 999.
Алгоритм выглядит следующим образом:
- Разбиваем строку на токены с помощью регулярки "\s+".
- Берем очередной токен, получаем информацию о нем из образца.
- Если это множитель:
- Если задан глобальный уровень, то убеждаемся, что он больше или равен уровню токена. Если нет – это ошибка, число некорректно.
- Устанавливаем глобальный уровень на уровень текущего токена.
- Умножаем величину токена на локальное значение и добавляем результат к глобальному значению.
- Очищаем локальное значение и уровень.
- Если это не множитель:
- Если задан локальный уровень, то убеждаемся, что он больше или равен уровню токена. Если нет – это ошибка, число некорректно.
- Устанавливаем локальный уровень на уровень текущего токена.
- Прибавляем к локальному значению величину токена.
- Возвращаем результат как сумму глобального и локального значений.
Пример работы для числа «два миллиона двести двенадцать тысяч сто восемьдесят пять».
| Токен |
globalLevel |
globalValue |
localLevel |
localValuе |
|---|---|---|---|---|
| – |
– |
– |
– |
|
| два |
– |
– |
1 |
2 |
| миллиона |
5 |
2.000.000 |
– |
– |
| двести |
5 |
2.000.000 |
3 |
200 |
| двенадцать |
5 |
2.000.000 |
1 |
212 |
| тысяч |
4 |
2.212.000 |
– |
– |
| сто |
4 |
2.212.000 |
3 |
100 |
| восемьдесят |
4 |
2.212.000 |
2 |
180 |
| пять |
4 |
2.212.000 |
1 |
185 |
Результатом будет 2.212.185.
Умный парсинг
Данный алгоритм можно использовать для реализации других сопоставлений, а не только для парсинга чисел, по этой причине я постараюсь описать его как можно подробнее.
С парсингом корректно записанного числа разобрались. Теперь давайте подумаем, какие ошибки могут быть при неверной записи числа, полученного в результате OCR. Другие варианты я не рассматриваю, но вы можете модифицировать алгоритм под конкретную задачу.
Я выделил три вида ошибок, с которыми столкнулся в процессе работы:
- Замена символов на другие со схожим начертанием. Например, буква «ц» почему-то заменяется на «п», а «н» на «и» и наоборот. При использовании третьей версии tesseract возможна замена буквы «о» на ноль. Эти ошибки, навскидку, самые распространенные, и требуют тюнинга под конкретную библиотеку распознавания. Так так принципы работы tesseract версий 3 и 4 имеют кардинальные различия, поэтому и ошибки там будут разными.
- Слияние токенов. Слова могут сливаться воедино (обратного пока не встречал). В комбинации с первой ошибкой порождает демонические фразы типа «двапатьодин». Попробуем раздраконить и таких монстров.
- Шум – левые символы и фразы в тексте. К сожалению, здесь мало что можно сделать на данный момент, но перспектива есть при сборе достаточно весомой статистики.
При этом сам алгоритм разбора, описанный выше, почти не меняется, главное различие в разбиении строки на токены.
Но начнем со сбора небольшой статистики использования букв в токенах. Из 33 букв русского языка при написании неотрицательных целых чисел используются только 20, назовем их хорошими буквами:
авдеиклмнопрстцчшыьяОстальные 13, соответственно, назовем плохими буквами. Максимальный размер токена при этом составляет 12 символов (13 при счете до квадриллионов). Подстроки длиной больше этой величины нужно разбивать.
Для сопоставления строк и токенов я решил использовать алгоритм Вагнера-Фишера, хотя и назвал его именем Левенштейна в коде. Редакционное предписание мне не нужно, поэтому я реализовал экономную по памяти версию алгоритма. Должен признаться, что реализация этого алгоритма оказалась более сложной задачей, чем сам парсер.
Небольшой ликбез: расстояние Левенштейна – частный случай алгоритма Вагнера-Фишера, когда стоимость вставки, удаления и замены символов статичны. В нашей задаче это не так. Очевидно, что если в подстроке мы встречаем плохую букву, то ее нужно заменить на хорошую, а вот заменять хорошую на плохую крайне нежелательно. Вообще говоря, нельзя, но ситуация зависит от конкретной задачи.
Для описания стоимости вставки, удаления и замены символов я создал такую таблицу: ссылка на таблицу с весами. Пока она заполнена методом трех П (пол, палец, потолок), но если заполнить ее данными на основе статистики OCR, то можно значительно улучшить качество распознавания чисел. В коде библиотеки присутствует файл ресурсов NumeralLevenshteinData.txt, в который можно вставить данные из подобной таблицы с помощью Ctrl+A, Ctrl+C и Ctrl+V.
Если в тексте встречается нетабличный символ, например, ноль, то стоимость его вставки приравнивается к максимальной величине из таблицы, а стоимость удаления и замены – к минимальной, таким образом алгоритм охотнее заменит ноль на букву «о», а если вы используете третью версию tesseract, то имеет смысл добавить ноль в таблицу и прописать минимальную цену для замены его на букву «о».
Итак, данные для алгоритма Вагнера-Фишера мы подготовили, давайте внесем изменения в алгоритм разбиения строки на токены. Для этого каждый токен мы подвергнем дополнительному анализу, но перед этим расширим информацию о токене следующими характеристиками:
- Уровень ошибки. Вещественное число от 0 (ошибки нет) до 1 (токен некорректен), означающее, насколько хорошо токен был сопоставлен с образцом.
- Признак использования токена. При разборе строки с вкраплениями мусора, часть токенов будет отброшена, для них данный признак выставляться не будет. При этом итоговая величина ошибки будет считаться как среднее арифметическое от ошибок использованных токенов.
Алгоритм анализа токенов:
- Пытаемся найти токен в таблице как есть. Если находим – все хорошо, возвращаем его.
- Если нет, то составляем список возможных вариантов:
Пытаемся сопоставить токен с образцом с помощью алгоритма Вагнера-Фишера. Данный вариант состоит из одного токена (сопоставленного образца) и его ошибка равна лучшему расстоянию, поделенному на длину образца.
Пример: токен «нуль» сопоставляется с образцом «ноль», при этом расстояние равно 0.5, т.к. стоимость замены плохой буквы «у» на хорошую «о» равна 0.5. Общая ошибка для данного токена будет 0.5 / 4 = 0.125.
Если подстрока достаточно большая (у меня это 6 символов), пытаемся поделить ее на две части минимум по 3 символа в каждой. Для строки в 6 символов будет единственный вариант деления: 3+3 символа. Для строки в 7 символов – уже два варианта, 3+4 и 4+3, и т.д. Для каждого из вариантов вызываем рекурсивно эту же функцию анализа токенов, заносим полученные варианты в список.
Чтобы не умирать в рекурсии, определяем максимальный уровень проваливания. Кроме того, варианты полученные в результате деления искусственно ухудшаем на некую величину (опция, по умолчанию 0.1), чтобы вариант прямого сопоставления был более ценным. Эту операцию пришлось добавить, т.к. подстроки типа «двапать» успешно делились на токены «два» и «пять», а не приводились к «двадцать». Увы, таковы особенности русского языка.
Пример: токен «двапать» имеет прямое сопоставление с образцом «двадцать», ошибка 0.25. Кроме того, лучшим вариантом деления является «два» + «пять» стоимостью 0.25 (замена «а» на «я»), ухудшенная искусственно до 0.35, в результате чего предпочтение отдается токену «двадцать».
- После составления всех вариантов выбираем лучший по минимальной сумме ошибок участвующих в нем токенов. Результат возвращаем.
Кроме того, в основной алгоритм генерации числа вводится проверка токенов, чтобы их ошибка не превышала некую величину (опция, по умолчанию 0.67). С помощью этого мы отсеиваем потенциальный мусор, хотя и не очень успешно.
Алгоритм в двух словах для тех, кому было лень читать текст выше
Входящую строку, представляющую число прописью мы разбиваем на подстроки с помощью регулярки \s+, затем каждую из подстрок пытаемся сопоставить с токенами-образцами или разбить на более мелкие подстроки, выбирая при этом лучшие результаты. В итоге получаем набор токенов, по которым генерируем число, а величину ошибки принимаем за среднее арифметическое ошибок среди токенов, использованных при генерации.
Заточка алгоритма под конкретную задачу
В моей задаче числа неотрицательные и относительно небольшие, поэтому я исключу ненужные токены от «миллиона» и выше. Для теста, уважаемые читатели, я, напротив, добавил дополнительные токены-жаргонизмы, что позволило парсить строки типа «пять кусков», «косарь двести» и даже «три стольника и два червонца». Забавно, но это даже не потребовало изменений в алгоритме.
Дальнейшее улучшение
У существующего алгоритма есть и недоработки:
- Контроль падежей. Строки «две тысячи» и «два тысячей» будут с нулевой ошибкой распознаны как 2000. В моей задаче контроль падежей не требуется, он даже вреден, но если вам нужна такая функция, это решается введением дополнительного флага в токен, отвечающего за падеж следующего токена.
- Отрицательные числа. Вводится дополнительный токен «минус» с особой обработкой. Ничего сложного, но не забудьте, что буква «у» является плохой, и не встречается в числительных, нужно будет изменить ее весовые характеристики или надеятся, что она не изменится в процессе OCR.
- Дробные числа. Решается заменой типа long на double и введением токенов «десятых», «сотых» и т.п… Не забудьте пересмотреть весы букв.
- Распознавание чисел, введенных пользователями. Т.к. при вводе текста вручную мы чаще всего допускаем ошибки, связанные с переТСановкой сиВМолов, следует добавить эту операцию в алгоритм Вагнера-Фишера.
- Поддержка других языков. Вводим новые токены, расширяем таблицу весов.
- Обработка мусора. В некоторых документах на данные налезает печать, качество изображением может быть плохим, ячейка может быть банально пустой. В этом случае в строку попадает мусор, который нужно как-то чистить. Лучшее, что я могу предложить на данный момент – производить предварительную обработку документа перед OCR. Мне очень сильно помогло удаление линий таблицы и заливка их цветом, близким к цвету свободного пространства ячейки. Это не решило все проблемы, но улучшило качество распознавания текста с документов, где таблица имела искривления из-за помятости документа или криворукого фотографа. В идеале стоит доворачивать саму ячейку и распознавать ее отдельно, если у вас, конечно, вообще имеется таблица.
Так что в итоге?
В проекте есть пример консольного приложения, бегущего по файлу samples.txt с примерами для парсера. Вот скриншот результатов:
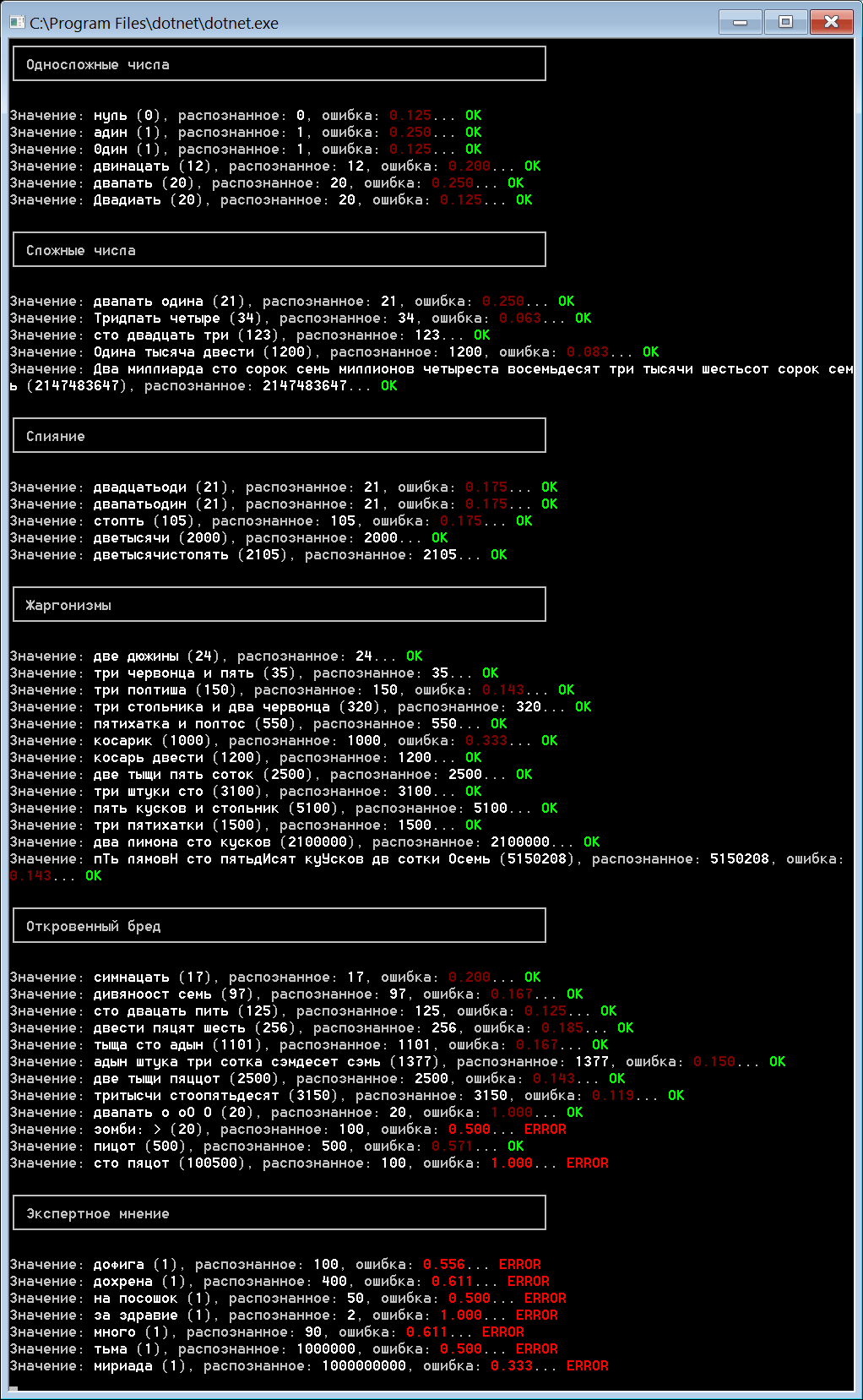
Оценивать результат поручаю вам, но как по мне, он неплох. Величина ошибки для реальных примеров распознавания не превышает 0.25, хотя я еще не прогонял весь набор имеющихся документов, наверное, не все там будет так гладко.
Что касается последнего раздела, мне всегда было интересно, сколько же это – «дофига». Также программа дала вполне себе адекватный ответ, сколько нужно принимать на посошок (я не употребляю, но все же) и даже точно определила значение древнерусского слова «тьма». И да, в вывод не вошла еще одна мера, которую воспитание добавить не позволило, но программа считает, что она равна тысяче =)
Пару слов о библиотеке
Изначально в мои планы не входило создание библиотеки, оформить ее я решил исключительно для хабра. Код постарался привести в порядок, но если будете использовать, делайте форк или копию, т.к. скорее всего вам не потребуются жаргонизмы и прочие токены, включенные в примеры.
Сама библиотека написана под .NET Standart 2.0 и C# 7.x, а алгоритмы легко переводятся на другие языки.
На случай возможного расширения библиотеки добавлю состав важных составляющих парсера чисел прописью (пространство имен Genesis.CV.NumberUtils):
- RussianNumber.cs – непосредственно парсер
- RussianNumber.Data.cs – файл с описанием токенов
- RussianNumber.ToString.cs – конвертер числа в текст прописью
- RussianNumberParserOptions.cs – опции парсера
- NumeralLevenshtein.cs – реализация алгоритма Вагнера-Фишера
- NumeralLevenshteinData.txt – ресурс, данные весов букв
Использование:
- RussianNumber.ToString(value) – преобразование числа в текст
- RussianNumber.Parse(value, [options]) – преобразование текста в число
Заключение
Очень надеюсь, что статья не показалась вам скучной даже несмотря на обилие текста. В последнее время у меня появилось множество тем, связанных с компьютерным зрением, о которых есть что рассказать, поэтому хотелось бы узнать мнение насчет такого формата статей. Что стоит добавить или, наоборот, удалить? Что больше интересно вам, читатели, сами алгоритмы или фрагменты кода?
Понравилась статья? Посмотрите другие: