Введение
Целью данной статьи является продемонстрировать способ вычисления алгебраического выражения, представленного в виде строки, посредством преобразования из инфиксной формы в постфиксную и парсинга (англ. parse - разбор) преобразованной строки.
Перед прочтением рекомендуется прочитать следующее:
Префиксная, инфиксная и постфиксная формы
Инфиксная форма - самая распространнёная форма, так как человека она проще для представления. Она представляет из себя выражение, в котором операторы располагаются между операндами. Отсюда исходит название данной формы.
Пример инфиксной формы:
Префиксная же форма представляет из себя выражение, в котором операторы находятся перед операндами:
Соответственно, постфиксная форма представляет из себя выражение, в котором оператор находится после операндов:
Для вычисления выражения, записанного в инфиксной формы, необходимо его предварительно проанализировать с учётом старшинства операторов и скобок. В свою очередь, префиксная и постфиксная формы такого не требуют, так как операторы записываются в порядке их вычисления и без скобок.
Выражения, записанные в префиксном или постфиксном виде, также называют бесскобочной или польской записью. Их называют польскими в честь автора - польского математика Ян Лукасевича.
Более подробно об представленных формах записи алгебраических выражений можно прочитать в Википедии.

Алгоритм Дейкстра
Для преобразования в постфиксную форму будем использовать улучшенный Эдсгером Вибе Дейкстрой алгоритм.
Принцип работы алгоритма Дейкстра:
Проходим исходную строку;
При нахождении числа, заносим его в выходную строку;
При нахождении оператора, заносим его в стек;
Выталкиваем в выходную строку из стека все операторы, имеющие приоритет выше рассматриваемого;
При нахождении открывающейся скобки, заносим её в стек;
При нахождении закрывающей скобки, выталкиваем из стека все операторы до открывающейся скобки, а открывающуюся скобку удаляем из стека.
Реализация алгоритма Дейкстры
Реализуем класс Mather, в котором определим приватные поля infixExpr для хранения инфиксного выражения, postfixExprдля постфиксного выражения и operationPriority, в котором определим список всех операторов и их приоритет:
public class Mather
{
// Хранит инфиксное выражение
public string infixExpr {get; private set; }
// Хранит постфиксное выражение
public string postfixExpr { get; private set; }
// Список и приоритет операторов
private Dictionary<char, int> operationPriority = new() {
{'(', 0},
{'+', 1},
{'-', 1},
{'*', 2},
{'/', 2},
{'^', 3},
{'~', 4} // Унарный минус
};
// Конструктор класса
public Mather(string expression)
{
// Инициализируем поля
infixExpr = expression;
postfixExpr = ToPostfix(infixExpr + "\r");
}
}В поле operationPriority скобка ('(') определена лишь для того, чтобы затем не выдавало ошибки при парсинге, а тильда ('~') добавлена для упрощения последующего разбора и представляет собой унарный минус.
Добавим приватный метод GetStringNumber, предназначенный для парсинга целочисленных значений:
/// <summary>
/// Парсинг целочисленных значений
/// </summary>
/// <param name="expr">Строка для парсинга</param>
/// <param name="pos">Позиция</param>
/// <returns>Число в виде строки</returns>
private string GetStringNumber(string expr, ref int pos)
{
// Хранит число
string strNumber = "";
// Перебираем строку
for (; pos < expr.Length; pos++)
{
// Разбираемый символ строки
char num = expr[pos];
// Проверяем, является символ числом
if (Char.IsDigit(num))
// Если да - прибавляем к строке
strNumber += num;
else
{
// Если нет, то перемещаем счётчик к предыдущему символу
pos--;
// И выходим из цикла
break;
}
}
// Возвращаем число
return strNumber;
}Далее создадим метод ToPostfix , который будет конвентировать в обратную польскую (постфиксную) запись:
private string ToPostfix(string infixExpr)
{
// Выходная строка, содержащая постфиксную запись
string postfixExpr = "";
// Инициализация стека, содержащий операторы в виде символов
Stack<char> stack = new();
// Перебираем строку
for (int i = 0; i < infixExpr.Length; i++)
{
// Текущий символ
char c = infixExpr[i];
// Если симовол - цифра
if (Char.IsDigit(c))
{
// Парсии его, передав строку и текущую позицию, и заносим в выходную строку
postfixExpr += GetStringNumber(infixExpr, ref i) + " ";
}
// Если открывающаяся скобка
else if (c == '(')
{
// Заносим её в стек
stack.Push(c);
}
// Если закрывающая скобка
else if (c == ')')
{
// Заносим в выходную строку из стека всё вплоть до открывающей скобки
while (stack.Count > 0 && stack.Peek() != '(')
postfixExpr += stack.Pop();
// Удаляем открывающуюся скобку из стека
stack.Pop();
}
// Проверяем, содержится ли символ в списке операторов
else if (operationPriority.ContainsKey(c))
{
// Если да, то сначала проверяем
char op = c;
// Является ли оператор унарным символом
if (op == '-' && (i == 0 || (i > 1 && operationPriority.ContainsKey( infixExpr[i-1] ))))
// Если да - преобразуем его в тильду
op = '~';
// Заносим в выходную строку все операторы из стека, имеющие более высокий приоритет
while (stack.Count > 0 && ( operationPriority[stack.Peek()] >= operationPriority[op]))
postfixExpr += stack.Pop();
// Заносим в стек оператор
stack.Push(op);
}
}
// Заносим все оставшиеся операторы из стека в выходную строку
foreach (char op in stack)
postfixExpr += op;
// Возвращаем выражение в постфиксной записи
return postfixExpr;
}Алгоритм вычисления постфиксной записи
После получения постфиксной записи, необходимо вычислить её значение. Для этого воспользуемся алгоримом очень похожим на прошлый алгоритмом, только этот будет использовать всего один стек.
Разберём принцип работы данного алгоритма:
Проходим постфиксную запись;
При нахождении числа, парсим его и заносим в стек;
При нахождении бинарного оператора, берём два последних значения из стека в обратном порядке;
При нахождении унарного оператора, в данном случае - унарного минуса, берём последнее значение из стека и вычитаем его из нуля, так как унарный минус является правосторонним оператором;
Последнее значение, после отработки алгоритма, является решением выражения.
Реализация алгоритма вычисления постфиксной записи
Создадим приватный метод Execute, который будет выполнять операции, соответствующие оператору и возвращать результат:
/// <summary>
/// Вычисляет значения, согласно оператору
/// </summary>
/// <param name="op">Оператор</param>
/// <param name="first">Первый операнд (перед оператором)</param>
/// <param name="second">Второй операнд (после оператора)</param>
private double Execute(char op, double first, double second) => op switch {
'+' => first + second, // Сложение
'-' => first - second, // Вычитание
'*' => first * second, // Умножение
'/' => first / second, // Деление
'^' => Math.Pow(first, second), // Степень
_ => 0 // Возвращает, если не был найден подходящий оператор
};Теперь реализуем сам алгоритм, создав метод Calc, в котором определим следующее:
public double Calc()
{
// Стек для хранения чисел
Stack<double> locals = new();
// Счётчик действий
int counter = 0;
// Проходим по строке
for (int i = 0; i < postfixExpr.Length; i++)
{
// Текущий символ
char c = postfixExpr[i];
// Если символ число
if (Char.IsDigit(c))
{
// Парсим
string number = GetStringNumber(postfixExpr, ref i);
// Заносим в стек, преобразовав из String в Double-тип
locals.Push(Convert.ToDouble(number));
}
// Если символ есть в списке операторов
else if (operationPriority.ContainsKey(c))
{
// Прибавляем значение счётчику
counter += 1;
// Проверяем, является ли данный оператор унарным
if (c == '~')
{
// Проверяем, пуст ли стек: если да - задаём нулевое значение,
// еси нет - выталкиваем из стека значение
double last = locals.Count > 0 ? locals.Pop() : 0;
// Получаем результат операции и заносим в стек
locals.Push(Execute('-', 0, last));
// Отчитываемся пользователю о проделанной работе
Console.WriteLine($"{counter}) {c}{last} = {locals.Peek()}");
// Указываем, что нужно перейти к следующей итерации цикла
// для того, чтобы пропустить остальной код
continue;
}
// Получаем значения из стека в обратном порядке
double second = locals.Count > 0 ? locals.Pop() : 0,
first = locals.Count > 0 ? locals.Pop() : 0;
// Получаем результат операции и заносим в стек
locals.Push(Execute(c, first, second));
// Отчитываемся пользователю о проделанной работе
Console.WriteLine($"{counter}) {first} {c} {second} = {locals.Peek()}");
}
}
// По завершению цикла возвращаем результат из стека
return locals.Pop();
}Испытание алгоритмов
Попробуем пропустить выражение 15/(7-(1+1))*3-(2+(1+1))*15/(7-(200+1))3-(2+(1+1))(15/(7-(1+1))*3-(2+(1+1))+15/(7-(1+1))*3-(2+(1+1))) через составленный алгоритм и посмотрим, верно ли он работает. Для ориентирования ниже представлен вариант решения от Яндекса.
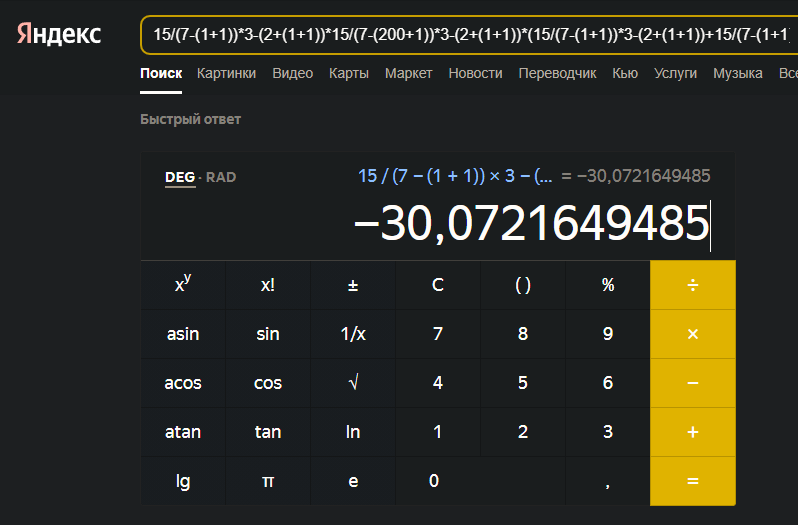
Код программы:
using MatherExecuter;
public class Program
{
static public void Main()
{
string expression = "15/(7-(1+1))*3-(2+(1+1))*15/(7-(200+1))*3-(2+(1+1))*(15/(7-(1+1))*3-(2+(1+1))+15/(7-(1+1))*3-(2+(1+1)))";
Mather mather = new(expression);
Console.WriteLine("Ввод: " + mather.infixExpr);
Console.WriteLine("Постфиксная форма: " + mather.postfixExpr);
Console.WriteLine("Итого: " + mather.Calc());
}
}Запустив данный код, мы получим следующее:

Итоги
Хоть реализованные здесь алгоритмы и работают, однако тут не учтены пробелы между символами, дробные значения, проверка на нуль в операции деления, не реализованы функции и тому подобное, поэтому данный код предствален лишь как пример.
Рекомендуется прочитать эту статью. В данной статье автор рассказывает, как реализовать полноценный интерпретатор математических выражений с поддержкой переменных, констант и функций. Однако в этой статье автор строит интерпретатор с использованием анализатора и парсера.