
В процессе изучения разных алгоритмов и структур данных приходит понимание, что не все они применимы в прикладных задачах (в отличие от задач про Васю и Петю/Алису и Боба). Но тот факт, что алгоритм/структура данных не является полезной на практике, не означает, что идеи в них содержащиеся не привлекают пытливые умы хотя бы из чистого любопытства. Потому речь пойдёт о красивых (субъективно) и, что важно, простых с точки зрения концепции структурах данных. И помните: если что-то не компилируется, это псевдокод.
Skiplist
Скиплист на уровне идеи очень интересный субъект мироздания: тут и объекты упорядочены, и вероятности прикрутили, и всё это делает его аналогом бинарного дерева поиска.
Построим его. Изначально имеем обычный односвязный отсортированный список. Пройдёмся по этому списку и выберем каждый элемент с некоторой вероятностью (обычно 0.5) во второй список. Крайние для удобства можно брать всегда. Проведём связи между соседями во втором списке и между выбранными копиями и оригинальными объектами. Получим что-то такое:
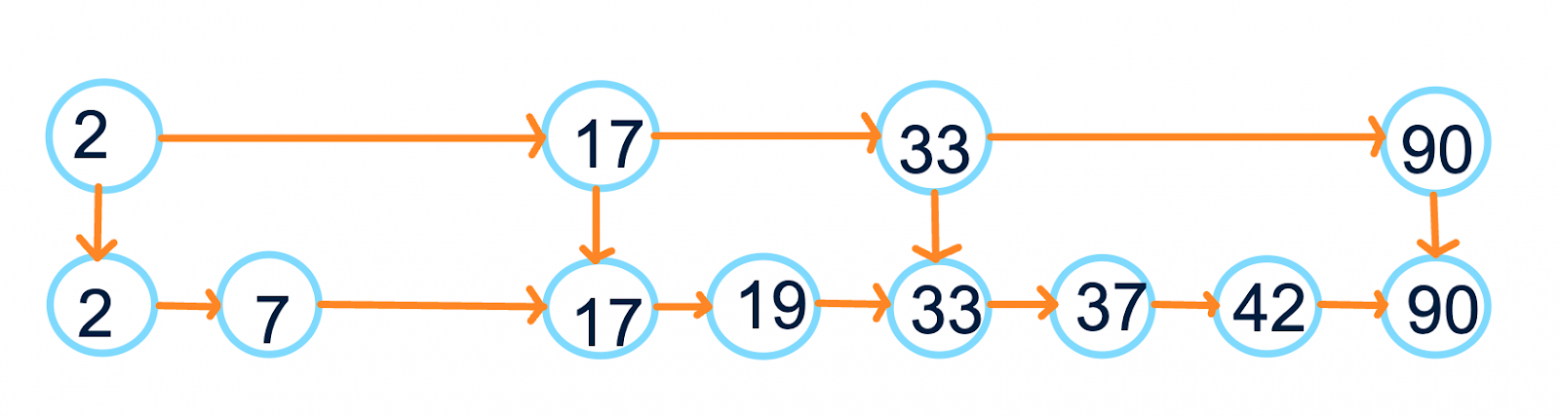
Повторим такую операцию, пока не решим, что достаточно. Ограничением можем считать конкретное ограничение на кол-во элементов в самом верхнем списке или просто закончить на ом уровне. Теперь у нас вот такая картина:
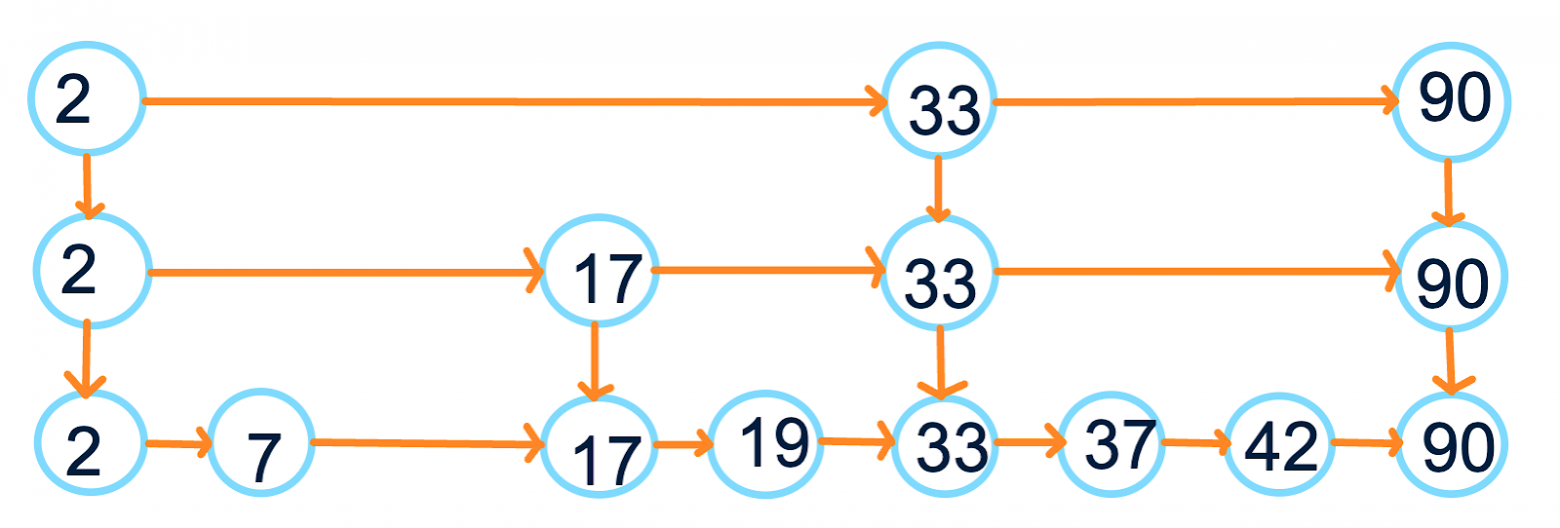
Что мы получили? Во-первых, умеем легко обходить все элементы скиплиста в отсортированном порядке. Во-вторых, умеем искать примерно за нужный элемент: начинаем с самого верхнего уровня и спускаемся по мере необходимости (смотрим на следующий элемент; если он больше искомого, двигаемся на уровень вниз):
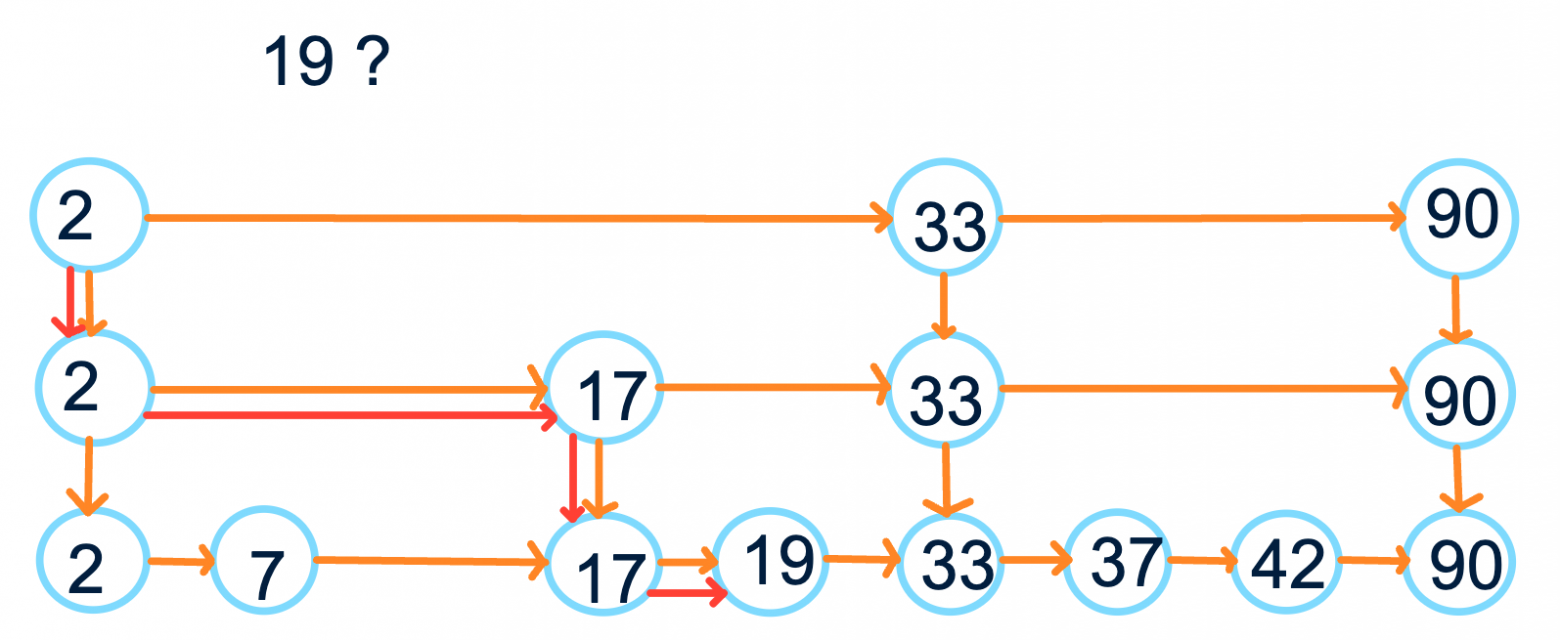
Раз уж мы взялись использовать списки, давайте использовать до конца: хочется быстро вставлять значение в такую структуру. Для вставки элемента найдём место, куда должен встать новый элемент, вставим его в изначальный список и с опять с какой-то вероятностью пропушим до некоторого уровня, пока рандом не решит, что пора остановиться. Аналогично можем удалять.
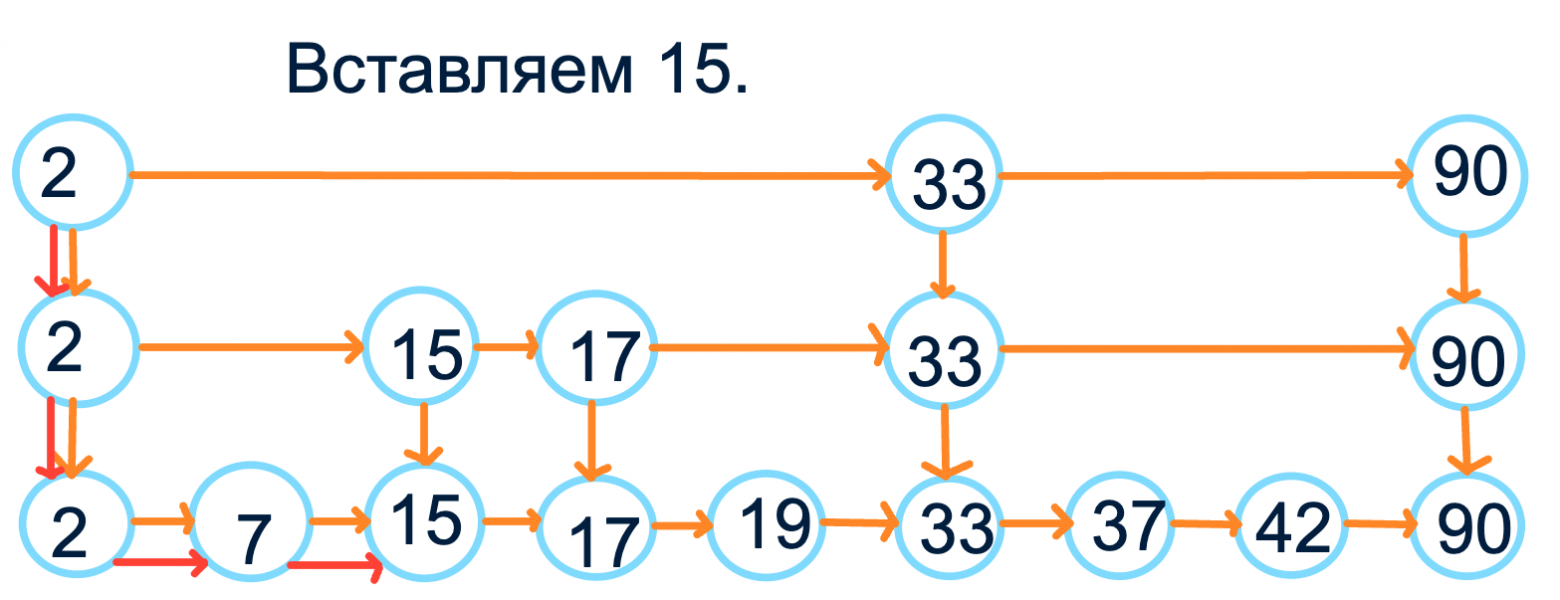
Теперь мы можем обходить все элементы за (и не как в bst с хранением предков и разбором случаев, а просто и понятно) + поиск элемента и его вставка/удаление за
в среднем. Только что памяти больше тратится, и эти вероятности нет-нет да и могут в какой-то вырожденный случай привести, но бог с ними.
Говорят, что скиплисты — очень хорошее решение, когда нужно что-то вроде thread-safe ordered set/map. Есть вот реализации для java и плюсов в folly.
Sideways heap
Sideways heap (кособокая куча?) – неявная куча, которая задаётся от самого левого листа:

Потом добавляется родитель и брат вершины (или сестра; no sexism):
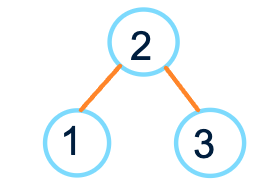
Развивая эту идею, получим что-то подобное:
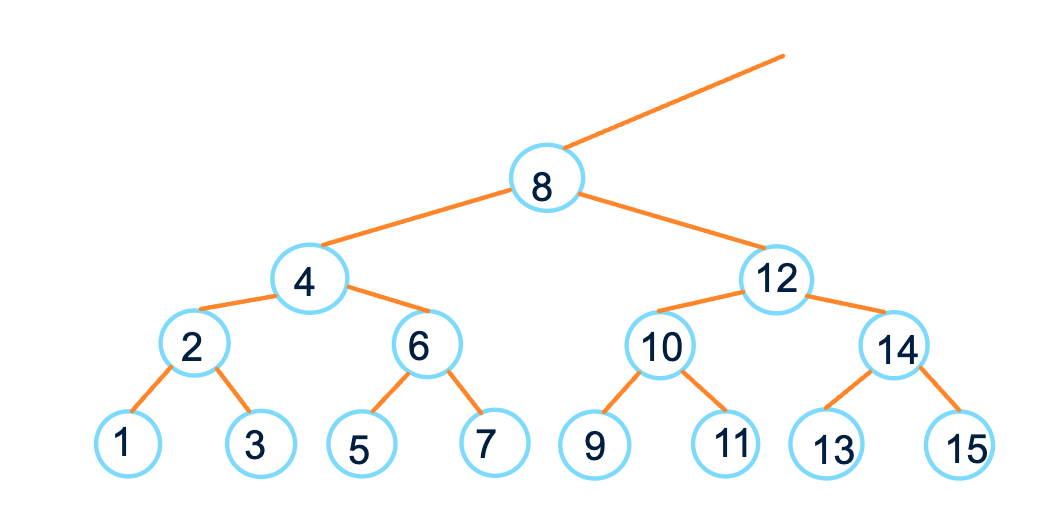
Если сделать проекцию кучи на числовую прямую, получим последовательность натуральных чисел.
Заметим, что все листья – это нечётные числа. Все числа на втором уровне – произведение двойки на нечётные числа. Все числа на третьем уровне – четвёрки на нечётные. И т.д. Ещё у этой кучи нет корня и бесконечно много листьев.
Попробуем по номеру вершины узнать всё её окружение. Пусть номер вершины k. Для начала научимся получать соседнюю вершину (для 1 (1 в бинарном виде) это 3 (11) и наоборот, для 2 (10) – 6 (110), для 4 (100) – 12 (1100), …, 2018 (11111100010) – 2022 (11111100110)). То есть нам нужно получить младший бит числа (k & -k), сдвинуть его влево и сделать xor c самим собой, i.e. получается как-то так:
int Sibling(int k) {
return k ^ ((k & -k) << 1);
}Для родителя и детей можно вывести следующие формулки:
int Parent(int k) {
int j = k & -k;
return (k - j) | (j << 1);
}
pair<int, int> Childrens(int k) {
int j = k & -k;
return ( k - (j >> 1), k + (j >> 1) ); // если j == 1, то получаем обратно k
}Конечно это очень специфическая структура данных, которая тем не менее позволяет делать какие-то интересные вещи. Например такие кучи используются как основа для других (имхо не сильно более полезных) структур данных. Но как по мне гораздо интереснее алгоритм нахождения наименьшего общего предка для вершин в дереве с на препроцессинг и честным
на запрос. Чуть подробнее о кучах и самом алгоритме можно посмотреть в лекции Кнута.
XOR-фильтр
XOR-фильтр предлагается как замена фильтрам Блума для случаев, когда множество ключей известно заранее, что позволяет быть более эффективным по времени и памяти.
XOR-фильтр есть множество ячеек по L бит (в отличие от фильтра Блума, в котором каждый отдельный бит независим). Например он может выглядеть так:

Теперь нам нужно выбрать три хеш-функции h1, h2 и h3 (на практике это одна и та же хеш-функция с тремя разными инициализирующими значениями), которые будут отображать наше значение x в ячейку массива. После того, как мы получаем по трём значениям h1(x), h2(x) и h3(x) L-битные значения (например нулевая, вторая и третья ячейки), посчитаем их xor:
Число 01110 называется кодом (table code) x. Тут ещё вводится четвёртая функция f, которая вычисляет f(x) – L-битный fingerprint числа x. Чтобы проверить, находится ли x в нашем множестве, мы сравниваем его код c его фингерпринтом. Если они равны, можем утверждать, что x почти наверняка в нашем множестве. Если не равны – точно не в нём.
Меняя значение L, мы можем повлиять на вероятность ошибки. Утверждается, что вероятность совпадения кода и фингерпринта примерно равна , потому если вы хотите допускать ошибку в
случаях, то можно брать
.
Самая интересная часть – это заполнить такую структуру. Процедура довольно крупная (в среднем занимает 100+ строк), потому опишем её в общих чертах.
Для хранения элементов создадим структуру объёмом
ячейки и будем следовать следующему алгоритму:
Если во множестве значений никого не осталось, мы закончили.
Выберем такой ключ
, что он хешируется в такую ячейку (ячейка
) в которую не хешируется никакой другой ключ.
Удаляем
из множества необработанных ключей и рекурсивно переходим к шагу 1.
Ячейке
нужно подобрать такое значение, чтобы f(x) совпадал с результатом xor всех значений для
(используем факт, что
).
Есть некоторая вероятность потерпеть неудачу на шаге 2, но авторы запруфали, что при указанном выше размере xor-фильтра она не очень большая. Если же у вас всё-таки не получилось найти подходящую ячейку, меняем seed у наших хеш-функций и начинаем заново. Хороший пример с картиночками есть вот тут.
Плюсы относительно фильтра Блума: если хочется повысить точность, нужно изменить количество битов в ячейке, а не количество хеш-функций; проверка наличия в фильтрах Блума обычно дольше (вычисляем много хеш-функций, потенциальный кеш-мисс на каждую из них, когда в xor-фильтре их всегда до трёх); занимаем меньше памяти (чаще всего).
Сообщество накодило репозиторий с реализациями для разных языков.
Sparse set
Sparse set это некоторый аналог std::vector<bool>/std::bitset за тем исключением, что в нём можно делать очистку всего множества за O(1). Вся структура – это два массива и одна переменная:
template <int R>
struct SparseSet {
int n = 0;
int dense[R];
int sparse[R];
};dense это массив значений. sparse же хранит индекс значения в dense, т.е. если dense[i] = v, то sparse[v] = i (вместо индекса можно хранить указатель). Тогда добавление выглядит так:
void Add(int val) {
dense[n] = val;
sparse[val] = n;
n++;
}и проверка на наличие:
bool Has(int val) {
return sparse[val] < n && dense[sparse[val]] == val;
}И тут мы умеем в “зануление” всей структуры: просто n = 0.
Выглядит довольно просто. Только что памяти она кушает гораздо больше, чем структуры, в которых можно использовать битовое сжатие. Приятным бонусом имеем, что при создании/обнулении структуры не нужно инициализировать используемые массивы: пусть там лежит мусор, который почистится при добавлении новых значений.
Также из него легко удалять элементы. Если элемент лежит в конце dense, достаточно просто уменьшить n. Иначе можно свапнуть нужный элемент с последним и опять же уменьшить размер.
Из самого популярного есть вот этот репозиторий. В folly есть реализация, но она почему-то insert-only (UPD: уже нет, мы это поправили). Тут можно почитать чуть подробнее.
Пополняемый массив
Пополняемый массив не столько структура, сколько классический метод обработки данных на простом примере.
Давайте будем решать следующую задачу (да, баян; да, не стыдно): в сортированном массиве требуется отвечать на запрос “сколько значений существует в массиве между l и r”. Примерно вот так:
class ReplArr {
vector<int> a;
ReplArr(vector<int> data) : a(data) {
sort(a);
}
int get(int l, r) {
return upper_bound(a, r) - lower_bound(a, l);
}
}А теперь давайте захотим добавлять элементы время от времени. Понятно, что вставка в середину массива работает не очень быстро. Включаем хак: будем хранить второй массив неупорядоченных элементов, в который будем докидывать приходящие значения и обрабатывать отдельно:
class ReplArr {
vector<int> a, b;
ReplArr(vector<int> data) : a(data) { sort(a); }
int get(int l, r) {
int rr = upper_bound(a, r);
int ll = lower_bound(a, l);
int res = rr - ll;
for (auto x: b) {
if (l <= i <= r) { res++; }
}
return res;
}
void add(int x) {
b.push_back(x);
}
}Работает! Только если у нас очень много добавлений, мы станем долго отвечать на запрос get. Давайте тогда время от времени докидывать все элементы b в a и сортировать заново. Время от времени это когда размер b примерно равен корню a (хотим, чтобы get и модифицированный add работали примерно одинаково, а раз их время работы это в интересующих нас случаях и
, можно взять
; формально асимптотики тут неверны, как минимум не хватает логарифма, но ради proof of concept мы им пренебрегли). Модифицированный
add:
void add(int x) {
b.push_back(x);
if (sqr(size(b)) >= size(a)) {
a += b;
sort(a);
b = vector<int>();
}
}В целом паттерн обрабатывать часть информации втупую и время от времени с ней разбираться довольно популярен (один из кейсов для кронтасок).
LSM
LSM - Log Structured Merge (key-value хранилище специфического вида). Здесь используется примерно та же идея, что и в предыдущей структуре. Суть в том, чтобы хранить данные на нескольких уровнях фиксированного размера (и, например, размеры растут в геометрической прогрессии). Как только первый уровень будет полностью заполнен, смержить его в следующий. Т.е. структуру следующего вида в целом можно назвать LSMом:
struct lsm {
vector<pair<K, V>> unsorted; // max 256
vector<pair<K, V>> sorted_c0; // ровно 256
vector<pair<K, V>> sorted_c1; // ровно 512
…
vector<pair<K, V>> sorted_ck; // ровно 65536
on_disk_storage* storage;
};Изначально вставляем в unsorted и производим по нему поиск втупую. Как только unsorted заполняется, скидываем все данные в sorted_c0 (очевидно, предварительно отсортировав). В следующий раз, при необходимости такой же операции, применяем условный mergesort и пихаем данные в sorted_c1. И т.д. При необходимости найти элемент, делаем линейный поиск по unsorted (небольшой размер и локальность данных помогут не очень сильно замедлиться) и бинпоиск по всем остальным векторам. Чтобы не делать поиск на больших медленных уровнях, можно рядом держать какой-нибудь фильтр Блума.
Чаще все структуры начиная с sorted_c0 являются каким-то хранилищем на диске, в то время как unsorted это какой-то in-memory контейнер (может даже скиплист). Также роль промежуточных структур вместо векторов может выполнять что угодно (например в LSM-tree, неожиданно, используются деревья).
Реализации можно найти у facebook и google.
Вместо заключения
Пока черновик статьи хранился на задворках гуглодоков, я обнаружил доклад Андрея Аксёнова про необычные структуры данных, которые ещё и используются на практике. Где-то мы пересеклись, где-то нет. В любом случае доклад посмотрите. Он хорош.
Реклама
Можно подписаться на мой канал про C++ и программирование в тг: t.me/thisnotes.