alizar 24 апр 2023 в 12:00

Математический подход к выбору девушки*. Правило 37%

Простой

7 мин

46K

Блог компании RUVDS.comМатематика*Научно-популярноеСоциальные сети и сообщества

В наше время многие находят вторую половинку в интернете: на тематических форумах и в онлайн-сообществах, в играх, на сайтах знакомств и приложениях вроде «Тиндера», где знакомства вообще поставлены на конвейер. Если десять лет назад 22% всех браков в США начинались со знакомства в интернете, то сейчас доля онлайн-знакомств превысила 39%. По сути, интернет стал основным способом знакомства мужчин и женщин, как долговременного, так и краткосрочного. Это очень удобно для гиков и специалистов с техническим образованием, поскольку мы получаем конкурентное преимущество, используя привычные инструменты. Например, можно поддерживать десятки чат-сессий в десктопном приложении или применять методы численного анализа в Excel/Google Sheets.

*Примечание. Под «девушкой» здесь и далее подразумевается любой объект, поочерёдно рассматриваемый из ограниченного пула схожих объектов с отличающимися характеристиками. Это может быть не только девушка, но и мужчина, квартира для съёма, автомобиль на вторичном рынке, домик в деревне, работодатель и т. д.

Если вы работали с ~~конвейером~~ приложениями для знакомств, то понимаете главную проблему: как выбрать оптимальный вариант из множества опций, которые рассматриваются по очереди? Проще говоря, когда остановиться?

Если вариант почти подходит по ряду параметров, то стоит остановится на нём или же отвергнуть — и продолжать поиск? Что будет оптимальной стратегией в условиях непредсказуемости и недостатка информации? К счастью, у этой проблемы есть чёткое математическое решение.

В 2017 году математик из Кембриджского университета Марианна Фрайбергер вывела правило 37%, которое назвала основным правилом стратегического дейтинга.

▍ Стратегический дейтинг

Проблему выбора можно сформулировать следующим образом:

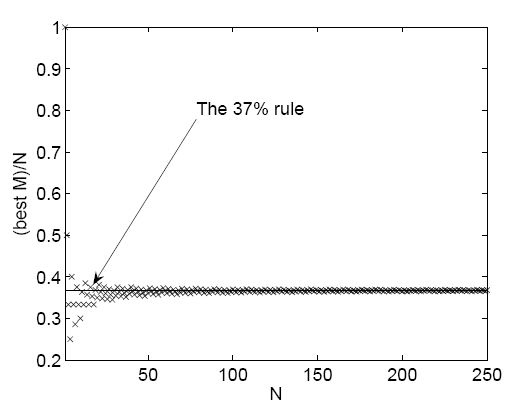
Какое количество возможных вариантов нужно перебрать, чтобы получить наилучший результат? С точки зрения математики, ответом будет 37%.

Оригинальное правило звучит так:

Из всех людей, с которыми вы можете встретиться, встречайтесь с первыми 37%, а затем выбирайте первого, кто лучше всех, кого вы видели раньше (или ждите самого последнего, если такой человек не найдётся).

Рис. 1

На практике вы не можете знать, с каким количеством женщин вы потенциально способны встретиться, поэтому придётся устанавливать рациональные ожидания.

Вот примерный алгоритм:

Предположим, вы хотите найти пару в течение года (долговременный партнёр, идеальная девушка для создания семьи).
Вы можете встречаться максимум с двумя девушками в неделю.
- Следовательно, общий пул для выбора составляет 104,3 девушки.
  - Примечание. Теоретически, общий пул можно рассчитать по адаптированной формуле Дрейка, которая создана для расчёта вероятности встречи с инопланетной цивилизацией:
    
    $N=R\cdot f_{p}\cdot n_{e}\cdot f_{l}\cdot f_{i}\cdot f_{c}\cdot L$
    
    То есть перемножить общее количество девушек в городе на долю девушек определённого возраста и образования, симпатичной внешности и готовых встречаться. Вы получите теоретически возможный максимальный пул.
Встречаемся с 38,6 девушек (104,3*0,37) в течение 135 дней (365*0,37). Очевидно, округляем девушек до 39.
После этого из оставшегося пула выбираем первую попавшуюся девушку, которая по общей оценке превосходит все 39 кандидаток, с кем вы встретились ранее.
- Exception. Если таковой не нашлось, то выбираем последнюю в списке или увеличиваем пул (продлеваем время просмотра) с перерасчётом формулы.

Алгоритм можно адаптировать для разных ситуаций, но базовый принцип остаётся тем же:

Просмотреть достаточное количество вариантов.
Затем выбрать первое же, что лучше всего, увиденного ранее.

Это правило не противоречит простой житейской мудрости: если выбрать слишком рано, то велик риск неоптимального выбора с последующим разочарованием. А если продолжать перебирать варианты до бесконечности, то все хорошие варианты разберут. То есть должен существовать некий оптимум.

▍ Вычисление оптимума

На рис. 1 общий пул кандидатов обозначен как $inline$ , а количество просмотренных кандидатов (назначенных свиданий) принято за $inline$ . Напоминаем, что по условиям алгоритма после $inline$ мы делаем окончательный выбор и останавливается на лучшем из всех, кого видели до сих пор. Крестиком $inline$ обозначен идеальный кандидат в пуле, которого мы ищем.

Наша задача — вычислить оптимальное соотношение $inline$ , которое необходимо для нахождения $inline$ .

Для этого вычисляется вероятность $inline$ встретить $inline$ после просмотра $inline$ кандидатов.

Очевидно, что если $inline$ встретился среди $inline$ , то мы упустили свой шанс и в остальной выборке никого лучше уже не найдём. Поэтому соотношение $inline$ не должно быть слишком большим и не может быть равно 1 (вероятность встретить там максимальный $inline$ равно $inline$ ). С другой стороны, оно не может быть и слишком маленьким, потому что тогда найденный объект будет ниже максимально возможного $inline$ по оценке, что приведёт к печальной ситуации в долговременной перспективе:

Последствия слишком малого $inline$

Если сложить вероятности встретить $inline$ для каждого последующего свидания, то получается:

$P(M,N)={1\over N}+{M\over {N(M+1)}}+{M\over {N(M+2)}}+...+{M\over {N(N-1)}}$

$={1\over N}\begin{pmatrix}1+{M\over {M+1}}+{M\over {M+2}}+...+{M\over {N-1}}\end{pmatrix}$

$={M\over N}\begin{pmatrix}{1\over M}+{1\over {M+1}}+{1\over {M+2}}+...+{1\over {N-1}}\end{pmatrix}$

Для каждого $inline$ мы хотим выбрать $inline$ с максимальной вероятностью $inline$ , то есть:

$display$

Если подставить сюда выражения из предыдущих уравнений, то получится:

$1<{1\over M}+{1\over {M+1}}+{1\over {M+2}}+...+{1\over {N-1}}$

Аналогично, для следующего человека $inline$ получается:

$1<{1\over {M+1}}+{1\over {M+2}}+{1\over {M+3}}...+{1\over {N-1}}$

В эти формулы можно подставлять настоящие цифры. Скажем, у нас выборка из четырёх девушек ( $inline$ ). В данном случае существует единственное значение $inline$ , которое удовлетворяет равенству, это $inline$ .

${5\over 6}={1\over 2}+{1\over 3}<1<{1\over 1}+{1\over 2}+{1\over 3}={11\over 6}$

То есть по алгоритму мы должны проигнорировать первую девушку (25% выборки), а из оставшихся выбрать первую же, которая будет лучше неё.

Если произвести такой расчёт для других размеров выборки, то можно выяснить, что с определённого размера выборки значение $inline$ приближается к $inline$ , а именно $inline$ . В частности, для выборки в сотни девушек это будет значение $inline$ , отсюда и «правило 37%». Всё просто.

Примечание. Задачу о разборчивой невесте (она же задача о секретаре или проблема остановки выбора), вероятно, впервые сформулировал математик Меррилл М. Флад в 1949 году. Первая публикация была сделана Мартином Гарднером в журнале Scientific American за февраль 1960 года (Who Solved the Secretary Problem?, Thomas S. Ferguson, Statist. Sci. 4(3): 282-289 (August, 1989). doi: 10.1214/ss/1177012493).

▍ Оптимизация отбора

Из расчётов выше можно понять, что для выбора оптимального объекта нам нужны критерии выбора, по которым мы можем их сравнивать и оценивать.

Понятно, что у каждого человека эти критерии свои, это может быть физическая привлекательность, ум, обаяние, чувство юмора, весёлый характер, добродушие, материальная состоятельность, уверенность в себе, счастье, здоровье, рост/вес и т. д. Какими бы критериями вы ни руководствовались, можно их формализовать и оценивать численно, чтобы сравнивать объекты друг с другом по общей оценке, но это не принципиально, потому что человек всё равно подсознательно выводит общую оценку, не вдаваясь в подкатегории. Достаточно простой оценки от 1 до 10, чтобы выбрать оптимальный результат по формуле выше.

Если нет желания пользоваться сайтами/приложениями для знакомств, то существует альтернатива — попросить девушек самих заполнять анкету, если они хотят с вами встречаться. Например, писатель и рационалист Якоб Фалькович (Jacob Falkovich) опубликовал такие анкеты для всех претенденток, которые хотят вступить с ним в платонические или романтические отношения:

Можно пойти ещё дальше. Другой интеллектуал и рационалист Деймон Саси (Damon Sasi) не просто разместил анкету на персональном сайте, но и открыл страничку с отзывами от бывших партнёрш (обе отзываются положительно, но отмечают отдельные недостатки субъекта).

Публикация на личном сайте (или в твиттере) анкеты для свиданий — отличная альтернатива сайтам знакомств. Такая анкета показывает, что вы открыты для отношений. По идее, среди посетителей вашего сайта только те девушки, которых привлекает ваша личность и/или работа, то есть первоначальный отбор проведён.

Даже если у вас нет личного сайта, можно создать документ Date Me в Google Docs или Dropbox Paper c описанием своей личности, фотографиями и списком того, что вы хотите от отношений. Вот пример такого документа от симпатичной программистки Кэтрин Олссон (Catherine Olsson) из компании AnthropicAI:

Ссылка публикуется в твиттере и соцсетях, в профиле на Хабре и т. д. Такая анкета с самопрезентацией сама по себе отсеивает неподходящих кандидатов. Остаются только те, кому вы действительно нравитесь. Сама Кэтрин называет эту стратегию «оптимизацией для партнёрских отношений».

А сайты знакомств тогда вообще не нужны.

Интернет стал основной площадкой для знакомств. Хотя многие по-прежнему относятся к нему негативно, но статистика показывает, что эта тенденция только усиливается. Если так пойдёт дальше, то знакомиться в офлайне станет совсем непривычно.

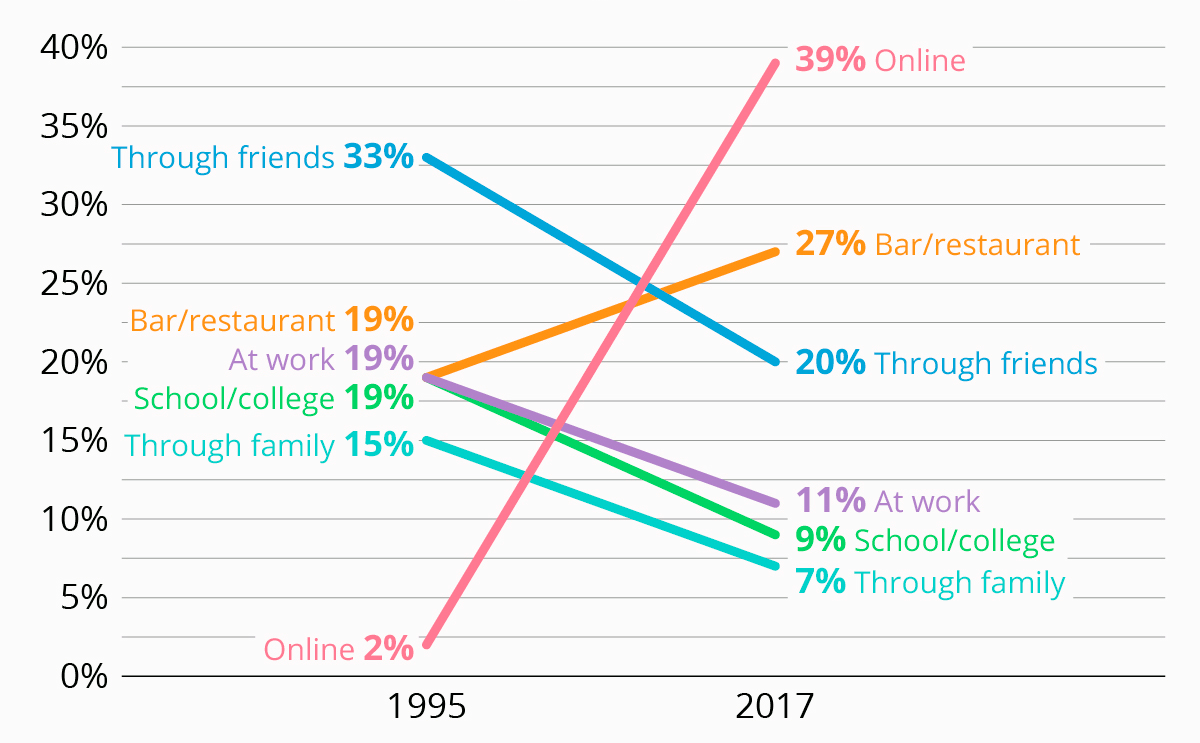
Доля гетеросексуальных пар США, которые познакомились одним из следующих способов (в таблицу не вошли другие варианты ответа: в церкви, по соседству). Опрос Стэнфордского университета, 5421 респондент

Даже сейчас люди в метро и на улице преимущественно сидят в телефонах и не слишком горят желанием смотреть по сторонам. Единственным исключением остаются бары/рестораны, куда народ приходит целенаправленно пообщаться. Так что методы знакомства постепенно эволюционируют. Способы пикапа, которые работали в нашей юности, сейчас выглядят немного кринжово.

В любом случае, «правило 37%» действует не только в отношении знакомств, но и для любых объектов, которые вы рассматриваете по очереди и хотите выбрать оптимальный.

Telegram-канал с розыгрышами призов, новостями IT и постами о ретроиграх 🕹️

Теги:

Хабы:

Математический подход к выбору девушки*. Правило 37%

▍ Стратегический дейтинг

▍ Вычисление оптимума

▍ Оптимизация отбора

Публикации

Информация