Привет! Меня зовут Дмитрий, и я хочу рассказать про нашу статью “Balancing Rational and Other-Regarding Preferences in Cooperative-Competitive Environments”, которую недавно приняли на конференцию AAMAS (A*).
В этой работе мы исследуем, как можно обучить группу агентов достигать собственные цели в смешанных средах, при этом не мешая или даже помогая друг другу. Мы разобрали несколько существующих решений и предложили свое. Пост получился высокоуровневый, технические детали есть в статье.

Кто мы
Меня зовут Дмитрий Иванов, я учусь на 3 курсе аспирантуры по экономике в Питерской Вышке. Работаю в группе “Агентные системы и обучение с подкреплением” в JetBrains Research, а также в Международной лаборатории теории игр и принятия решений в Вышке.
Эту работу мы сделали в соавторстве с Владимиром Егоровым, студентом 1 курса магистратуры “Программирование и анализ данных” в НИУ ВШЭ — Санкт-Петербург, и Алексеем Шпильманом, заведующим Центром анализа данных и машинного обучения в Вышке. Оба они также работают в JetBrains Research, Алексей -- руководитель нашей исследовательской группы.
Конфликт интересов
Глобально, проблема следующая: как обучить много агентов достигать собственные цели, при этом не мешая или даже помогая друг другу. Сложности появляются, когда между интересами агентов возникает конфликт. Одна из самых известных иллюстраций такого конфликта — дилемма заключенного (рис. 1).

В этой простой матричной игре два заключенных сидят на допросе. Они должны выбрать, что делать: молчать или давать показания против другого, при этом заключенные не могут коммуницировать друг с другом. Если оба заключенных предадут партнера, то их посадят на 3 года. Если оба заключенных кооперируются и молчат, то обоих посадят на 2 года. Наконец, если лишь один из заключенных предаст второго, то первого отпустят, а второго посадят на 4 года. Парадокс заключается в следующем: оба заключенных предпочтут взаимную кооперацию взаимному предательству, но при этом предательство является доминантным действием, т.е. обеспечивающим меньший срок независимо от действий другого агента. Про дилемму заключенного можно еще почитать у Юдковского.
Описанный парадокс — причина, по которой кооперации в мультиагентных средах добиться сложно (Peysakhovich and Lerer, 2017). Рациональные агенты выбирают доминантные действия, и всем плохо. Мы еще увидим примеры этого в экспериментах. Стоит упомянуть, что соответствие с дилеммой заключенного лишь концептуальное — в сложных мультиагентных средах обычно нет двух явных действий ‘Cooperate’ и ‘Defect’. Скорее, разные степени кооперативности поведения могут складываться из разных последовательностей низкоуровневых действий. Формализовать это соответствие пытались концептом Sequential Social Dilemma (Leibo et al., 2017), но, на мой взгляд, не особо удачно.
Кооперативные среды
Итак, в качестве мультиагентной системы, предлагаю держать в уме беспилотные автомобили — популярный в статьях пример (не потому ли, что примеров не так много?) Хотя у каждого автомобиля есть собственная цель, кооперация должна проявляться в соблюдении законов и правил безопасности. Как достигнуть и того, и другого? Конкретнее: как обучать агентов?
Один ответ: представить систему автомобилей централизованно как полностью кооперативную, как подразумевают в (Rashid et al., 2018). В этом случае все агенты оптимизируют одну и ту же общую награду: чтобы в среднем было меньше ДТП, быстрее достигался пункт назначения и т. п. Такую награду назовем общим или социальным благосостоянием (SW = Social Welfare):
Плюс максимизации SW в том, что в среднем, скорее всего, будет хорошо (эффективность). Минус — нет гарантий, что хорошо будет всем. То есть, не учитывается справедливость распределения наград. Что помешает такой системе “пожертвовать” несколькими неудачными агентами ради общего блага? Для примера обратимся еще раз к матрице дилеммы заключенного (Рис. 1). Системе, которая минимизирует суммарный срок, равнозначны результаты Defect-Cooperate и Cooperate-Cooperate: в обоих случаях суммарный срок равен 4 годам, несмотря на то, что один из вариантов гораздо справедливее! Упомяну, что можно подумать, как определить SW так, чтоб достигнуть и эффективности и справедливости — например, заменить сумму в формуле сверху на минимум. Мы исследуем этот вариант в статье, но этот пост и так неприлично долгий, поэтому не буду вдаваться в подробности
Несмотря на концептуальный недостаток, у полностью кооперативных систем есть техническое преимущество: для них придумали классные алгоритмы, такие как VDN, QMIX, COMA и пр. Эти алгоритмы нацелены на решение конкретной проблемы, которую можно назвать credit assignment или reward disentanglement — по сути, автоматическое определение вклада каждого агента в достижение общей цели. Представим себе систему из тысячи агентов — тех же автомобилей. Так как SW складывается из благосостояний отдельных агентов, наивное обучение конкретного агента на SW равносильно обучению на шуме — уж слишком слаб его вклад. Но вот эти алгоритмы способны такой вклад выделить — скорее всего, влияние агента будет сильное на себя и нескольких соседей, но незначительное на всех остальных.
Cooperative Reward Shaping
Другой ответ и аналог централизованной системе — обучать каждого агента на своей награде, в которой зашифрованы и личные, и социальные цели. В простом случае, который мы рассматриваем в статье, личные и социальные цели представляют собой индивидуальные и суммарные награды, перемешанные с предварительно заданным коэффициентом λ:

Обучение на такой награде (или ее социальной части) нередко встречается в статьях (Peysakhovich and Lerer, 2017; Lerer and Peysakhovich, 2019; Durugkar et al., 2020), но устоявшегося названия нет, поэтому мы обращаемся к такому обучению как Cooperative Reward Shaping (CRS). Плюсы и минусы такого подхода противоположны предыдущему. С одной стороны, каждый агент учитывает свою индивидуальность и не даст “принести себя в жертву”. С другой стороны, в этом случае нельзя применить классные алгоритмы, решающие credit assignment. То есть при достаточном числе агентов, социальная часть смешанной награды может быть очень шумной и бесполезной для обучения.
Наше решение
По сути, мы объединяем плюсы из двух перечисленных подходов: и учитываем индивидуальность агента, и применяем credit assignment алгоритмы из кооперативных сред. Идея такая: вместо обучения агента на награде, состоящей из двух компонент, мы обучаем на разных наградах две отдельные компоненты агента — эгоистичную и социальную. Обе компоненты играют роль при принятии решений, и важность каждой компоненты контролируется все тем же предварительно заданным коэффициентом. Довольно просто показать, что такие два подхода — смешивать награды при обучении или компоненты агента при выборе действий — математически эквивалентны. Но при нашем подходе социальную компоненту агента можно обучать с помощью тех классных алгоритмов — QMIX и COMA!
Все так просто? Ну, почти. Чтобы корректно складывать предсказания двух компонент, надо модифицировать их обучение. Кроме того, при подсчете SW мы комбинируем валью-функции, а не награды. Подробности расписывать не буду. Алгоритм, кстати, назвали BAROCCO — куда же без кликбейтового названия?
Эксперименты
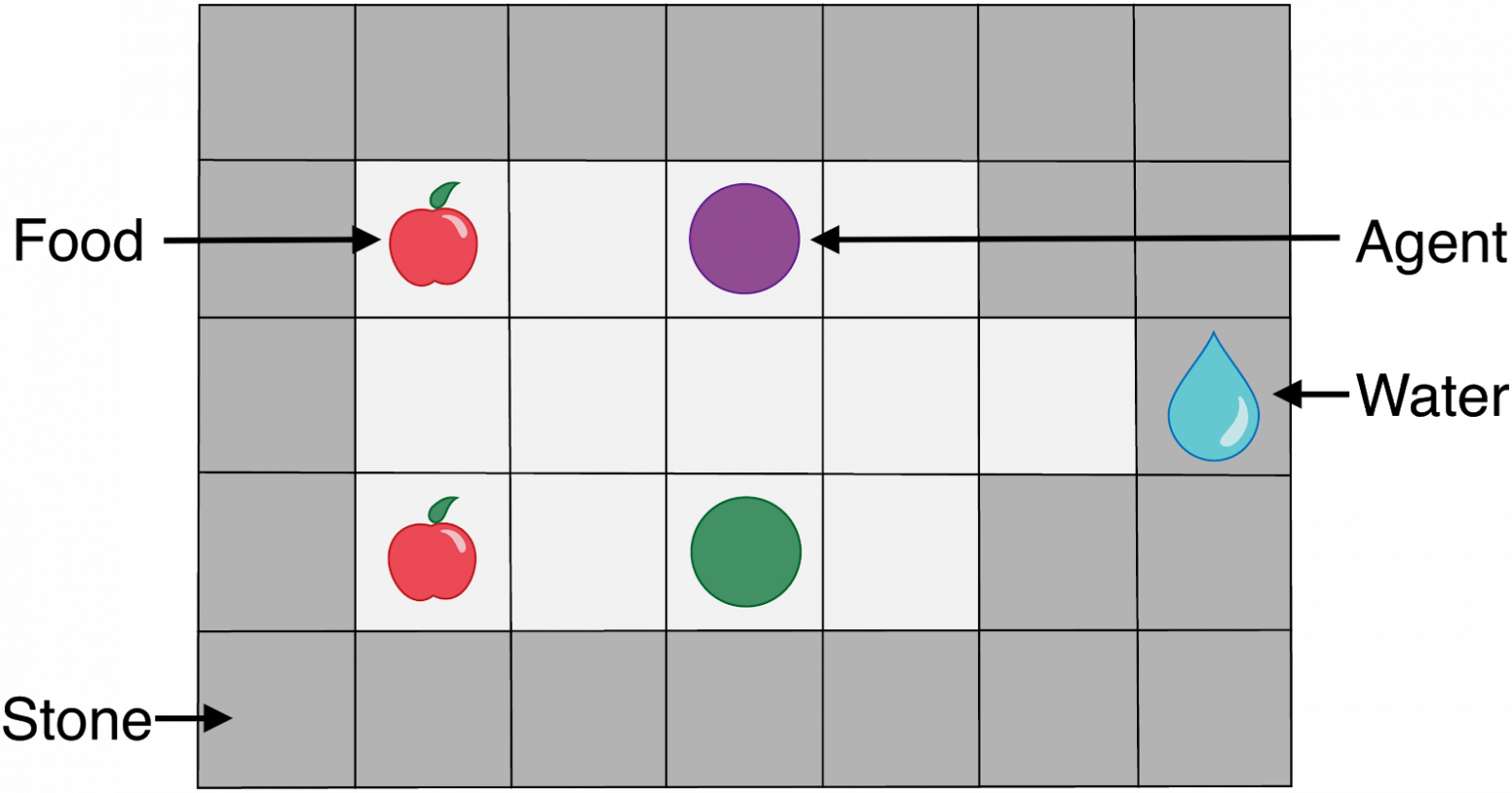
Эксперименты проводим в двух средах. Здесь приведу среду, которую мы предложили в нашей статье — Eldorado (Рис. 2). В ней два агента собирают воду и еду на маленькой карте. Цель каждого агента — прожить 1000 шагов, за что он получит награду +1. Если агент не достигает цели, то наоборот получает награду -1. Ресурсы необходимы агентам для выживания, и при их нехватке агенты теряют жизни. Еще агенты могут атаковать друг друга, что уменьшает жизни атакуемого и крадет у него ресурсы. При этом в среде достаточно ресурсов для обоих агентов, и для выполнения цели им достаточно скоординировать движение и удержаться от соблазна атаковать.
В экспериментах мы хотим:
Сравнить BAROCCO с бейзлайнами: selfish (эгоистичные агенты), CRS (социальные агенты), COMA (социальные агенты + credit assignment, но без наших модификаций обучения). В этих экспериментах эгоистичную компоненту мы выключаем при принятии решений везде, кроме соответствующего бейзлайна. В них мы проверяем, что наши модификации обучения работают.
Поварьировать социальность BAROCCO агентов, т.е. параметр λ. Ожидаем, что с увеличением параметра увеличивается средняя выживаемость, но может расти неравенство между агентами.

Рис. 3. Эксперименты в Eldorado. Сверху — сравнение с бейзлайнами. Для CRS и BAROCCO λ=1 , то есть эгоистичная компонента выключена. Для Selfish - наоборот, λ=0, то есть это BAROCCO или CRS с выключенной социальной компонентой. Снизу — варьируем λ для BAROCCO. Слева — средняя продолжительность жизни в сумме по обоим агентам, справа — индекс Джини, отражающий неравномерность выживаемости. По оси Х — время обучения в миллионах шагов в среде.
Результаты получили следующие:
По суммарной выживаемости BAROCCO показывает себя лучше остальных методов (левый верхний график), но достигает лишь около 1000 из возможных 2000 суммарной выживаемости. При этом, по высокому индексу Джини (правый верхний график) видно, что эта выживаемость делится неравномерно: один из агентов успешно достигает цели, в то время как второй стоит в стороне и не мешает. Учитывая, что ресурсов на карте хватает для обоих агентов, алгоритм в этом случае сошелся к локальному оптимуму. Тем не менее, концептуально этот результат иллюстрирует готовность полностью социального агента пожертвовать своей наградой.
Эгоистичные агенты показывают себя чуть хуже BAROCCO по суммарной выживаемости, но выживают примерно одинаковое количество шагов, что видно по низкому индексу Джини. Они хорошо координируют движения, но постоянно атакуют друг друга, и из-за этого не могут выживать дольше.
Социальные бейзлайны CRS и COMA совсем не справляются с обучением агентов. Проблема этих алгоритмов в применении к Eldorado в том, что они основаны на максимизации суммарной награды. Из-за того, что эта награда строго негативная (пока агенты не научатся выживать 1000 шагов), каждый агент вместо кооперации с союзником пытается не отхватить негативной награды от терминации союзника и, если сказать помягче, терминировать свой эпизод раньше. В результате, при обучении оба агента ищут способы не удлинить свои эпизоды, а наоборот.
Оказалось, что в этой среде уменьшение λ (коэффициента социальности) позволяет агентам сбежать из локального оптимума и обоим успешно выполнить цель. Лучше всего агенты проявили себя при коэффициенте равном 0.5. Такой результат показывает как ненулевая эгоистичная компонента может предотвращать готовность агентов жертвовать своей наградой.
Ограничения алгоритма

Одно из ограничений связано с необходимостью выбора коэффициента социальности λ. Он является гиперпараметром, который, во-первых, кроме как поиском по сетке значений не оптимизируется (что в мультиагентном обучении недешево), а во-вторых, непонятно как оптимизировать — минимально допустимые значения суммарной награды и максимально допустимые значения неравенства распределения наград могут быть свои для каждой среды. Как понимаем мы и как отмечали ревьюеры, было бы здорово автоматически подбирать или адаптировать этот гиперпараметр. Например, на основе принципа reciprocity (взаимности), подобно (Eccles et al., 2019; Lerer and Peysakhovich, 2019). В этом случае, агенты будут начинать взаимодействие с кооперативного поведения, но могут отклонится в случае отсутствия взаимности. Возможно, такой модификацией мы займемся в будущем.
Заключение
В представленной статье мы задались вопросом: какие могут быть желаемые свойства при обучении мультиагентных систем. Большинство существующих статей, изучающих смешанные среды, фокусируется только на общем благосостоянии. Мы хотим обратить внимание, что такой метрики недостаточно для смешанных сред, где каждый агент индивидуален, а не просто винтик в централизованном механизме, разделяющий глобальную цель с остальными агентами.