Feature Engineering или стероиды для ML моделей

Привет, чемпион!

Часто при построении ML моделей мало просто взять сильную модель. Оказывается, иногда грамотная предобработка данных существенно важнее. Сегодня речь пойдёт про feature engineering.

Рассмотрим несколько кейсов на эту тему более подробно. Данные будут упрощённые, но обещаю, от этого примеры не станут менее интересными ?.

Немного разомнёмся, рассмотрев простой двухмерный случай в задаче классификации. Здесь у нас будет два признака — их можно представить как координаты на плоскости, и целевой признак. Такую задачу легко визуализировать:

Тусклыми метками обозначены объекты из тестовой выборки, насыщенными — из обучающей. Цвет выбран в соответствии с меткой класса

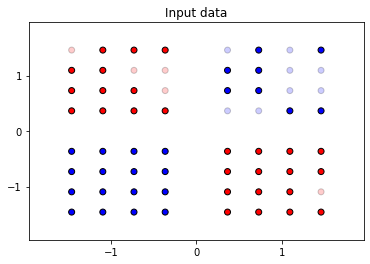
Закономерность видна невооружённым взглядом. Посмотрим, как с её поиском справятся разные алгоритмы машинного обучения.

Такая задача хороша тем, что мы можем наглядно визуализировать закономерности, по которым обученная ML модель разделяет объекты. Плюс — легко интерпретировать наблюдения. Давайте посмотрим, как разные алгоритмы машинного обучения решат нашу задачу, раскрасив области на плоскости в соответствие предсказаниям модели для них (чем больше интенсивность раскраски, тем больше «уверенность» модели в предсказании для этой области). Останавливаться на принципах их работы мы, пока что, не будем.

Лучше всего паттерн распознан решающим деревом. Обычно он работает хуже более сложного родственного ему случайного леса, но иногда более простой алгоритм может подходить лучше

Для начала рассмотрим последний вариант — алгоритм логистической регрессии. Не будем глубоко вдаваться в детали его работы, ознакомиться с ними можно, например, в учебнике ML ШАД. Что важно практически — так это то, что здесь будет иметь место линейная зависимость, что мы видим в отражении на графике выше. То есть такой алгоритм хорошо подходит тогда, когда классы хорошо разделимы прямой линией.

Ну а теперь первая задача

Вернёмся к данным. Утверждается, что в этой задаче можно разделить классы однозначенно!
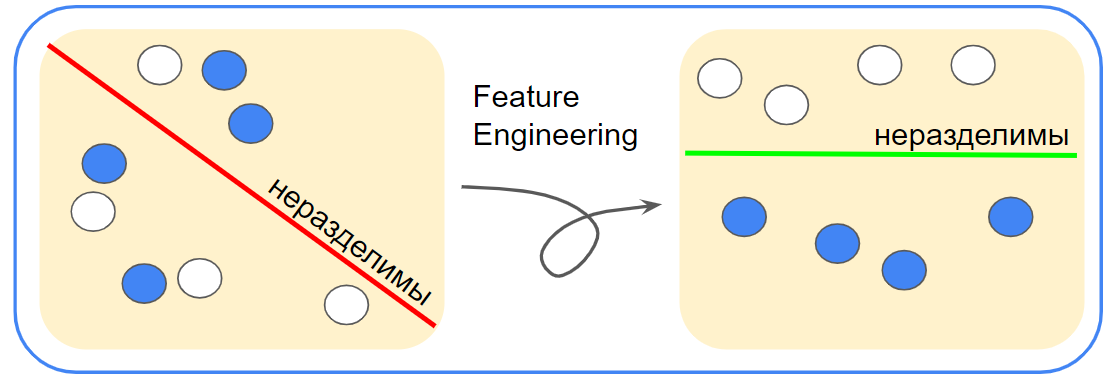
Но как? Существует такое преобразование признаков, при котором объекты можно будет разделить прямой линией с помощью алгоритма логистической регрессии со 100% точностью. Давайте ещё раз посмотрим на данные. Как можно преобразовать признаки, чтобы точки можно было разделить одной прямой?

Заменим одну из координат каждой точки на их произведение

Нужно перенести все точки одного цвета в одну сторону. Заменим одну из координат каждой точки на произведение её координат, тогда мы получим такую картину:

Как видно — модель идеально разделила классы между собой, хотя до этого это было невозможно.

Ну и, строго говоря, мы можем вообще оба старых признака для каждого объекта исключить и заменить на новый: произведение известных изначально признаков. Тогда объекты можно разделить в линейном пространстве, на прямой, относительно нуля. Это видно и на графике. Граница практически не смещается при перемещении в вертикальном направлении.

Вторая задача

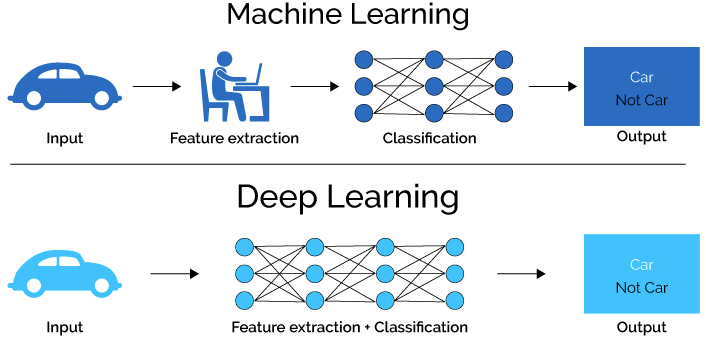
Вторая задача будет уже немного сложнее. Ранее рассмотренный приём можно отнести к элементарному «feature engineering». Конструирование признаков, feature engineering, в классическом машинном обучении зачастую является ключом к существенному увеличению качества. В отличие от глубинного обучения, где в большей степени решает архитектура сети. Недаром часто говорят о важности наглядного представления взаимосвязей между признаками в данных. Исследуя эти взаимосвязи, мы можем конструировать новые полезные признаки, исключать вредные, правильно подбирать алгоритмы для решения задачи и т.д.

Отличие классического ML и DL

Теперь приступим к самой задаче. У нас есть некоторые данные, где представлены объекты двух классов с метками «A» и «B», по условию задачи нам нужно получить модель на основе алгоритма логистической регрессии, которая позволит получить 100% долю правильных ответов.

Код

path = 'https://raw.githubusercontent.com/a-milenkin/Datasetes_for_Piplines/main/interview/simple_classification.csv',
df = pd.read_csv(path, index_col=0) # Загрузим данные
df.head()

	features_1	features_2	features_3	label
0	2.5	0.00	58	B
1	2.5	0.02	61	B
2	2.5	0.05	33	B
3	2.5	0.07	89	B
4	2.5	0.10	58	B

Давайте попробуем решить задачу, что называется, «в лоб».

Базовый набор умений Data Scientist'а (нет)

Проведём минимальную подготовку данных, выделим обучающие признаки и целевую переменную, подготовим выборку для контроля качества данных:

Код

X = df.drop('label', axis=1) #извлечём фичи
y = df['label'] # извлечём таргет
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=42
) #отложим тестовую выборку

Инициализируем и обучим модель, оценим accuracy полученной модели на отложенной тестовой выборке:

Код

model = LogisticRegression(n_jobs=-1, penalty='none') #инициализируем модель
model.fit(X_train, y_train) #обучаем модель на обучающих данных
model.score(X_test, y_test) #получим значение accuracy на тесте

Полученная в лоб точность: 0.489

Как можно заметить, примерно только половина ответов модели являются правильными. Давайте теперь подойдём к решению задачи немного более интеллектуально. Во-первых, в задачах классификации важную роль играет баланс классов (если один из классов будет представлен значительно меньшим числом объектов, то это может негативно сказаться на предиктивных способностях модели), а модель логистической регрессии можно настраивать, подбирая оптимальные гиперпараметры. Делать этого по условию нам ведь не запрещали.

Код

'''
Вернём долю в данных каждого из уникальных значений целевого признака
с помощью метода pandas.Series.value_counts
'''
y.value_counts(normalize=True) #normalize отвечает за нормирование значений кол-ва

B 50%, A 50%

ОК, данные сбалансированные, работа с балансом классов не должна принести пользы для нашей задачи. Подберём же оптимальные гиперпараметры алгоритма по очень широкой сетке гиперпараметров, настроив его под нашу задачу.

Код подбора гиперпараметров

param_grid = { #инициализация сетки параметров
'penalty': ['l1', 'l2', 'elasticnet', 'none'],
'dual': [False, True],
'C': np.logspace(-2, 3, 5),
'fit_intercept': [True, False],
'intercept_scaling': np.linspace(0, 1, 5),
'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'],
'max_iter': np.linspace(100, len(y_train), 5),
'l1_ratio':  np.linspace(0, 1, 5)
}
'''
GridSearchCV — один из инструментов для настройки моделей, встроенный в sklearn
'''
clf = GridSearchCV(model, param_grid, n_jobs=-1, verbose=3)
clf.fit(X_train, y_train)
clf.best_score_

Доля правильных ответов путём подборов параметров достигла уже примерно 0,52. Лучше, но всё ещё недостаточно хорошо. Как быть?

▍ EDA или исследуем признаки визуально

Код визуализации

sns.pairplot( # матрица диаграмм рассеяния из Seaborn
data = df, # данные
hue = 'label', # имя столбца в данных для раскраски меток
corner = True # матрица симметрична, не будем выводить лишние графики
).fig.suptitle( # настройки заголовка
'Зависимости для признаков', # заголовок
y = 1.08 # расположение
);

Наглядное представление позволяет увидеть закономерности практически любой природы при их наличии

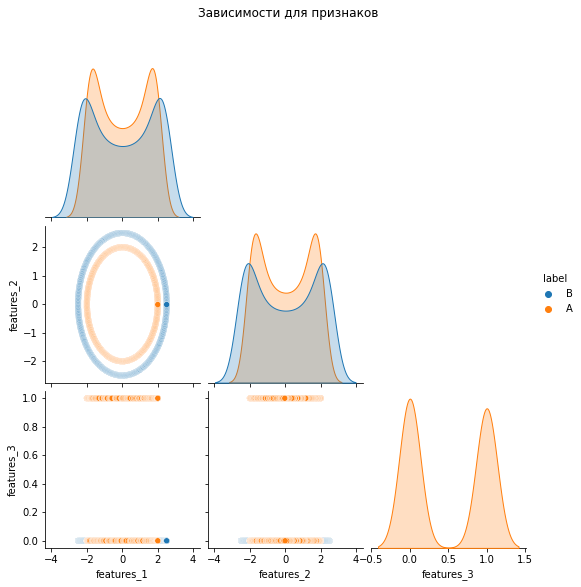
▍ Как можно решить задачу исходя из информации на графике?

Посмотрите на зависимость feature_1 и feature_2, можно ли что-то заметить? На этом графике классы хорошо разделимы окружностью. Мы имеем две окружности с центром в начале координат, большая из которых относится к одному классу, а меньшая — к другому. То есть по размеру их можно линейно поделить. Размер окружности определяется её радиусом. Зная формулу окружности, можно из имеющихся признаков извлечь радиус. Вспомним формулу окружности:

где , — декартовы координаты точек окружности, — координаты её центра, — радиус. Сгенерируем новый признак, разделяющий объекты по радиусу окружности:

df['sq_r'] = (df['features_1'] ** 2 + df['features_2'] ** 2)

Посмотрим, что у нас получилось, визуализировав взаимосвязи в данных для признаков:

На графике появился признак sq_r

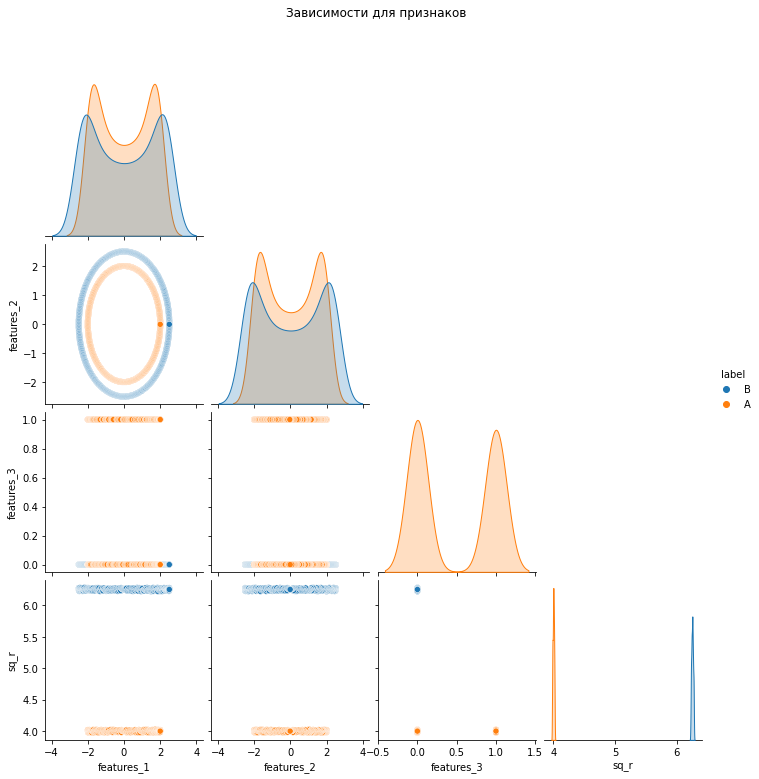
Линейная разделимость по новому признаку явная. Супер. Решим задачу с новым признаком. Остальные признаки использовать для обучения модели нецелесообразно (но некоторые из них нужны для извлечения нового признака, другой признак — некоторый шум, он нам не нужен вообще, а, впрочем, это уже совсем другая история).

Код

X = df['sq_r'].values.reshape(-1, 1)
y = df['label']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=42)
model = LogisticRegression(n_jobs=-1)
model.fit(X_train, y_train)
model.score(X_test, y_test)

Полученная точность с помощью новых признаков: 1.0

Задача решена! Справедливости ради — здесь можно использовать практически с ходу алгоритмы градиентного бустинга, но такое решение сложнее интерпретировать, а вычисления будут более затратными.

Код решения с градиентным бустингом

X = df.drop(['label', 'sq_r'], axis=1) #извлечём фичи
y = df['label'] #извлечём таргет
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=42) #отложим тестовую выборку
model = CatBoostClassifier() #модель градиентного бустинга CatBoost
model.fit(X_train, y_train, verbose=False) #отключаем визуализацию обучения
model.score(X_test, y_test)

Точность на сырых данных с помощью сильной модели: 1.0

Посмотрим на визуализацию границ классов для сильной модели:

Границы классов для алгоритма градиентного бустинга CatBoost

Задача 3 (проверь себя)

Рассмотрим более сложный случай. Загрузим данные и визуализируем их:

Над этим вариантом задачи предлагаю подумать самостоятельно, рассуждения о решении задачи можно посмотреть тут.

▍ Выводы и заключение

Алгоритмы имеют большую важность в машинном обучении, но не стоит пренебрегать и забывать про внимательную работу с данными, EDA и предобработку. Иногда именно грамотная работа с признаками, а не сложный и крутой алгоритм, может вывести вашу модель на новый уровень качества.

Статью подготовили Александр Миленькин и Сергей Комаров. Ещё больше интересных примеров вы сможете найти в наших телеграм каналах здесь и здесь.