
Для автомобилистов проблему незнакомых улиц давно решили навигаторами. Но даже автомобилисты ходят пешком. Если магазин через дорогу, то мы встаём и идём. Трудности появляются, если предстоит пройти пятьсот метров по незнакомой улице и два-три раза свернуть.
Ни один из известных нам сервисов не строил маршрут из точки А до точки Б там, где нет тропинок и тротуаров, зато полно заборов и домов причудливых очертаний.
2ГИС решил эту проблему. Мы научились строить маршруты для пешеходов по растеризованной карте местности. Карта формально представляется графом с вершинами на регулярной решётке в местах, где пешеход может находиться физически.
Принято считать, что такой способ строить маршруты неприемлем, потому что съедает много ресурсов. Под катом — как мы с этим справились.
Алгоритм
Изобразим алгоритм построения пешего маршрута.
- Растеризуем местность с разрешением 2 × 2 метра. Под растеризацию попадают дома, дороги, заборы, водоёмы, переходы, овраги… В простейшем случае каждый пиксель получает значение — можно или нельзя пройти. Но ничто не мешает градуировать проходимость:
- можно пройти быстро
- можно пройти
- проходится с трудом
- не пройти
- Рассматриваем карту местности как описание графа с неявно указанными взаимоотношениями между соседними клеточками. Переход только в проходимые, в которых мы ещё не были.
- Работаем с графом. Если ищем проход из точки в точку, используем вариант алгоритма А*.
Если ищем ближайшую дорогу, определяя проход до ближайшего из зарегистрированных объектов, то пускаем волну поиска честным алгоритмом Дейкстры.
Две вещи пугают в этой схеме: память и память. Оперативная и на диске. И та, и та расходуются слишком быстро. Попробуем решить проблему.
Боремся за оперативную память
У каждой точки потенциально 8 пар рёбер — прямое и обратное. На квадратный километр получается: 500 × 500 × 8 = 2 000 000. Если действовать «в лоб», придётся каждое обработать и сохранить…
Чтобы сэкономить оперативную память, мы делим карту на тайлы по 256 × 256 клеточек или 512 × 512 метров. Будем хранить только периметр волны, проходящий по границам тайлов. Для хранения периметра заведем общую «кучу».
Тайлы обрабатываем атомарно. При заливке тайла используем его локальную «кучу». Алгоритм такой:
- Находим тайл, в который попадает начальная точка, и вносим точку в локальную «кучу» этого тайла.
- Пускаем в тайле волну. Если при заливке мы дошли до финиша, то переходим к пункту 7. Если нет, то когда волна зальет весь тайл, на его границах мы получим длины от исходной точки.
- Заносим в общую «кучу» периметр этого тайла. Сам тайл нам больше не нужен, его можно освободить.
- Берём из общей «кучи» минимальный элемент, смотрим, в какой тайл и на какую его сторону этот элемент смотрит.
- Убираем из общей «кучи» все точки из этой стороны этого тайла и запоминаем их.
- Загружаем новый тайл. В его локальную кучу с нужной стороны заносим найденные точки. Снова возвращаемся к пункту 2.
- После того как путь найден (это фактически список точек на межтайловой решетке), восстанавливаем настоящий путь и внутри тайлов. Делаем это потому, что сами тайлы мы уже давно выгрузили для экономии памяти. Для этого мы идём по нашему пути, загружаем по очереди тайлы и заново строим маршрут, но на этот раз из точки в точку внутри тайла.
- Найденный путь выпрямляем, чтобы избавиться от характерной «пилы». Методика хоть и не устраняет все артефакты, но быстро избавляет от наиболее явных.
Для этого внутри тайла используем алгоритм Брезенхема. Для спрямления кусков пути мы рисуем между кусками линию и по маске препятствий следим, проходима ли эта линия.
Между тайлами мы также спрямляем путь. Для этого берём предпоследнюю точку предыдущего тайла и вторую текущего. Находим на решетке точку, которую заметает пересекающая их линия. В обоих тайлах Брезенхемом пытаемся пройти напрямую к этой пограничной точке. Если удалось — вуаля! — соединяем напрямую.
Посмотрим распределение стоимости внутри тайла:

Цветом — от синего к оранжевому — обозначается длина
пройденного пути. Вышли мы из правого верхнего угла.
Таким образом нам удаётся ограничиться минимумом памяти для хранения периметра волны. Даже тайлы кэшировать не обязательно. Считаем данный вариант приемлемым, а цель экономии оперативной памяти достигнутой.
Боремся за дисковую память
Для хранения одного тайла в 256 × 256 точек с разрешением в 1 бит на точку потребуется 8 килобайт. Тогда квадратный километр стоит 32 килобайта, а типичный город с окрестностями — 100 × 100 км уже весит 320 Мб.
Многовато. Но такого рода информация должна хорошо сжиматься, так как в ней присутствуют значительные перекосы в соотношении 0 и 1. Кроме того, есть длинные монотонные последовательности.
Изначально, принимая это во внимание, мы применили адаптивный арифметический кодировщик. Растеризация Новосибирска заняла около четырёх минут. Получилось 4946 непустых тайлов, которые заняли примерно 10 Мб. При этом те же данные в gif’ах занимают всего 6 Мб (что унизительно :-). Выглядит это так:

Несколько произвольных тайлов в виде картинок
10 или даже 6 Мб для Новосибирска — это больше, чем занимает наш роутинг индекс.
Кроме того, если мы будем ходить не от точки к точке, а до дороги, то потребуется ещё один растр — с дорогами, до которых может дойти пешеход. Это уже чересчур. Мы нашли другое решение — растеризация «на лету».
Растеризация «на лету»
На первый взгляд, этот подход не требует дополнительной информации. В самом деле, информация у нас уже есть: дома, заборы, дороги — всего с десяток слоёв.
Но тогда для растеризации каждого тайла придётся делать 10 пространственных запросов к пространственным индексам с последующим вычитыванием из соответствующих пространственных слоёв.
С ограничениями мобилки на доступную память, у хранилища данных почти нет кэша. Да и подсистема «чужая» — у нас нет с ней доверительных отношений, поэтому память выделяется через CRT, что не очень хорошо с точки зрения фрагментации.
Попросту говоря, такой вариант слишком дорог. Так что мы сделали своё хранилище данных для растеризации.
Для хранения геометрий используется Б-дерево с ключом из 3 элементов (или из двух + значение, если угодно):
- TileID — идентификатор тайла. Экстент карты разбивается на тайлы, нумерация идёт построчно снизу вверх слева направо.
- Attr — атрибут объекта. Используем только 1 младший бит. 0 — объект растеризуем единичками, 1 — нулями.
При траверзе дерева нули идут вперёд, и мы сначала нарисуем все блокирующие объекты (дома, заборы), а затем поверх нанесём разрешающие объекты (калитки, переезды). - Shp — геометрия, все типы геометрий упакованы вместе.
Такая организация за один поиск и один траверз находит данные данного тайла. При этом используются преимущественно стековые объекты. Дополнительная память берётся из пула, что заметно гуманнее по отношению к CRT.
Геометрии на этапе экспорта клипируются по границам тайлов. При записи дерева данные сжимаются. В результате хранение векторной информации втрое компактнее растеризованной, если сравнивать с адаптивным арифметическим кодером, и вдвое экономнее gif.
Примеры маршрутов
Идём из точки в точку, проходим через ж.-д. переезд.

Опять из точки в точку. Иногда путь пешехода в городских джунглях бывает замысловатым.
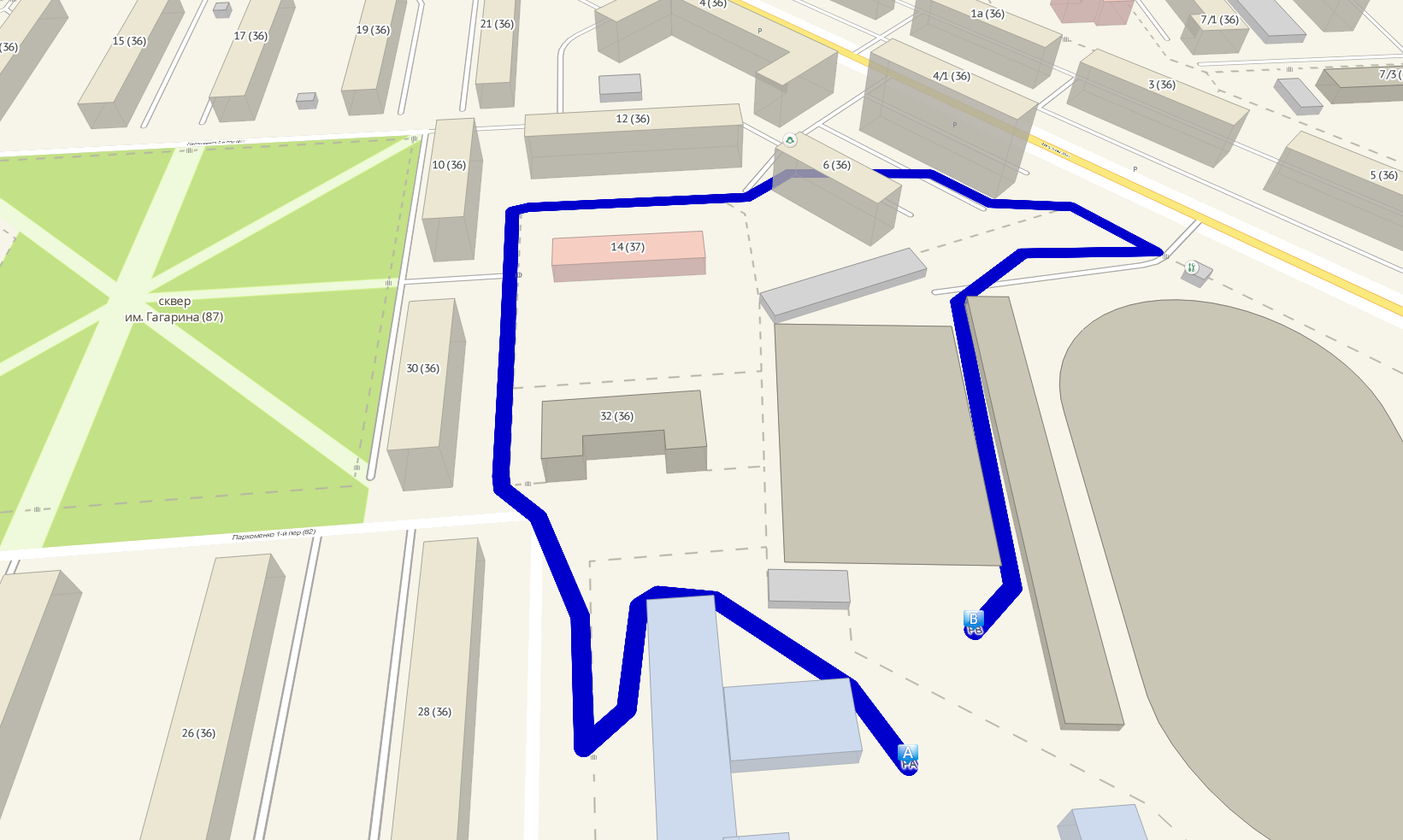
Идём до ближайшей дороги.

Опять до ближайшего ребра.
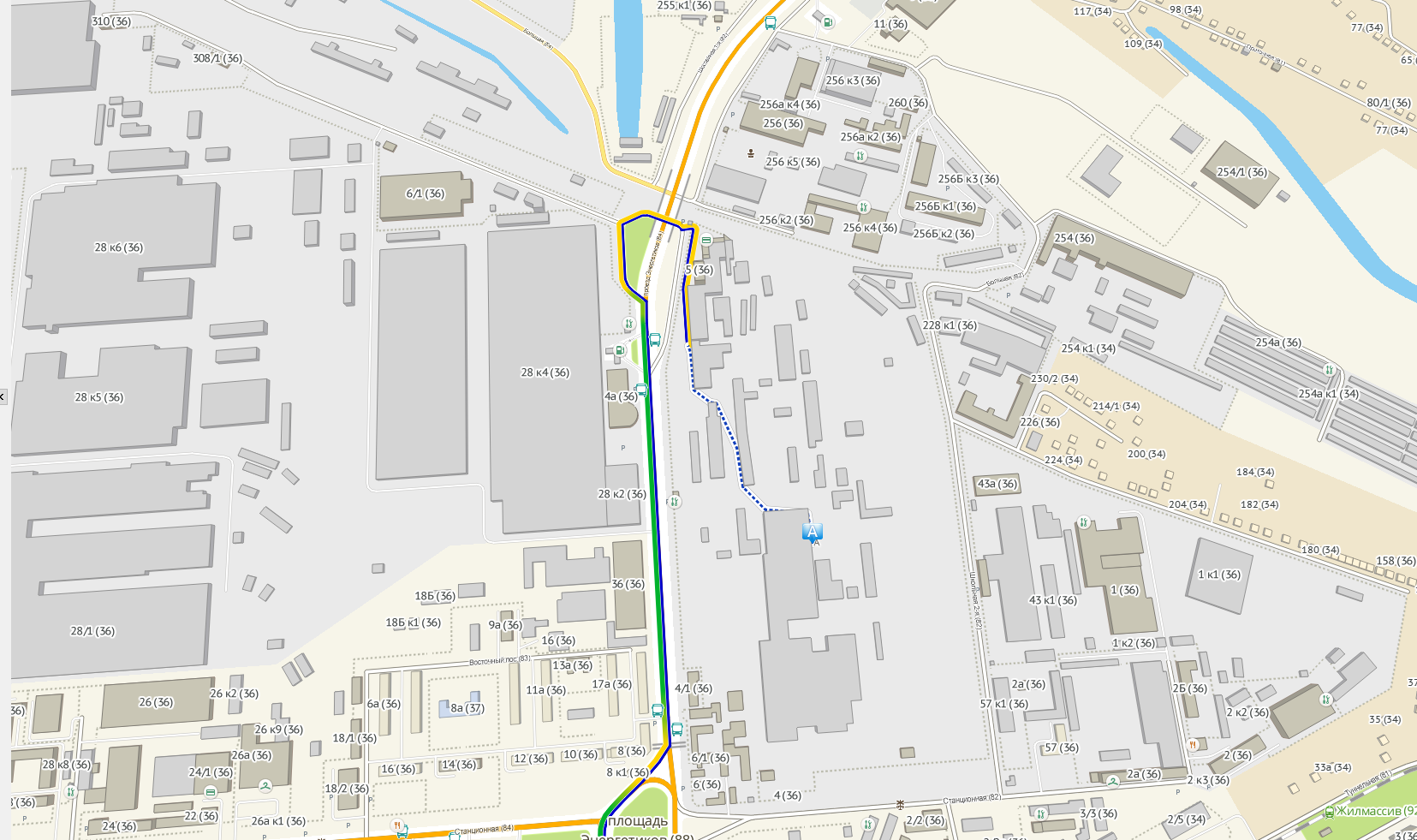
Что в итоге
Объём дополнительных данных для Новосибирска — примерно 3 Мб. Столица нашей необъятной Родины — 8Мб. Поиск за 1,5 км на десктопе занимает 90 мсек без разогрева. Это около 20 распакованных и обработанных тайлов. Дополнительной оперативной памяти, как правило, требуется меньше мегабайта.
Но у подхода есть недостатки. Несмотря на «выпрямление» геометрий, иногда результат довольно странный. Например, за счёт дискретности растеризации время от времени «слипаются» здания.
Алгоритм квадратичен к расстоянию и с этим ничего невозможно сделать. К счастью, крайне редко приходится строить на такие расстояния, когда это становится проблемой. Фактически, мы ограничиваем пеший проход двумя километрами.
И всё-таки, это лучше, чем притягиваться напрямую к ближайшим дорогам и шагать по городам и весям, невзирая на преграды. Пешие маршруты уже работают в мобильных приложениях на iOS и Windows Phone и при поиске проезда на общественном транспорте на 2gis.ru.