Методы анализа A/B тестов: как выбрать правильный метод для каждого типа метрик и размера выборки

Всем привет! Я Ваня Касторнов, продуктовый аналитик Лиги Ставок. На сегодняшний день все вокруг говорят о необходимости проведения а/б тестирования, но зачастую оказывается, что их проводят, не проверяя статистическую значимость, или даже не знают, как их проводить. Здесь не будет абстрактного описания, зачем и как делать а/б тесты, вместо этого я постараюсь развеять туман над тем, какие статистические методы использовать в разных ситуациях, а также приведу примеры скриптов на python, чтобы вы могли сразу ими воспользоваться.

Для кого эта статья: для аналитиков, продактов или любого, кто сам планирует провести аб тест.

Как читать? Я старался учесть последовательность при написании, но на самом деле, это скорее шпаргалка — в любой момент, когда вам нужно провести аб тест, вы можете найти в ней кейс, который подходит для вас, и воспользоваться им, в конце есть ссылка на сводную схему.

Пара слов, и начнем. Пока я писал эту статью, я старался не использовать много научной терминологии, чтобы не распугать вас, но где‑то она встречается, извините за это…))

Что ж, начнем…

У нас есть две выборки, которые мы получили рандомным путем. Первое, что нам нужно сделать, чтобы начать эксперимент, это определить метрику (или метрики), на основании которой мы будем принимать решение: то, на основании чего, построена сама гипотеза. Выбор статистического метода в том числе зависит от типа метрики, на которую мы будем смотреть. Мы поделим метрики на три типа:

1. Количественные (количество ставок или заказов).

2. Пропорционные или качественные (конверсия в покупку, CTR)

3. Соотношения (рентабельность или отношение открытых продуктовых карточек к количеству покупок).

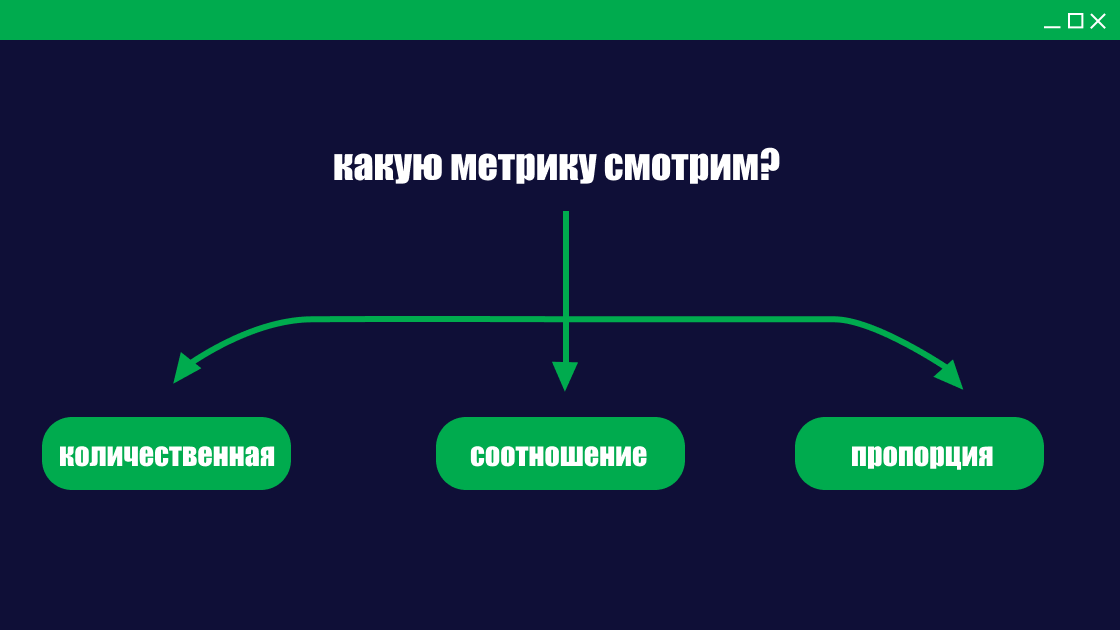
С каждым типом метрик — свой определенный подход, так как наибольшее количество А/Б тестов проводят с метриками пропорций, то с него и начнем, он же и самый простой.

Пропорции (качественные)

Тут все просто, наилучший метод чтобы проверить статистическую значимость изменения для пропорций это метод Хи‑Квадрат. Но перед тем, как его проводить, стоит проверить размер тестовой группы для желаемого минимального статистически значимого изменения. Это можно сделать, используя один из инструментов в интернете, например, этот или с помощью библиотеки statsmodels.stats через python, вот пример кода:

import statsmodels.stats.api as sms

def sample_size_calculator(baseline_rate, minimum_effect, power=0.8, alpha=0.05):

    effect_size = sms.proportion_effectsize(baseline_rate, baseline_rate + minimum_effect)
    sample_size = sms.NormalIndPower().solve_power(effect_size, power=power, alpha=alpha, ratio=1)
    return sample_size

baseline_rate = 0.10  # например, 10% конверсия в контрольной группе
minimum_effect = 0.02 # желаемо
е изменение (например, увеличение на 2%)

sample_size = sample_size_calculator(baseline_rate, minimum_effect)
print(f'Необходимый размер выборки для каждой группы: {sample_size:.0f}')

В обоих вариантах вам необходимо указать базовый уровень конверсии, минимальное значение для обнаружения изменения, уровень a (процент раз, когда разница будет обнаружена при условии, что ее нет) и уровень мощности (процент раз, когда будет обнаружено минимальное значение изменения, если оно существует).

Обнаружив необходимый размер выборки, мы можем приступать к самому тесту.

Опять же, в интернете полно сайтов с онлайн‑калькуляторами, которые позволят это сделать, например, вот этот. Если же вы решите провести тест используя python, то вот пример скрипта, который позволит это сделать.

import numpy as np
import scipy.stats as stats

# Загрузите данные в переменные
group_A = np.array([50, 100])
group_B = np.array([60, 90])

# Запустите тест
chi2, p, dof, ex = stats.chi2_contingency([group_A, group_B], correction=False)

# Рассчитайте lift и его доверительный интервал
p1 = group_B[0] / group_B.sum()
p2 = group_A[0] / group_A.sum()

# Расчет lift
lift = p1 / p2

# Расчет стандартной ошибки для lift
se_p1 = np.sqrt(p1 * (1 - p1) / group_B.sum())
se_p2 = np.sqrt(p2 * (1 - p2) / group_A.sum())
std_error = lift * np.sqrt((se_p1 / p1) ** 2 + (se_p2 / p2) ** 2)

# Доверительный интервал
ci = stats.norm.interval(0.95, loc=lift, scale=std_error)

# Выводим результаты
print("Хи-квадрат p-value: ", p)
print("Доверительный интервал изменения (lift): ", ci)

# Проверяем есть ли статистически значимое изменение
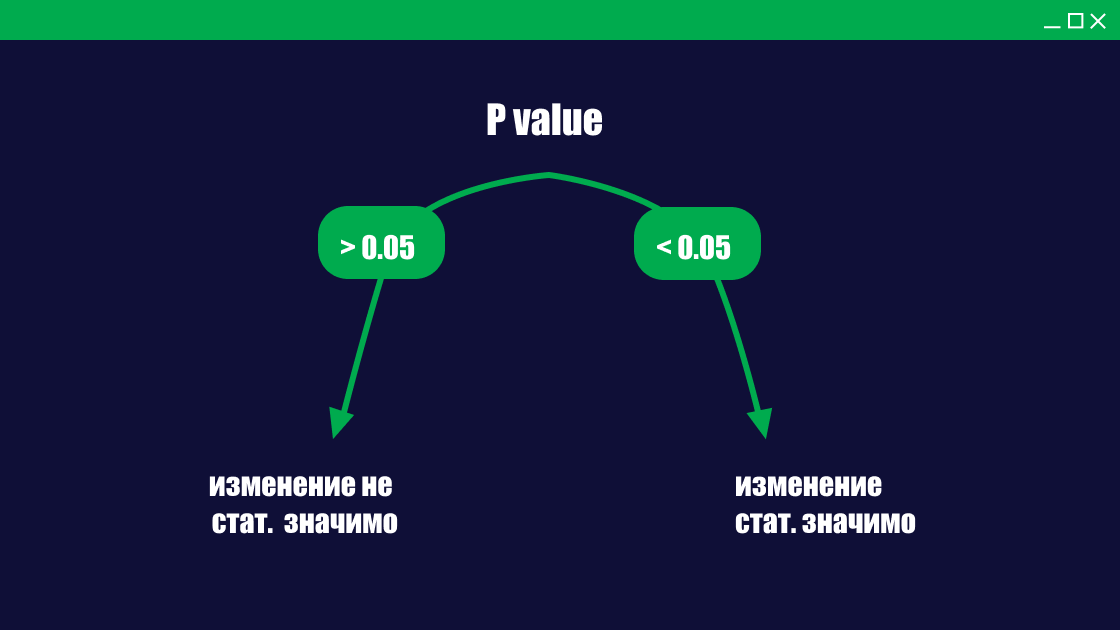
if p < 0.05 and ci[0] > 1:
    print("Вариант B лучше.")
elif p < 0.05 and ci[1] < 1:
    print("Вариант A лучше.")
else:
    print("Статистически значимой разницы нет.")

Количественные

Вторые по популярности аб тесты проходят с количественными метриками, примерами таких метрик могут быть: количество ставок, длина сессии и тд. При анализе количественных метрик важно выбрать правильный метод проверки статистической значимости. Так как мы выбрали рандомизированный метод сплитования, то скорее всего мы столкнемся с высоким уровнем дисперсии (разности) данных, что будет негативно влиять на определение значимости результатов, поэтому я рекомендую использовать CUPED (Controlled pre‑post experimental design) — это статистический метод, который все чаще используется в А/Б тестировании для повышения точности полученных результатов.

Таким образом, мы сможем нивелировать уровень дисперсии, сезонные изменения, маркетинговые акции и другие факторы. Подробнее про метод вы можете почитать тут или в оригинальной статье.

Для того, чтобы использовать cuped, нам потребуются набор данных со значением метрик в предтестовый период и само значение в момент теста. Для того, чтобы преобразовать данные вот пример скрипта:

# Рассчитываем среднее и дисперсию предтестовой метрики
mean_pre_test = df['pre_test_metric'].mean()
var_pre_test = df['pre_test_metric'].var()

# Рассчитываем ковариацию между предтестовой и тестовой метрикой
cov = df[['pre_test_metric', 'test_metric']].cov().iloc[0, 1]

# Вычисляем коэффициент theta
theta = cov / var_pre_test

# Применяем CUPED
df['cuped_metric'] = df['test_metric'] - theta * (df['pre_test_metric'] - mean_pre_test)

После того, как мы получили данные, стоит оценить размер выборки, тут есть два варианта.

Если выборка большая…

То нужно посмотреть на нормальность распределения данных, в целом все просто, проверить нормальность распределения поможет вот этот скрипт, который использует тест Шапиро‑Уилка, он подойдет в большинстве случаев, кроме очень больших выборок, так как он может стать чувствительным к незначительным отклонениям от нормальности:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import shapiro, norm

# Загрузка данных
data = pd.read_csv('adjusted_experiment_data.csv')
# Предположим, что анализируемый столбец называется 'metric'
metric_data = data['metric']

# Применяем тест Шапиро-Уилка
stat, p = shapiro(metric_data)

alpha = 0.05
if p > alpha:
    print("Нормальное распределение.")
else:
    print("Не нормальное распределение.")

# График с распределением
fig, ax = plt.subplots()
ax.hist(metric_data, bins=30, density=True, alpha=0.5, label='Data')  # Изменил bins на 30 для более детального графика

mu, std = norm.fit(metric_data)
xmin, xmax = ax.get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
ax.plot(x, p, 'k', linewidth=2, label='Normal distribution')
ax.legend()
plt.show()

Итак, распределение получилось нормальным, что же дальше..

Дальше мы можем провести самый используемый метод проверки отсутствия нулевой гипотезы, а именно t‑test, наиболее известным является т‑критерий стъюдента, он также подойдет, если же между группами осталась неравная дисперсия, то лучше подойдет т‑критерий Уэлча, в целом может использовать его всегда не будет ошибкой, но вы можете столкнуться с меньшим уровнем значимости. Оба теста удобно проводить, используя библиотеку scipy.stats, вот примеры кодов:

import pandas as pd
import scipy.stats as stats

data = pd.read_csv('adjusted_experiment_data.csv')

control = data[data['group_type'] == 'control']['experiment_data']
test = data[data['group_type'] == 'test']['experiment_data']

# т-критерий Уэлча
welch_t, welch_p = stats.ttest_ind(control, test, equal_var=False)

# т-критерий Стъюдента
student_t, student_p = stats.ttest_ind(control, test, equal_var=True)


print("Welch's t-test:")
print("t-statistic: ", welch_t)
print("p-value: ", welch_p)

print("\nStudent's t-test:")
print("t-statistic: ", student_t)
print("p-value: ", student_p)

Что делать, если размер выборки нормальный, мы разобрались, но бывает, когда данных очень мало или распределение не нормальное, тут на помощь приходит bootstrap. Основная идея bootstrap заключается в многократной выборке с заменой из исходных данных для создания большого количества «выборок». Каждая выборка похожа на исходную выборку, но имеет немного другие значения из‑за случайного подставления, подробнее можно узнать в этой статье, а пример скрипта выглядит так:

import numpy as np
import pandas as pd
from scipy.stats import mannwhitneyu
from scipy.stats import ttest_ind
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns

from tqdm.auto import tqdm
import seaborn as sns

plt.style.use('ggplot')
def get_bootstrap(
    data_column_1, # числовые значения первой выборки
    data_column_2, # числовые значения второй выборки
    boot_it = 1000, # количество бутстрэп-подвыборок
    statistic = np.mean, # интересующая нас статистика
    bootstrap_conf_level = 0.95 # уровень значимости
):
    boot_len = max([len(data_column_1), len(data_column_2)])
    boot_data = []
    for i in tqdm(range(boot_it)): # извлекаем подвыборки
        samples_1 = data_column_1.sample(
            boot_len, 
            replace = True # параметр возвращения
        ).values
        
        samples_2 = data_column_2.sample(
            boot_len, # чтобы сохранить дисперсию, берем такой же размер выборки
            replace = True
        ).values
        
        boot_data.append(statistic(samples_1-samples_2)) 
    pd_boot_data = pd.DataFrame(boot_data)
        
    left_quant = (1 - bootstrap_conf_level)/2
    right_quant = 1 - (1 - bootstrap_conf_level) / 2
    quants = pd_boot_data.quantile([left_quant, right_quant])
        
    p_1 = norm.cdf(
        x = 0, 
        loc = np.mean(boot_data), 
        scale = np.std(boot_data)
    )
    p_2 = norm.cdf(
        x = 0, 
        loc = -np.mean(boot_data), 
        scale = np.std(boot_data)
    )
    p_value = min(p_1, p_2) * 2
        
    # Визуализация
    _, _, bars = plt.hist(pd_boot_data[0], bins = 50)
    for bar in bars:
        if abs(bar.get_x()) <= quants.iloc[0][0] or abs(bar.get_x()) >= quants.iloc[1][0]:
            bar.set_facecolor('red')
        else: 
            bar.set_facecolor('grey')
            bar.set_edgecolor('black')
    
    plt.style.use('ggplot')
    plt.vlines(quants,ymin=0,ymax=50,linestyle='--')
    plt.xlabel('boot_data')
    plt.ylabel('frequency')
    plt.title("Histogram of boot_data")
    plt.show()
       
    return {"boot_data": boot_data, 
            "quants": quants, 
            "p_value": p_value}

Фух, кажется с количественными метриками все…

Соотношения

В соотношениях два числовых значения, чаще всего числитель — это количество выполненных действий, а знаменатель — это количество пользователей, например, количество ставок на пользователей, которые открывали карточки событий, или же количество открытых карточек на количество просмотренных. Бывает, что суть гипотезы именно в изменении подобных метрик, что ж, тут мы будем ориентироваться на два варианта проверки статистической значимости, которые основываются на размерах выборки.

Большая выборка

Тест Стьюдента не работает для метрик отношения из-за зависимых данных. Одна из причин этого — неправильная оценка дисперсии для таких типов данных.

Тест Стьюдента обычно предполагает, что данные независимы и одинаково распределены, и основывается на выборочной дисперсии для оценки стандартной ошибки среднего. Однако, когда данные зависимы или когда рассматривается метрика отношения (например, конверсия, где число успехов делится на общее число попыток), такие предположения могут быть нарушены, и стандартные методы оценки дисперсии могут давать смещенные результаты. Тут на помощь нам приходит Дельта-метод. Давайте представим простой пример. У вас есть куча данных, и вы хотите сделать с ними что-то сложное, например, посчитать средний доход на одного клиента, деление общего дохода на количество клиентов. Когда вы делаете такие операции, ваши данные меняются, и с ними меняется и точность, с которой мы можем оценить результат. Дельта-метод — это способ посчитать, насколько точными остаются ваши данные после всех этих операций. Проще говоря, это метод, который помогает понять, насколько можно доверять результату ваших расчетов, когда вы делаете что-то сложное с исходными данными.

import numpy as np
import scipy.stats as stats

def delta_method_test(control_data, test_data):
    # Расчет основных статистик для каждой группы
    mean_control = np.mean(control_data)
    mean_test = np.mean(test_data)
    var_control = np.var(control_data, ddof=1)
    var_test = np.var(test_data, ddof=1)
    n_control = len(control_data)
    n_test = len(test_data)

    # Расчет общей дисперсии
    combined_var = var_control / n_control + var_test / n_test

    # Расчет разности средних
    mean_diff = mean_test - mean_control

    # Расчет t-статистики
    t_stat = mean_diff / np.sqrt(combined_var)

    # Расчет p-value
    p_value = 2 * (1 - stats.norm.cdf(np.abs(t_stat)))

    return p_value

control_group = np.array([данные контрольной группы])
test_group = np.array([данные тестовой группы])
p_value = delta_method_test(control_group, test_group)

print(f"P-value: {p_value}")

Маленькая выборка

Ну и последний метод, который мы рассмотрим, который стоит применять если размер выборки маленький. В таком случае bootstrap будет также актуален. Но так как мы пытаемся анализировать метрику, соотношения и наблюдения в данных могут быть независимыми, то больше подойдет блочный bootstrap. В обычном bootstrap данные берутся из исходной выборки с заменой, в блочном данные берутся группами (или блоками). Это нужно потому, что мы хотим учесть структуру зависимости в данных. В конце проведем уже известным нам t‑test.

Скрипт похож на обычный bootstrap:

import pandas as pd
import numpy as np
import scipy.stats as stats

data = pd.read_csv('output.csv')

control = data[data['group'] == 'control']
treatment = data[data['group'] == 'test']

observed_effect = treatment['after'].mean() - control['after'].mean()

# определяем количество блоков
num_blocks = 100
block_size = len(data) // num_blocks

bootstrap_samples = []
for i in range(num_blocks):
    # вставляем данные в блоки
    block_indices = np.random.choice(range(len(data)), size=block_size, replace=True)
    bootstrap_sample = data.iloc[block_indices]

    # сплитуем по группам
    bootstrap_control = bootstrap_sample[bootstrap_sample['group'] == 'control']
    bootstrap_test = bootstrap_sample[bootstrap_sample['group'] == 'test']

    # считаем эффект через bootstrap
    bootstrap_effect = bootstrap_test['after'].mean() - bootstrap_control['after'].mean()

    bootstrap_samples.append(bootstrap_effect)

# стандартная ошибка bootstrap
bootstrap_std_err = np.std(bootstrap_samples)

# проводим t-test
t_statistic = observed_effect / bootstrap_std_err
p_value = stats.t.sf(np.abs(t_statistic), len(data) - 1) * 2

print("Observed treatment effect: ", observed_effect)
print("Bootstrap estimate of standard error: ", bootstrap_std_err)
print("t-statistic: ", t_statistic)
print("p-value: ", p_value)

Вывод

В итоге, чтобы провести успешный A/B тест, необходимо выбрать метод анализа, который подходит для конкретных метрик и размера выборки, а также учитывать все факторы, которые могут повлиять на результаты. Важно следить за мощностью эксперимента после его проведения, чтобы убедиться, что результаты являются значимыми.

Для более простого восприятия я добавил в Miro общую схему, которая будет работать как навигатор выбора стат метода для вашего теста.

Я надеюсь, что эта статья поможет вам в проведении А\Б тестов и увеличит значимость принимаемых решений, что положительно отразится на вашем продукте и личном прогрессе.

Подписывайтесь на мой телеграм канал, где я рассказываю как улучшать продукты на основе анализа данных, а также добавляйте статью в избранное, и до скорой встречи!