Алгоритмы *

— Указатели в СтарБейсике видишь?
— …
— А они там есть.

Математический анализ знает множество замечательных функций со своими удивительными свойствами и применениями. Сегодня я бы хотел рассказать читателю об одной из таких - W-функции Ламберта.

Чтобы уверенно пересечь незнакомую местность, можно или двигаться быстрее, или подыскивать удобную дорожку. Другими словами, слишком пристальное внимание к скорости как таковой может вас притормозить. То же касается и разработки программного обеспечения.

Я очень люблю скелетные детекторы из Mediapipe. Чтобы запустить их нужно всего несколько минут. Работает на разных платформах (мобильные, pc, embedded, и.т.д.). И выдает достаточное качество для многих применений. 

Но надо признать что не всюду его можно брать и использовать. Давайте я расскажу как небольшими силами можно его улучшить. Приведенная тут логика будет построена вокруг Mediapipe, но она им не ограничена. Применяя аналогичные подходы можно улучшить практически любой скелетный алгоритм.

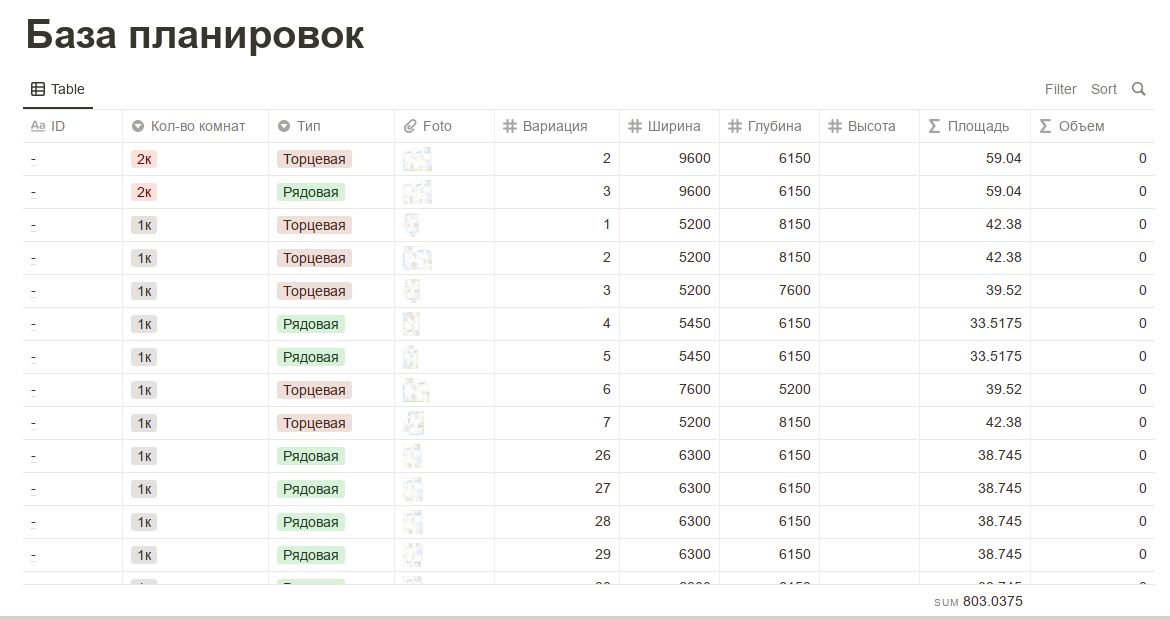
Предложенный алгоритм - это очень ранний прототип рабочей версии. Суть публикации познакомить всех желающих с возможностями генетических алгоритмов в различных сферах бизнеса.

Любому блокчейн-проекту, который рассчитывает на успех, стоит думать, что он будет с этим успехом делать. Больше пользователей, больше транзакций, больше нагрузка на сеть — рано или поздно встанет вопрос о масштабировании. В этом посте мы расскажем, куда нас привели вопросы масштабирования, согласованности и почему мы не взяли на вооружение какой-нибудь готовый консенсус.

Привет, Хабр! На связи команда направления прогнозирования промо в «Магните». В предыдущей статье «Магнитная аномалия: как предсказать продажи промо в ритейле» мы дали читателю общее представление о том, чем занимается наша команда. Теперь поговорим о конкретных сложностях и методах их решения, с которыми нам приходится сталкиваться в работе.

Чтобы лучше разобраться во внутренней кухне, предлагаем читателю вместе прогуляться по нашим «девяти кругам прогнозирования промо спроса».

Грокаем алгоритмы. Иллюстрированное пособие для программистов и любопытствующих от Бхаргава А. Эта книга рекомендована Яндекс Практикум при подготовке к алгоритмическому собеседованию. Сам автор указывает, что книга для самоучек, студентов, выпускников и тех, у кого программирование не является основным профилем.

Мое впечатление неоднозначно. С одной стороны, до сего момента я не встречал описания динамического программирования, поиска кратчайшего пути в графе по алгоритму Дейкстры и использование K ближайших соседей для классификации и аппроксимации (возможно, все это есть в 4^м или последующих томах Кнута, но в магазине они мне не встречались). С другой стороны, описания и примеры, приведенные в книге, таковы, что практической пользы не представляют. Описания очень поверхностны, примеры нарочно примитивны, код в половине случаев не приведен. Но даже там где есть код, он нарочито упрощен под конкретный пример и на практике бесполезен.

Казалось бы, есть масса книг - каталогов шаблонов. Они реально полезны и новичку и профессионалу. Эта книга не из их числа. Но, видимо, это и не было целью. Напоминает научно-популярные книги издававшиеся в СССР: простым языком рассказывает о сложных вещах, прививает у читателя интерес к теме, расширяет кругозор. Не более. Но тоже важно.

Вернемся к Яндекс Практикум и их рекомендации. Если алгоритмы так важны, то почему именно эта книга? Есть масса других, где и алгоритмов больше и разобраны они так, что бери да пользуй. Например, классический труд Д. Э. Кнута Искусство программирования. Да, рисунки в детском стиле в Грокаем алгоритмы забавны. Но иллюстрации в Искусство программирования полезны для понимания. Разве это не важнее, если уж кандидата посылают на алгоритмическое собеседование?

Пара слов о том, что мы будем изучать.

Как я оптимизировал аналитику используя структуры данных. Что в итоге сэкономило $22 000

Двое молодых математиков ошеломили коллег, представив полное доказательство гипотезы Кана-Калаи — обобщающее утверждение о том, как возникает структура в случайных множествах и графах.

Когда математики Джефф Кан и Гиль Калаи в 2006 году впервые выдвинули свою гипотезу о «пороге ожидания», они сами в нее не поверили. Их тезис – широкое утверждение о природе математических объектов, именуемых «случайными графами» — казался слишком категоричным, слишком всеобъемлющим, слишком смелым, чтобы претендовать на истинность. Казалось, что он скорее выдает желаемое за действительное, чем отражает математическую истину. Даже с такими оговорками, никто не смог опровергнуть эту гипотезу, и она быстро стала одной из важнейших нерешенных задач в своей области.

Теперь, более 15 лет спустя, двое молодых математиков из Стэнфордского университета сделали то, что, по мнению Кана и Калаи, граничит с невозможным. В В на удивление кратком препринте, выложенном в онлайне всего несколько недель назад, Джинён Пак и Гью Туан Фам дали полное доказательство этой гипотезы.

«Оно получилось поразительно простым и изобретательным», —  сказал Калаи, —  «Завораживающим. Чудесным».

Привет, меня зовут Петр и я работаю в Badoo в команде биллинга. В этой статье я хочу поделиться своим опытом работы над пет-проектом по созданию хранилища фотографий с возможностью поиска дубликатов. Я расскажу, с каким багажом я вошел в этот проект, в чем заключалась задача и как её решал. В конце поделюсь результатами и почему я считаю, что это один из лучших проектов, которым я занимался. 

Однажды мои знакомые попросили сделать им хранилище изображений для их проекта по модерации внешних ресурсов. Условия: срок хранения до трех лет, фотографии при этом присылаются неравномерно, в среднем поток — 150.000 картинок в сутки.

Казалось бы, достаточно банальная задача. Если бы не еще одно условие: хорошо бы сопоставлять фотографии с уже имеющимися: искать дубликаты и помечать их. 

Сегодня мы разберем хитроумный и нетривиальный алгоритм поиска подстроки в строке. Он основан не на сравнении символов, а на сравнении чисел. Я уже писал, что основная моя цель это не написать простой разбор алгоритмов, а посмотреть их эффективность, какие-то интересные места и сравнить их производительность между собой.
И сегодня есть что посмотреть.

В декабре 2021 года Github объявил, что открывает общий доступ к точной навигации по коду для всех публичных и приватных репозиториев с Python на сайте GitHub.com. Точную навигацию в коде обеспечивают стековые графы, новый фреймвввооорк с открытым исходным кодом, созданный в Github и позволяющий устанавливать правила привязки имен для языка программирования при помощи декларативного предметно-ориентированного языка (DSL). Стековые графы позволяют генерировать данные о навигации по стеку для конкретного репозитория, не требуя при этом какого-либо участия в конфигурировании со стороны владельца репозитория и не вмешиваясь в процесс сборки или другие задания, связанные с непрерывной интеграцией. В этом посте будет подробно рассказано, как работают стековые графы, и как с их помощью достигаются такие результаты.

(Этот пост написан на основе доклада, прочитанного автором на конференции Strange Loop в октябре 2021 года. Есть видео с этим докладом, там рассказано гораздо больше!)

О чем и для кого эта книга

Много воды утекло с тех пор, как я в последний раз участвовал в собеседовании по программированию как соискатель. Но до сих пор помню особенно полюбившийся мне вопрос с такого собеседования. Дело было в MemSQL, году так в 2013. (Они даже успели переименоваться, поэтому, полагаю, конкретно этот вопрос они на собеседовании уже не задают. Не чувствую вины за то, что выдаю его. Это отличная история, которая также кажется мне поучительной; просто раньше я о ней никогда не писал).

Окей, вообще, это даже не вопрос как таковой, это программерская задачка на засыпку. Не помню, сколько времени мне на нее дали. Скажем, три часа, считая время, потребовавшееся на постановку задачи.

Поскольку компания MemSQL разрабатывала базу данных, этот челлендж из той же оперы.

Какой консенсус лучше для блокчейна, proof-of-work или proof-of-stake? Многие спорят об этом и приводят разные аргументы. В этой статье я рассмотрю основные преимущества и недостатки каждого варианта.

Это перевод поста из блога Bitcoin, дополненный комментариями наших экспертов. Эти комментарии выделены курсивом.

Написав предыдущую статью о сортировке подсчётом beSort - меня не отпустило. Я решил поковыряться в базовых алгоритмах и залип на модификациях пузырьковой сортировки, ну а статья о том - что из этого получилось.

Всем привет! Если перед вами стоит задача проведения А/Б тестирования, то я помогу вам понять, как с помощью python сформировать однородные группы с помощью алгоритмов сходства объектов на основе косинусного и взвешенного косинусного расстояния для его проведения.

Любое натуральное число можно выразить через уникальное множество простых чисел, перемножение которых даёт исходное число. Для простых чисел это множество состоит из одного элемента – самого этого числа. Такую композицию можно называть мультипликативной, она очень хорошо известна и изучена.

В статье предлагается способ выразить натуральное число через уникальное множество простых чисел (включая единицу), сложение которых даёт исходное число. Такую композицию будем называть аддитивной, и она ранее не предлагалась.

При работе над статьёй была посчитана композиция чисел до одного триллиона. Данный расчёт дал довольно интересные результаты, изложенные в статье. Возможно, обсуждение этих результатов поможет сделать дальнейшие выводы, пригодные для публикации в научном журнале.