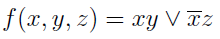В этой статье я расскажу про достаточно важную в информатике и теории автоматов тему – минимизацию булевых функций. Этим вопросом задавались пожалуй все, кто изучал или сталкивался с данной тематикой.
Существует немало методов, однако наибольший интерес представляют те, которые могут быть формализованы, а соответственно запрограммированы без особых сложностей. А также работающие с произвольными булевыми выражениями. Идеального метода не придумано, все имеют те или иные слабые и сильные качества. Я остановлюсь на так называемом методе Гиперкубов — Методе Квайна.
Метод, к сожалению, применим только для Совершенных ДНФ, поэтому при большом числе переменных использование затруднено гигантским выражением СДНФ.
Метод заключается в применении известных правил Склеивания и поглощения.
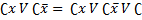

Перед описанием алгоритма объясню почему метод называется методом гиперкубов.
Возьмем произвольную функцию f, M1(f) – единичное множество. Проще говоря, множество наборов переменныx, на которых функция обращается в верное высказывание.
Гиперкуб – это множество M1(f).
Коньюнктивный одночлен – импликанта, если М1(K) входит в M1(f).
Импликанту называют простой, если не существует другого K2, что M1(K) содержится в M1(K2), говоря простым языком – соответствует самому большому гиперкубу.
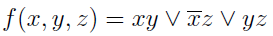
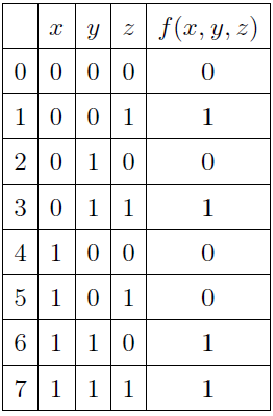
Построим таблицу истинности для нее:
Выпишем все гиперкубы, лежащие в M1(f) и соответствующие им импликанты:

Выбираем простые импликанты и строим таблицу их накрытия:
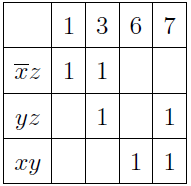
Поскольку импликанта yz перекрывается другими, ее можно изъять из выражения. Выходит, что тупиковая ДНФ функции имеет вид:
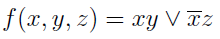
Существует немало методов, однако наибольший интерес представляют те, которые могут быть формализованы, а соответственно запрограммированы без особых сложностей. А также работающие с произвольными булевыми выражениями. Идеального метода не придумано, все имеют те или иные слабые и сильные качества. Я остановлюсь на так называемом методе Гиперкубов — Методе Квайна.
Метод, к сожалению, применим только для Совершенных ДНФ, поэтому при большом числе переменных использование затруднено гигантским выражением СДНФ.
Метод заключается в применении известных правил Склеивания и поглощения.
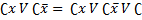

Перед описанием алгоритма объясню почему метод называется методом гиперкубов.
Возьмем произвольную функцию f, M1(f) – единичное множество. Проще говоря, множество наборов переменныx, на которых функция обращается в верное высказывание.
Гиперкуб – это множество M1(f).
Коньюнктивный одночлен – импликанта, если М1(K) входит в M1(f).
Импликанту называют простой, если не существует другого K2, что M1(K) содержится в M1(K2), говоря простым языком – соответствует самому большому гиперкубу.
Основные этапы данного метода
- Построить таблицу истинности.
- Выписать все гиперкубы из M1(f) и импликанты.
- Взять простые импликанты.
- Построить таблицу накрытия.
- Из оставшихся простых импликантов создать тупиковую ДНФ.
Возьмем в качестве примера следующую булеву функцию.
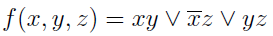
Построим таблицу истинности для нее:

Выпишем все гиперкубы, лежащие в M1(f) и соответствующие им импликанты:

Выбираем простые импликанты и строим таблицу их накрытия:

Поскольку импликанта yz перекрывается другими, ее можно изъять из выражения. Выходит, что тупиковая ДНФ функции имеет вид: