Именно о лесенках хотелось бы немного поговорить. Есть такая относительно распространенная задача с программистских собеседований:
Вы поднимаетесь по лестнице. На каждом шаге вы можете подняться либо на 1 ступеньку, либо на 2. Всего лестница имеет n ступенек. Сколькими разными способами вы можете дойти до конца лестницы?
Задача не сильно сложная, но имеющая пару интересных моментов относительно минимально возможной сложности решения и демонстрирующая «штуки, которые интересно знать».
Очевидно, что так или иначе решение начинается с наблюдения, что на каждом шаге у нас есть выбор из двух действий: сделать один шаг или сделать два шага. В первом случае лестница уменьшается на одну ступеньку, во втором — на две. Общее количество возможных способов обойти лестницу равно сумме количества способов сделать это, если мы начинаем с одной ступеньки, и количества способов, если начинаем с двух. В итоге решение сводится к рекуррентной формуле:
F(n) = F(n-1) + F(n-2)
Рекурсивная или итеративная реализация данного алгоритма «в лоб» выглядит ненамного длиннее самого соотношения (проблему переполнения оставляем за скобками):
Само по себе это решение верное, но его эффективность низка: алгоритм экспоненциален. Сложность можно уменьшить, воспользовавшись стандартной техникой динамического программирования — мемоизацией. Интуитивное объяснение: с каждой конкретной ступеньки на лестнице количество способов дойти до конца не зависит от того, как мы попали на эту ступеньку, поэтому ответ имеет смысл запомнить и использовать на следующих шагах расчета. Код приводить не буду — главное, что вкупе с итерацией получается линейное решение. Однако это не все.
Внимательный читатель заметит, что соотношение выше является попросту формулой чисел Фибоначчи с поправкой n на единицу (поправка появляется из-за того, что начальные условия другие — Fib(0) = 0, Fib(1) = 1, Fib(2) = 1, а в нашем случае лесенки F(0) = 1, F(1) = 1, F(2) = 2). Известно, что для чисел Фибоначчи имеет место следующее соотношение:
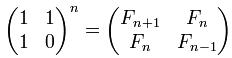
Таким образом, после данного возведения в степень результирующая матрица будет содержать интересующее нас «n+1»-ое число Фибоначчи в первом столбце первой строки (элементы матриц традиционно индексирую с единицы).
Сам по себе этот факт уже интересен, однако особенно интересен он в сочетании с алгоритмом быстрого возведения в степень. Применительно к нашей задаче это означает, что мы можем получить ответ за O(ln N) умножений. Код этого решения на языке Python (опять же, чтобы забыть пока про проблему переполнения — Python автоматически переключается на использование big integer, когда это надо) выглядит так:
Собственно, все. Надеюсь, как и я, читатель испытывает удовлетворение от осознания факта, что лестницу длиной в 200 ступенек можно прошагать в соответствии с условиями задачи 453973694165307953197296969697410619233826-ю разными способами.И что это может быть подсчитано с логарифмической сложностью.
UPDATE: по итогам чтения комментариев спешу сделать пару замечаний:
Вы поднимаетесь по лестнице. На каждом шаге вы можете подняться либо на 1 ступеньку, либо на 2. Всего лестница имеет n ступенек. Сколькими разными способами вы можете дойти до конца лестницы?
Задача не сильно сложная, но имеющая пару интересных моментов относительно минимально возможной сложности решения и демонстрирующая «штуки, которые интересно знать».
Очевидно, что так или иначе решение начинается с наблюдения, что на каждом шаге у нас есть выбор из двух действий: сделать один шаг или сделать два шага. В первом случае лестница уменьшается на одну ступеньку, во втором — на две. Общее количество возможных способов обойти лестницу равно сумме количества способов сделать это, если мы начинаем с одной ступеньки, и количества способов, если начинаем с двух. В итоге решение сводится к рекуррентной формуле:
F(n) = F(n-1) + F(n-2)
Рекурсивная или итеративная реализация данного алгоритма «в лоб» выглядит ненамного длиннее самого соотношения (проблему переполнения оставляем за скобками):
int f(int n)
{
if (n == 0 || n == 1) return 1;
return f(n-1) + f(n-2);
}
Само по себе это решение верное, но его эффективность низка: алгоритм экспоненциален. Сложность можно уменьшить, воспользовавшись стандартной техникой динамического программирования — мемоизацией. Интуитивное объяснение: с каждой конкретной ступеньки на лестнице количество способов дойти до конца не зависит от того, как мы попали на эту ступеньку, поэтому ответ имеет смысл запомнить и использовать на следующих шагах расчета. Код приводить не буду — главное, что вкупе с итерацией получается линейное решение. Однако это не все.
Внимательный читатель заметит, что соотношение выше является попросту формулой чисел Фибоначчи с поправкой n на единицу (поправка появляется из-за того, что начальные условия другие — Fib(0) = 0, Fib(1) = 1, Fib(2) = 1, а в нашем случае лесенки F(0) = 1, F(1) = 1, F(2) = 2). Известно, что для чисел Фибоначчи имеет место следующее соотношение:
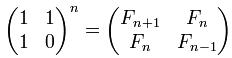
Таким образом, после данного возведения в степень результирующая матрица будет содержать интересующее нас «n+1»-ое число Фибоначчи в первом столбце первой строки (элементы матриц традиционно индексирую с единицы).
Сам по себе этот факт уже интересен, однако особенно интересен он в сочетании с алгоритмом быстрого возведения в степень. Применительно к нашей задаче это означает, что мы можем получить ответ за O(ln N) умножений. Код этого решения на языке Python (опять же, чтобы забыть пока про проблему переполнения — Python автоматически переключается на использование big integer, когда это надо) выглядит так:
#!/usr/bin/env python
# You are climbing a stair case. Each time you can either make 1 step or 2
# steps. The staircase has n steps. In how many distinct ways can you climb the
# staircase?
def mul(a, b):
return ((a[0][0] * b[0][0] + a[0][1] * b[1][0],
a[0][0] * b[0][1] + a[0][1] * b[1][1]),
(a[1][0] * b[0][0] + a[1][1] * b[1][0],
a[1][0] * b[0][1] + a[1][1] * b[1][1]))
def pow(a, N):
"""Fast matrix exponentiation"""
assert N >= 1
if N == 1:
return a
x = pow(a, N / 2)
ret = mul(x, x)
if N % 2:
ret = mul(ret, a)
return ret
def num_stair_ways(N):
x = pow(((1, 1), (1, 0)), N)
return x[0][0]
for i in range(1, 1001):
print i, num_stair_ways(i)
Собственно, все. Надеюсь, как и я, читатель испытывает удовлетворение от осознания факта, что лестницу длиной в 200 ступенек можно прошагать в соответствии с условиями задачи 453973694165307953197296969697410619233826-ю разными способами.
UPDATE: по итогам чтения комментариев спешу сделать пару замечаний:
- Недавно уже была статья на очень похожую тему. Статья имеет много дельных комментариев. Было бы недурно на хабре иметь автоматический поиск сходных статей при обубликовании.
- Все рассуждения про алгоритмы вычисления N-го члена экспоненциально растущей последовательности за O(ln N) операций должны принимать во внимание линейно растущую разрядность чисел. То есть, количество умножений может расти как O(ln N), но сложность каждого отдельно взятого умножения будет все же расти линейно от N. Поэтому общая сложность может оставаться логарифмической, только если достаточно нахождения финального значения по какому-либо модулю.