В данной статье речь пойдет об алгоритме HEngine и реализации решения проблемы подсчета расстояния Хэмминга на больших объемах данных.
Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.
Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.
Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.
Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.
Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.
Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.
Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.
В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.
— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.
В статье описывается решение только статической задачи.
Данная реализация фокусируется на поиске строк в пределах k <= 10.
Существует три решения статической задачи: линейный поиск (linear scan), расширение запроса (query expansion) и расширение базы данных (table expansion).
В данном случае под расширением запроса имеется в виду генерация всех возможных вариантов строк, которые вписываются в заданное расстояние для первоначальной строки.
Расширение базы данных подразумевает создание множества копий этой базы данных, где или также генерируются все возможные варианты, которые отвечают требованиям необходимого расстояния, либо данные обрабатываются каким-то другим способом (подробно об этом чуть дальше.).
HEngine [8] использует комбинацию этих трех методов для эффективного балансирования между памятью и временем исполнения.
Алгоритм базируется на небольшой теореме, которая гласит следующее:
Если для двух строк a и b расстояние HD( a, b ) <= k, то если поделить строки a и b на подстроки методом rcut используя фактор сегментации
r >= ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) <= 1.
Выделение подстрок из базовой строки методом rcut выполняется по следующим принципам:
Выбирается значение, названное фактором сегментации, которое удовлетворяет условию
r >= ⌊k/2⌋ + 1
Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.
Теперь тоже самое, только на примере:
Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.
Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1
Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.
И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.
Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).
Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.
Но как производить поиск по подстрокам?
Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).
В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:
Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2
Затем эти таблицы сигнатур сортируются.
На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.
Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.
Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).
Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.
А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.
Такие действия надо произвести для всех подстрок и для всех таблиц.
И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) <= k.
Авторы предлагают использовать фильтр Блума [7] для уменьшения количества двоичных поисков.
Фильтр Блума может быстро определить находится ли подстрока в таблице с небольшим процентом ложных срабатываний. Что работает быстрее, чем хеш таблицы.
Если перед двоичным поиском подстроки в таблице фильтр возвращает, что эта подстрока не находится в этой таблице, то нет смысла производить поиск.
Соответственно надо создать по одному фильтру на каждую таблицу сигнатур.
Авторы также отмечают, что использование фильтра Блума таким способом снижает время обработки запросов в среднем на 57.8%.
Имеется база данных бинарных строк длиной 8 бит:
11111111
10000001
00111110
Задача найти все строки, где количество отличающихся битов не превышает 2 к целевой строке 10111111.
Значит требуемое расстояние k = 2.
1. Выбираем фактор сегментации.
Исходя из формулы, выбираем фактор сегментации r = 2 и значит всего будет две подстроки из одной строки.
2. Создаем набор сигнатур.
Так как количество подстрок 2, то требуется создать только 2 таблицы:
Т1 и Т2
3. Сохраняем подстроки в соответствующих таблицах с сохранением ссылки на первоисточник.
Т1 Т2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111
Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111
На этом предварительная обработка закончена. И приступаем к поиску.
1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.
2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.
2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010
2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101
3. Двоичный поиск.
3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Найдено две подстроки.
3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.
1100
0100
1000
1110 == 1110 => 00111110
1101
Найдена одна подстрока.
4. Объедением результаты в один список:
00111110
11111111
5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию <= 2:
HD( 10111110, 00111110 ) = 1
HD( 10111110, 11111111 ) = 2
Обе строки удовлетворяют условию различия не больше двух элементов.
Хотя на данном этапе и производится линейный поиск, но ожидается, что список строк кандидатов будет совсем не велик.
При условиях, когда число кандидатов будет велико, то предлагается использовать рекурсивный вариант HEngine.
На рисунке №1 показан пример работы алгоритма поиска.
Для длины строки 64 и предел расстояния 4, фактор сегментации равен 3, соответственно только 3 подстроки на строку.
Где T1, T2 и Т3 — это таблицы сигнатур, содержащие только подстроки B1, B2, B3, длинной 21, 21 и 22 бита.
Запрашиваемая строка делится на подстроки. Далее для соответствующих подстрок генерируются диапазон сигнатур. Для первой и второй сигнатуры количество комбинаций будет 22. А последняя сигнатура дает 23 варианта. И вконце производится двоичный поиск.
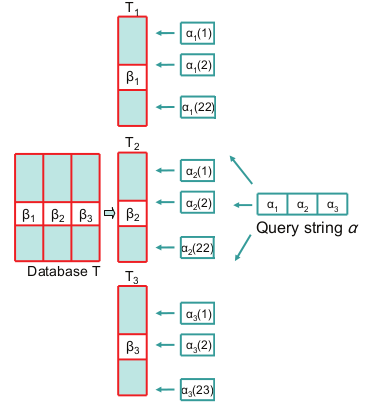
Рис 1. Упращенная версия обработки запросов к таблицам сигнатур.
Сложность подобного алгоритма в среднем случае O( P * ( log n + 1 ) ), где n — это общее число строк в базе данных, log n + 1 двоичный поиск, а P — количество двоичных поисков: считается, в нашем случае, как количество комбинаций на таблицу умнеженное на количество таблиц: P = ( 64 / r + 1 ) * r
В экстремальных случаях сложность может превышать линейную.
Отмечается, что такой подход использует в 4.65 меньше памяти и на 16 % быстрее, чем предыдущая работа описанная в [2]. И является самым быстрым способом из ныне известных, чтобы найти все строки в заданном пределе.
Все это конечно заманчиво, но пока не потрогаешь на деле, тяжело оценить масштабы.
Был создан прототип HEngine [9] и протестирован на имеющихся реальных данных.
Результаты обрадовали, т. к. поиск 343 хешей из базы в 752420 занимает ~0.1 секунды, что в 60 раз быстрее линейного поиска.
Казалось бы тут можно было остановиться. Но уж больно хотелось попробовать это использовать как-то в реальном проекте.
Имеется база данных хешей изображений, и бекенд на PHP.
Задача стояла как-то связать функциональность HEngine и PHP.
Решено было использовать FastCGI [10], в этом мне сильно помогли посты habrahabr.ru/post/154187 и habrahabr.ru/post/61532.
Из PHP достаточно вызвать:
Что за ~0.5 секунды возвращает результат. Когда линейным поиском требуется 9 секунд, а через запросы к MySQL не меньше 20 секунд.
Спасибо всем, кто осилил.
[1] M. Minsky and S. Papert. Perceptrons. MIT Press, Cambridge, MA, 1969.
[2] G. S. Manku, A. Jain, and A. D. Sarma. Detecting nearduplicates for web crawling. In Proc. 16Th WWW, May 2007.
[3] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: Nearest neighbor search in high-dimensional binary space. In MMSP, 2002.
[4] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: nearest neighbor search in high dimensional binary spaces. Journal of VLSI Signal Processing, Springer, 41(3):285–291, 2005.
[5] J. Landr ́e and F. Truchetet. Image retrieval with binary hamming distance. In Proc. 2nd VISAPP, 2007.
[6] H. Yang and Y. Wang. A LBP-based face recognition method with hamming distance constraint. In Proc. Fourth ICIG, 2007.
[7] B. Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of ACM, 13(7):422–426, 1970.
[8] Alex X. Liu, Ke Shen, Eric Torng. Large Scale Hamming Distance Query Processing. ICDE Conference, pages 553 — 564, 2011.
[9] github.com/valbok/HEngine Моя реализация HEngine на С++
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp Пример программы обвертки для поиска хешей через FastCGI.
Введение
Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.
Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.
Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.
Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.
Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.
Описание проблемы
Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.
Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.
В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.
— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.
В статье описывается решение только статической задачи.
Описание алгоритма HEngine для статической задачи
Данная реализация фокусируется на поиске строк в пределах k <= 10.
Существует три решения статической задачи: линейный поиск (linear scan), расширение запроса (query expansion) и расширение базы данных (table expansion).
В данном случае под расширением запроса имеется в виду генерация всех возможных вариантов строк, которые вписываются в заданное расстояние для первоначальной строки.
Расширение базы данных подразумевает создание множества копий этой базы данных, где или также генерируются все возможные варианты, которые отвечают требованиям необходимого расстояния, либо данные обрабатываются каким-то другим способом (подробно об этом чуть дальше.).
HEngine [8] использует комбинацию этих трех методов для эффективного балансирования между памятью и временем исполнения.
Немного теории
Алгоритм базируется на небольшой теореме, которая гласит следующее:
Если для двух строк a и b расстояние HD( a, b ) <= k, то если поделить строки a и b на подстроки методом rcut используя фактор сегментации
r >= ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) <= 1.
Выделение подстрок из базовой строки методом rcut выполняется по следующим принципам:
Выбирается значение, названное фактором сегментации, которое удовлетворяет условию
r >= ⌊k/2⌋ + 1
Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.
Теперь тоже самое, только на примере:
Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.
Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1
Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.
И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.
Предварительная обработка базы данных
Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).
Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.
Но как производить поиск по подстрокам?
Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).
В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:
Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2
Затем эти таблицы сигнатур сортируются.
Реализация поиска
На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.
Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.
Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).
Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.
А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.
Такие действия надо произвести для всех подстрок и для всех таблиц.
И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) <= k.
Фильтр Блума
Авторы предлагают использовать фильтр Блума [7] для уменьшения количества двоичных поисков.
Фильтр Блума может быстро определить находится ли подстрока в таблице с небольшим процентом ложных срабатываний. Что работает быстрее, чем хеш таблицы.
Если перед двоичным поиском подстроки в таблице фильтр возвращает, что эта подстрока не находится в этой таблице, то нет смысла производить поиск.
Соответственно надо создать по одному фильтру на каждую таблицу сигнатур.
Авторы также отмечают, что использование фильтра Блума таким способом снижает время обработки запросов в среднем на 57.8%.
Теперь тоже самое, только на примере
Имеется база данных бинарных строк длиной 8 бит:
11111111
10000001
00111110
Задача найти все строки, где количество отличающихся битов не превышает 2 к целевой строке 10111111.
Значит требуемое расстояние k = 2.
1. Выбираем фактор сегментации.
Исходя из формулы, выбираем фактор сегментации r = 2 и значит всего будет две подстроки из одной строки.
2. Создаем набор сигнатур.
Так как количество подстрок 2, то требуется создать только 2 таблицы:
Т1 и Т2
3. Сохраняем подстроки в соответствующих таблицах с сохранением ссылки на первоисточник.
Т1 Т2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111
Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111
На этом предварительная обработка закончена. И приступаем к поиску.
1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.
2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.
2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010
2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101
3. Двоичный поиск.
3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Найдено две подстроки.
3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.
1100
0100
1000
1110 == 1110 => 00111110
1101
Найдена одна подстрока.
4. Объедением результаты в один список:
00111110
11111111
5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию <= 2:
HD( 10111110, 00111110 ) = 1
HD( 10111110, 11111111 ) = 2
Обе строки удовлетворяют условию различия не больше двух элементов.
Хотя на данном этапе и производится линейный поиск, но ожидается, что список строк кандидатов будет совсем не велик.
При условиях, когда число кандидатов будет велико, то предлагается использовать рекурсивный вариант HEngine.
Наглядно
На рисунке №1 показан пример работы алгоритма поиска.
Для длины строки 64 и предел расстояния 4, фактор сегментации равен 3, соответственно только 3 подстроки на строку.
Где T1, T2 и Т3 — это таблицы сигнатур, содержащие только подстроки B1, B2, B3, длинной 21, 21 и 22 бита.
Запрашиваемая строка делится на подстроки. Далее для соответствующих подстрок генерируются диапазон сигнатур. Для первой и второй сигнатуры количество комбинаций будет 22. А последняя сигнатура дает 23 варианта. И вконце производится двоичный поиск.

Рис 1. Упращенная версия обработки запросов к таблицам сигнатур.
Результаты
Сложность подобного алгоритма в среднем случае O( P * ( log n + 1 ) ), где n — это общее число строк в базе данных, log n + 1 двоичный поиск, а P — количество двоичных поисков: считается, в нашем случае, как количество комбинаций на таблицу умнеженное на количество таблиц: P = ( 64 / r + 1 ) * r
В экстремальных случаях сложность может превышать линейную.
Отмечается, что такой подход использует в 4.65 меньше памяти и на 16 % быстрее, чем предыдущая работа описанная в [2]. И является самым быстрым способом из ныне известных, чтобы найти все строки в заданном пределе.
Реализация
Все это конечно заманчиво, но пока не потрогаешь на деле, тяжело оценить масштабы.
Был создан прототип HEngine [9] и протестирован на имеющихся реальных данных.
tests$ ./matches 7 data/db/table.txt data/query/face2.txt
Reading the dataset ........ done. 752420 db hashes and 343 query hashes.
Building with 7 hamming distance bound ....... done.
Building time: 12.964 seconds
Searching HEngine matches .......
found 100 total matches. HEngine query time: 0.1 seconds
Searching linear matches .......
found 100 total matches. Linear query time: 6.828 seconds
Результаты обрадовали, т. к. поиск 343 хешей из базы в 752420 занимает ~0.1 секунды, что в 60 раз быстрее линейного поиска.
Казалось бы тут можно было остановиться. Но уж больно хотелось попробовать это использовать как-то в реальном проекте.
В один клик до реального применения
Имеется база данных хешей изображений, и бекенд на PHP.
Задача стояла как-то связать функциональность HEngine и PHP.
Решено было использовать FastCGI [10], в этом мне сильно помогли посты habrahabr.ru/post/154187 и habrahabr.ru/post/61532.
Из PHP достаточно вызвать:
$list = file_get_contents( 'http://fcgi.local/?' . $hashes );
Что за ~0.5 секунды возвращает результат. Когда линейным поиском требуется 9 секунд, а через запросы к MySQL не меньше 20 секунд.
Спасибо всем, кто осилил.
Ссылки
[1] M. Minsky and S. Papert. Perceptrons. MIT Press, Cambridge, MA, 1969.
[2] G. S. Manku, A. Jain, and A. D. Sarma. Detecting nearduplicates for web crawling. In Proc. 16Th WWW, May 2007.
[3] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: Nearest neighbor search in high-dimensional binary space. In MMSP, 2002.
[4] M. L. Miller, M. A. Rodriguez, and I. J. Cox. Audio fingerprinting: nearest neighbor search in high dimensional binary spaces. Journal of VLSI Signal Processing, Springer, 41(3):285–291, 2005.
[5] J. Landr ́e and F. Truchetet. Image retrieval with binary hamming distance. In Proc. 2nd VISAPP, 2007.
[6] H. Yang and Y. Wang. A LBP-based face recognition method with hamming distance constraint. In Proc. Fourth ICIG, 2007.
[7] B. Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of ACM, 13(7):422–426, 1970.
[8] Alex X. Liu, Ke Shen, Eric Torng. Large Scale Hamming Distance Query Processing. ICDE Conference, pages 553 — 564, 2011.
[9] github.com/valbok/HEngine Моя реализация HEngine на С++
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp Пример программы обвертки для поиска хешей через FastCGI.
