<img src=«http:// » alt=«image»/>
» alt=«image»/>
Считаю уместным представить доказательство БТФ для третьей степени.
Во-первых: по данной методике любая степень может рассматриваться аналогично.
Во-вторых: до сих пор не существует доказательства для куба, основанного на элементарной математике.
И кроме того, за счёт небольших числовых значений при рассмотрении куба упрощаются расчёты, что облегчает понимание.
Благодарю заранее возможных оппонентов за полезные замечания по оформлению доказательства и, конечно, за помощь.
И немного желчи. В восприятии доказательства на Математическом форуме dxdy МГУ нет признаков понимания по существу.
При этом, необходимо заметить, что там сосредоточена часть математической общественности, занимающаяся проблемой БТФ значительное время, и даже профессионально. Именно на форуме dxdy потребовали, чтобы доказательство основывалось на рассмотрении куба. Такое требование считаю полезным, хотя взаимопониманию оно не помогло. Спрашивал:" Чего не хватает? Что ещё требуется рассмотреть?" Молчание, или, в лучшем случае, рекомендации доказать то, что уже давно доказано и, несомненно оппонентам известно. В настоящее время эта тема на форуме dxdy прикрыта: её можно читать, но отсутствует обратная связь. Может быть, кто-то на Хабрхабре конкретизирует требования. Хочется услышать мнение.
Доказательство может считаться справедливым, если оно удовлетворяет условию:
Показатель степени n – простое число. [1]
Рассмотрим доказательство Большой теоремы Ферма для куба.
Необходимо доказать, что

при целочисленных
 невозможно.
невозможно.
1.1 По существующей традиции в доказательстве рассматривается разность степеней

на основании удобства подбора оснований:

и
 .
.
1.2 При этом, при рассмотрении любой степени различают два случая Большой теоремы Ферма (БТФ).
1.1 К первому случаю БТФ относятся разности точных степеней с произвольными основаниями, за исключением оснований, обеспечивающих 2 Случай БТФ.
1.3 Для первого случая имеет место:
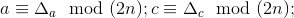

— взаимно простые числа, а основание
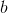 – чётное.
– чётное.
Именно, по этому варианту, требуется найти доказательство, и в первую очередь для второго случая БТФ.
1.4 Выразим основания равенства 1.1 для первого случая БТФ через единые аргументы, для чего вводим следующие обозначения:
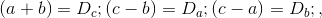
где, например,
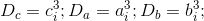
где
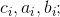 — целые числа. [2]
— целые числа. [2]
1.5 Поэтому равенство 1.1 может быть представлено в виде:
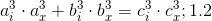
или
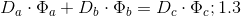
где:

2.1 И первый случай БТФ, и второй случаи БТФ доказываются на основании соизмеримости степеней и их оснований по
 .
.
Доказательство построено на сопоставлении величин:
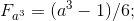 — со измеритель степени и
— со измеритель степени и
 — со измеритель основания.
— со измеритель основания.
2.2 При доказательстве первого случая БТФ при использовании
 и классов вычетов 1 и 5, можем выразить основания
и классов вычетов 1 и 5, можем выразить основания
 :
:
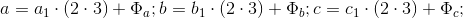
где:
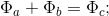
При этом
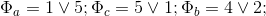
2.3 При рассмотрении первого случая БТФ, когда
 , основание
, основание
 может принадлежать к первому или пятому классам вычетов, а основание
может принадлежать к первому или пятому классам вычетов, а основание
 — наоборот.
— наоборот.
Потому что, основания, принадлежащие к чётным классам вычетов, не подходят, как и основания, принадлежащие к 3-у классу вычетов, так как в этом случае во всех основаниях возникают общие множители, что противоречит условиям теоремы.
2.4 При рассмотрении оснований степеней, принадлежащих к конкретному классу вычетов, корректировка величин оснований в уравнении Ферма зависит только от

Особенности первого и второго случаев БТФ влияют на расчётную закономерность, но принципиального значения для предлагаемого доказательства не представляют.
3.1 При рассмотрении доказательства для второго случая БТФ, выбор класса вычетов для оснований

и

значения не имеет, так как всегда можно использовать перевод любого из оснований к первому классу вычетов, используя для этого сомножитель, равный точной степени, на основании возможности перевода любого класса вычетов, взаимно простого с показателем рассматриваемой степени. (Малая теорема Ферма).
Поэтому, при рассмотрении второго случая БТФ достаточно рассмотрение варианта, когда

3.2 Для второго случая БТФ, который рассматривается более детально:
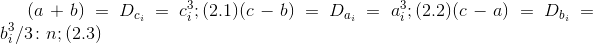
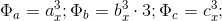
и
 , где
, где

— положительное число натурального числового ряда, взаимно простое с величиной.
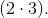
4.1 Существующая закономерность:
Величина
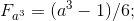
для точных кубов обязательно содержит сомножители

и сомножитель
 .
.
Поэтому, получаем возможность рассматривать и величину
 .
.
4.2 На основании найденных закономерностей, переходим к анализу разности степеней с целью ответа на вопрос:
Когда величина
 может содержать сомножитель
может содержать сомножитель
 ?
?
4.3 Для ответа на поставленный вопрос обратимся к рассмотрению разности степеней, приведенной к величине

на основании представления оснований

и

через

и
 и использования Бинома Ньютона. [3]
и использования Бинома Ньютона. [3]
5.1 Возможность приведения разности степеней к величине
 обеспечивается посредством использования
обеспечивается посредством использования
 .
.

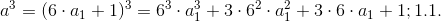 .
.
5.2 Определяем разность (1.1.с-1.1.а):
![(c^3-a^3)=6^3\cdot[(c_1)^3-(a_1)^3]+3\cdot 6^2\cdot[(c_1)^2-(a_1)^2]+3\cdot 6\cdot [(c_1)-(a_1)]; 1.1](https://habrastorage.org/getpro/habr/post_images/2e9/e39/28a/2e9e3928a25f05e2b3c7ed9e0276fca6.gif) .
.
5.3 Определяем
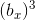 .
.
![(c^3-a^3)/[3\cdot 6\cdot (c_1-a_1)]=6\cdot 2\cdot[(c_1)^2+c_1\cdot(a_1)+(a_1)^2]+ 6\cdot [(c_1)+(a_1)]+1=b_x^3; 1.1.к](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
5.4 Определяем

![F_{b_{x}^{3}}=(b_{x}^{3}-1)/6=2\cdot[(c_{1})^{2}+c_{1}\cdot a_{1}+ a_{1})^{2}]+[(c_{1})+(a_{1})]; 1.1.к.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
Получаем сумму из двух слагаемых, первое из которых содержит сомножитель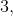 а второе нет.
а второе нет.
5.5 Это при условии, если сумма
![[(c_1)+(a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) сомножителей
сомножителей 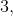 не содержит, а разность
не содержит, а разность

содержит, хотя бы, единичный сомножитель
 .
.
В этом случае и величина
 , содержать сомножитель
, содержать сомножитель
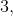 не может.
не может.
Для этого варианта всё ясно.
5.6 Для обеспечения точного куба в разности степеней отсутствие сомножителя

в величине

считаем условием не преодолимым для опровержения БТФ.
6.1 Для ответа на вопрос, почему и при наличии общих сомножителей
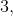 в величинах
в величинах
 и
и

невозможно получить в разности кубов точный куб, обратимся к формализованному выражению величины

6.2 Формализованное выражение
 ;
;
 O.1
O.1
Пример расчёта А:

 ;
;
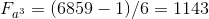 ;
;
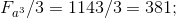
6.3 Определяем

через


6.4 В общем виде:
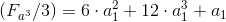 ; У.1
; У.1
6.5 Откуда точный куб:
 .
.
Эта закономерность освещена для возможности просчёта сомножителей

в величине
 .
.
7.1 Теперь зададимся вопросом, при каких значениях обеспечивается в величине

содержание сомножителей
 ,
,
в количестве, соответствующем наполнению аналогичной величины, при рассмотрении точного куба.
Пример:
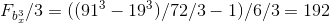 .
.
Так как

можно предположить, что основание предполагаемой степени
 ,
,
за вычетом единицы содержит два сомножителя
 .
.
7.2 А так как
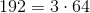 ,
,
при этом предположении

содержит единичный сомножитель
 ,
,
обеспечивается требуемое наполнение величины

сомножителями
 .
.
7.3 Попробуем ответить на вопрос, почему получается данный результат?
Подбором оснований степеней

и

Нами обеспечивалось выполнение условия:

и

содержат по одному общему сомножителю
 .
.
7.4 Мы этого добились.
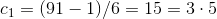
и

Но анализируя величину
 ,
,
замечаем, что обеспечили не единичный сомножитель
 ,
,
а

Такой результат получен потому, что сумма
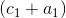
содержит не запланированный дополнительный сомножитель
 .
.
7.5 Этот сомножитель, по нашему мнению, можно считать неучтённым.
Если провести аналогию с бесконечно малыми, можно заметить, что, в отличии от не влияния бесконечно малых на конечный результат, неучтённый сомножитель обеспечивает тождество закономерностей, существующих в предполагаемых и истинных степенях, обеспечивая неопределённость, породившую рассматриваемую проблему.
По нашему мнению, обнаружение неучтённых сомножителей даёт объяснение причины возникновения затруднительности при поиске доказательства БТФ.
8.1 Кроме того можно заметить, что наличие неучтённого сомножителя при определении разности оснований степеней

и

исключает возможность получения точного куба в разности степеней, а возникновение неучтённого сомножителя в величине

является закономерностью, обеспечивающей предсказуемый результат.
8.2 И, по нашему мнению, это является препятствием, для опровержения утверждения БТФ, для второго случая при рассмотрении уравнения Ферма для третьей степени и при ответе на вопрос, почему и при наличии общих сомножителей
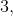
в величинах

и

опровержение БТФ невозможно.
8.3 Имеем право записать равенство:
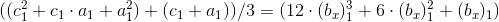 ,
,
или
 .
.
8.4 Что можно записать, как:
 . Т
. Т
8.5 Рассмотрим условие:
 .
.
Для этого условия
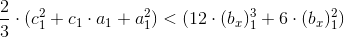
значительно, больше, чем на величину
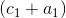 .
.
8.6 Это свидетельствует о том, что дальнейшее увеличение величины

смысла не имеет.
8.7 Чтобы показать невозможность опровержения БТФ и при меньших значениях
 ,
,
обратимся к рассмотрению возможности такого события, на примере рассмотрения закономерностей величин

и этих же величин, соответствующих получению точного куба, посредством умножения на
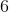
и прибавления
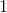 .
.
8.8 Для чего рассмотрим соотношение этих величин.
При
 ,
,
а

Параллельно рассматривается получение идентичного значения величины
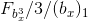
для оснований, имеющих

и
 ,
,
для подтверждения закономерности.
8.9 Если обозначить основание куба через
 ,
,
можно построить числовой ряд значений
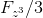 ,
,
для целочисленных величин
 :
:

и
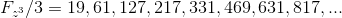 .
.
Получая расчётные значения
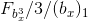 ,
,
получаем возможность сравнивать их с возможными значениями величин
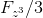 .
.
8.9.1
1. а
1.
 .
.
2.
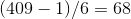 .
.
3.
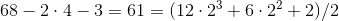 .
.
1.в
1.
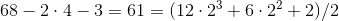 .
.
2.
 .
.
3.
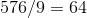 .
.
4.
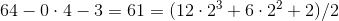 .
.
8.9.2
2. а
1
 .
.
2.
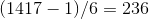
3.
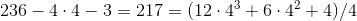
2.в
1.

2.
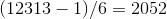
3.
 .
.
4.
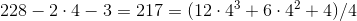 .
.
8.9.3
3. а
1
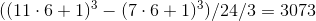 .
.
2.
 .
.
3.
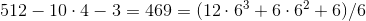 .
.
3.в
1.
 .
.
2
 .
.
3.
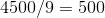 .
.
4.
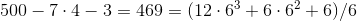 .
.
8.10
Рассмотрим расчёты сравниваемых величин для разности кубов, обеспечивающих предположение о возможности опровержения БТФ.
Диапазоне между основаниями равен
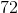 .
.
8.10.1 Для
 ,
,

получаем
 ,
,
где
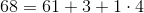
для
 ,
,
при
 .
.
Так как нас интересует разность оснований, когда
 ,
,
а
 ,
,
проводим аналогичный расчёт и при этих значениях.
 .
.
Сравниваем величины

и
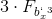 .
.
 .
.
Где:
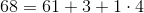 ,
,
для
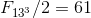 .
.
8.10.2 По аналогии, для

и

 .
.
Где
 ,
,
для
 .
.
8.10.3 По аналогии, для

и
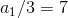
 .
.
Где
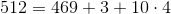 ,
,
для
 .
.
8.10.4 По аналогии, для
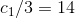
и

 .
.
Где
 ,
,
для
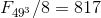 .
.
Получаем формализованную величину, влияющую на уменьшение разности сравниваемых нами величин, но частично, так как дополнительное приращение со знаком минус.
8.11 На основании числового ряда
 :
:
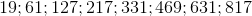 ,
,
установлено, что разность между соседними значениями всегда больше разности сравниваемых нами величин, как непосредственно, так и, соответственно, при их увеличении в три раза.
8.12 На основании расчётов видна следующая закономерность:
1. Минимальный диапазон между полученной величиной
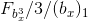
и, истинно возможным её значением

увеличивается на основании строгой закономерности, которая может быть формализована.
При этом он численно увеличивается, оставаясь минимальным, по сравнению с любым из числового ряда значений.
 ,
,
то есть, когда

и максимальным, когда

2. Поэтому, можно утверждать, что и величина

находится в такой же зависимости от истинно возможных таких величин.
Что даёт право утверждать, что опровержение БТФ для второго случая БТФ, для куба не возможно.
9.000 Когда то, на форуме dxdy кто то, по моему, с логином Brukvalub, мне написал:
«Вы так хотите разделаться с Большой теоремой Ферма?»
А почему не разделаться именно так.
Подход не оставляет вопросы без ответа.
А что ещё надо?
Конечно, конечно, понятное изложение и признание.
Кто-то написал на Хабрахабр, что доказательство становится доказательством только после его признания.
Не становится, а считается.
А становится доказательством после того, когда не остаётся каверзных вопросов.
Мне такие вопросы, в настоящий момент, не известны.
Правда, при молчащих оппонентах.
При наличии собеседника, а лучше соавтора, можно рассмотреть что то, и дополнительно. И детально рассмотрено то, что следует далее.
И ещё: показать оказалось тяжелее, чем доказать.
9.1 Перейдём к рассмотрению особенностей первого случая БТФ для куба.
С этой целью рассмотрим ещё одну найденную закономерность.
При определении
 справедливо:
справедливо:
![F_{b_x^n}=(b_x^n-1)/(2n)=[(c^n-a^n)/[n(c-a)]-1]/(2n)$$= [[(c^n-1)/(2\cdot n)-(a^n-1)/(2\cdot n)]/[n\cdot(c_1-a_1)] -1]/(2\cdot 3) ; F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a} ;](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
9.2 А, именно.
![F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a}ж](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif) .
.
Необходимость корректировки

объясняется разностью количества величин
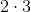 , принятых к расчёту.
, принятых к расчёту.
9.3 Это позволяет приравнять рассмотрение второго и первого случаев, так как нахождение разности степеней и для первого случая БТФ приводит к аналогичному варианту, тождественному второму случаю БТФ.
Поэтому можно заметить, что утверждение Большой теоремы Ферма справедливо, как для второго случая, так и для первого случаев при рассмотрении куба.
Что и требовалось доказать.
P.S. Доказательство для произвольной степени отличается от доказательства для куба особенностями расчёта и в числовом, и, конечно, в формализованном виде.
При этом, формализация величины
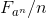
основана на аналогичных просчётам, используемых при рассмотрении куба.
Возникновение неучтённых сомножителей при рассмотрении БТФ при увеличении рассматриваемой степени имеет аналогичное объяснение с объяснением возникновения таких сомножителей при рассмотрении куба.
Кроме выше изложенного, следует заметить, что доказательство БТФ для произвольных показателей степеней просматривается и посредством использования наработок, найденных и при рассмотрении куба.
Конечно, всё не рассмотренное конкретно требует конкретного рассмотрения, но, в одиночестве, автору это не подъёмно.
К сожалению, и на Хабрахабре не обеспечивается желаемое.
Но, надежда, заключающаяся в том, что это, быть может, кому-то пригодиться.
Автор в истинности доказательства не сомневается, и удовлетворён этим.
И, особенно, тем, что доказательство стало возможно посредством использования закономерностей, так называемой элементарной математики, которые позволяют, не смотря на свою элементарность, добираться до сути, что не всегда удаётся её маститым собратьям.
Остаётся доказательство сократить и отполировать.
И здесь, не помешали бы советы.
Впрочем, если есть протестующие, или воздержавшиеся, милости просим к спичу.
Литература:
1. Г.Эдвардс «Последняя теорема Ферма».
2. М.М. Постников «Введение в теорию алгебраических чисел».
3. М.Я. Выгодский «Справочник по элементарной математике».
 » alt=«image»/>
» alt=«image»/>Считаю уместным представить доказательство БТФ для третьей степени.
Во-первых: по данной методике любая степень может рассматриваться аналогично.
Во-вторых: до сих пор не существует доказательства для куба, основанного на элементарной математике.
И кроме того, за счёт небольших числовых значений при рассмотрении куба упрощаются расчёты, что облегчает понимание.
Благодарю заранее возможных оппонентов за полезные замечания по оформлению доказательства и, конечно, за помощь.
И немного желчи. В восприятии доказательства на Математическом форуме dxdy МГУ нет признаков понимания по существу.
При этом, необходимо заметить, что там сосредоточена часть математической общественности, занимающаяся проблемой БТФ значительное время, и даже профессионально. Именно на форуме dxdy потребовали, чтобы доказательство основывалось на рассмотрении куба. Такое требование считаю полезным, хотя взаимопониманию оно не помогло. Спрашивал:" Чего не хватает? Что ещё требуется рассмотреть?" Молчание, или, в лучшем случае, рекомендации доказать то, что уже давно доказано и, несомненно оппонентам известно. В настоящее время эта тема на форуме dxdy прикрыта: её можно читать, но отсутствует обратная связь. Может быть, кто-то на Хабрхабре конкретизирует требования. Хочется услышать мнение.
Доказательство может считаться справедливым, если оно удовлетворяет условию:
Показатель степени n – простое число. [1]
Рассмотрим доказательство Большой теоремы Ферма для куба.
Необходимо доказать, что

при целочисленных
 невозможно.
невозможно.Вступление
1.1 По существующей традиции в доказательстве рассматривается разность степеней

на основании удобства подбора оснований:

и
 .
.1.2 При этом, при рассмотрении любой степени различают два случая Большой теоремы Ферма (БТФ).
1.1 К первому случаю БТФ относятся разности точных степеней с произвольными основаниями, за исключением оснований, обеспечивающих 2 Случай БТФ.
1.3 Для первого случая имеет место:
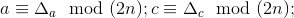

— взаимно простые числа, а основание
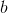 – чётное.
– чётное.Именно, по этому варианту, требуется найти доказательство, и в первую очередь для второго случая БТФ.
1.4 Выразим основания равенства 1.1 для первого случая БТФ через единые аргументы, для чего вводим следующие обозначения:
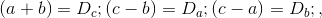
где, например,
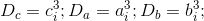
где
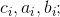 — целые числа. [2]
— целые числа. [2]1.5 Поэтому равенство 1.1 может быть представлено в виде:
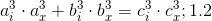
или
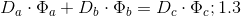
где:

2.1 И первый случай БТФ, и второй случаи БТФ доказываются на основании соизмеримости степеней и их оснований по
 .
.Доказательство построено на сопоставлении величин:
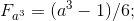 — со измеритель степени и
— со измеритель степени и — со измеритель основания.
— со измеритель основания.2.2 При доказательстве первого случая БТФ при использовании
 и классов вычетов 1 и 5, можем выразить основания
и классов вычетов 1 и 5, можем выразить основания  :
: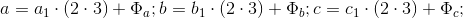
где:
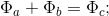
При этом
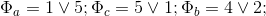
2.3 При рассмотрении первого случая БТФ, когда
 , основание
, основание  может принадлежать к первому или пятому классам вычетов, а основание
может принадлежать к первому или пятому классам вычетов, а основание  — наоборот.
— наоборот. Потому что, основания, принадлежащие к чётным классам вычетов, не подходят, как и основания, принадлежащие к 3-у классу вычетов, так как в этом случае во всех основаниях возникают общие множители, что противоречит условиям теоремы.
2.4 При рассмотрении оснований степеней, принадлежащих к конкретному классу вычетов, корректировка величин оснований в уравнении Ферма зависит только от

Особенности первого и второго случаев БТФ влияют на расчётную закономерность, но принципиального значения для предлагаемого доказательства не представляют.
3.1 При рассмотрении доказательства для второго случая БТФ, выбор класса вычетов для оснований

и

значения не имеет, так как всегда можно использовать перевод любого из оснований к первому классу вычетов, используя для этого сомножитель, равный точной степени, на основании возможности перевода любого класса вычетов, взаимно простого с показателем рассматриваемой степени. (Малая теорема Ферма).
Поэтому, при рассмотрении второго случая БТФ достаточно рассмотрение варианта, когда

3.2 Для второго случая БТФ, который рассматривается более детально:
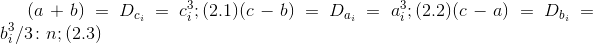
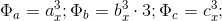
и
 , где
, где
— положительное число натурального числового ряда, взаимно простое с величиной.
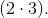
Доказательство второго случая БТФ.
4.1 Существующая закономерность:
Величина
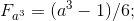
для точных кубов обязательно содержит сомножители

и сомножитель
 .
.Поэтому, получаем возможность рассматривать и величину
 .
. 4.2 На основании найденных закономерностей, переходим к анализу разности степеней с целью ответа на вопрос:
Когда величина
 может содержать сомножитель
может содержать сомножитель  ?
?4.3 Для ответа на поставленный вопрос обратимся к рассмотрению разности степеней, приведенной к величине

на основании представления оснований

и

через

и
 и использования Бинома Ньютона. [3]
и использования Бинома Ньютона. [3]5.1 Возможность приведения разности степеней к величине
 обеспечивается посредством использования
обеспечивается посредством использования  .
.
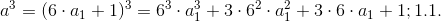 .
.5.2 Определяем разность (1.1.с-1.1.а):
![(c^3-a^3)=6^3\cdot[(c_1)^3-(a_1)^3]+3\cdot 6^2\cdot[(c_1)^2-(a_1)^2]+3\cdot 6\cdot [(c_1)-(a_1)]; 1.1](https://habrastorage.org/getpro/habr/post_images/2e9/e39/28a/2e9e3928a25f05e2b3c7ed9e0276fca6.gif) .
.5.3 Определяем
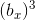 .
.![(c^3-a^3)/[3\cdot 6\cdot (c_1-a_1)]=6\cdot 2\cdot[(c_1)^2+c_1\cdot(a_1)+(a_1)^2]+ 6\cdot [(c_1)+(a_1)]+1=b_x^3; 1.1.к](https://habrastorage.org/getpro/habr/post_images/83f/241/a0a/83f241a0aa25fdfd5b3ff68b80033d6d.gif)
5.4 Определяем

![F_{b_{x}^{3}}=(b_{x}^{3}-1)/6=2\cdot[(c_{1})^{2}+c_{1}\cdot a_{1}+ a_{1})^{2}]+[(c_{1})+(a_{1})]; 1.1.к.1](https://habrastorage.org/getpro/habr/post_images/223/2ae/eff/2232aeeff09f111afbbbf7fcc022bc79.gif)
Получаем сумму из двух слагаемых, первое из которых содержит сомножитель
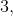 а второе нет.
а второе нет. 5.5 Это при условии, если сумма
![[(c_1)+(a_1)];](https://habrastorage.org/getpro/habr/post_images/e06/f46/80d/e06f4680d55a59544ff8cadd7de25e98.gif) сомножителей
сомножителей 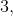 не содержит, а разность
не содержит, а разность
содержит, хотя бы, единичный сомножитель
 .
.В этом случае и величина
 , содержать сомножитель
, содержать сомножитель 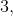 не может.
не может.Для этого варианта всё ясно.
5.6 Для обеспечения точного куба в разности степеней отсутствие сомножителя

в величине

считаем условием не преодолимым для опровержения БТФ.
6.1 Для ответа на вопрос, почему и при наличии общих сомножителей
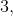 в величинах
в величинах  и
и 
невозможно получить в разности кубов точный куб, обратимся к формализованному выражению величины

6.2 Формализованное выражение
 ;
; O.1
O.1Пример расчёта А:

 ;
; 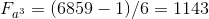 ;
;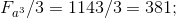
6.3 Определяем

через


6.4 В общем виде:
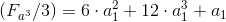 ; У.1
; У.16.5 Откуда точный куб:
 .
.Эта закономерность освещена для возможности просчёта сомножителей

в величине
 .
.7.1 Теперь зададимся вопросом, при каких значениях обеспечивается в величине

содержание сомножителей
 ,
,в количестве, соответствующем наполнению аналогичной величины, при рассмотрении точного куба.
Пример:
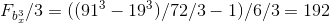 .
.Так как

можно предположить, что основание предполагаемой степени
 ,
,за вычетом единицы содержит два сомножителя
 .
.7.2 А так как
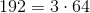 ,
,при этом предположении

содержит единичный сомножитель
 ,
,обеспечивается требуемое наполнение величины

сомножителями
 .
.7.3 Попробуем ответить на вопрос, почему получается данный результат?
Подбором оснований степеней

и

Нами обеспечивалось выполнение условия:

и

содержат по одному общему сомножителю
 .
.7.4 Мы этого добились.
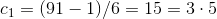
и

Но анализируя величину
 ,
,замечаем, что обеспечили не единичный сомножитель
 ,
,а

Такой результат получен потому, что сумма
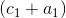
содержит не запланированный дополнительный сомножитель
 .
.7.5 Этот сомножитель, по нашему мнению, можно считать неучтённым.
Если провести аналогию с бесконечно малыми, можно заметить, что, в отличии от не влияния бесконечно малых на конечный результат, неучтённый сомножитель обеспечивает тождество закономерностей, существующих в предполагаемых и истинных степенях, обеспечивая неопределённость, породившую рассматриваемую проблему.
По нашему мнению, обнаружение неучтённых сомножителей даёт объяснение причины возникновения затруднительности при поиске доказательства БТФ.
8.1 Кроме того можно заметить, что наличие неучтённого сомножителя при определении разности оснований степеней

и

исключает возможность получения точного куба в разности степеней, а возникновение неучтённого сомножителя в величине

является закономерностью, обеспечивающей предсказуемый результат.
8.2 И, по нашему мнению, это является препятствием, для опровержения утверждения БТФ, для второго случая при рассмотрении уравнения Ферма для третьей степени и при ответе на вопрос, почему и при наличии общих сомножителей
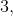
в величинах

и

опровержение БТФ невозможно.
8.3 Имеем право записать равенство:
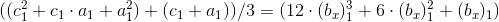 ,
,или
 .
.8.4 Что можно записать, как:
 . Т
. Т8.5 Рассмотрим условие:
 .
.Для этого условия
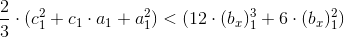
значительно, больше, чем на величину
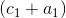 .
.8.6 Это свидетельствует о том, что дальнейшее увеличение величины

смысла не имеет.
8.7 Чтобы показать невозможность опровержения БТФ и при меньших значениях
 ,
, обратимся к рассмотрению возможности такого события, на примере рассмотрения закономерностей величин

и этих же величин, соответствующих получению точного куба, посредством умножения на
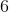
и прибавления
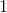 .
.8.8 Для чего рассмотрим соотношение этих величин.
При
 ,
,а

Параллельно рассматривается получение идентичного значения величины
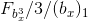
для оснований, имеющих

и
 ,
,для подтверждения закономерности.
8.9 Если обозначить основание куба через
 ,
,можно построить числовой ряд значений
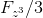 ,
,для целочисленных величин
 :
:
и
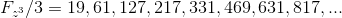 .
.Получая расчётные значения
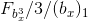 ,
,получаем возможность сравнивать их с возможными значениями величин
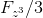 .
.8.9.1
1. а
1.
 .
.2.
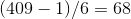 .
.3.
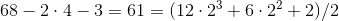 .
.1.в
1.
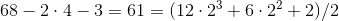 .
.2.
 .
.3.
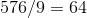 .
.4.
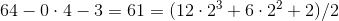 .
.8.9.2
2. а
1
 .
.2.
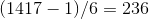
3.
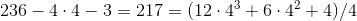
2.в
1.

2.
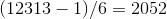
3.
 .
.4.
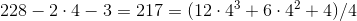 .
.8.9.3
3. а
1
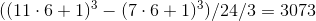 .
.2.
 .
.3.
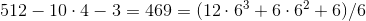 .
.3.в
1.
 .
.2
 .
.3.
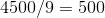 .
.4.
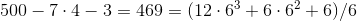 .
.8.10
Рассмотрим расчёты сравниваемых величин для разности кубов, обеспечивающих предположение о возможности опровержения БТФ.
Диапазоне между основаниями равен
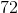 .
.8.10.1 Для
 ,
,
получаем
 ,
,где
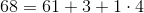
для
 ,
,при
 .
.Так как нас интересует разность оснований, когда
 ,
, а
 ,
,проводим аналогичный расчёт и при этих значениях.
 .
.Сравниваем величины

и
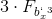 .
. .
.Где:
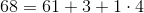 ,
,для
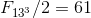 .
.8.10.2 По аналогии, для

и

 .
.Где
 ,
,для
 .
.8.10.3 По аналогии, для

и
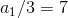
 .
.Где
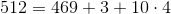 ,
,для
 .
.8.10.4 По аналогии, для
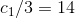
и

 .
.Где
 ,
,для
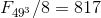 .
.Получаем формализованную величину, влияющую на уменьшение разности сравниваемых нами величин, но частично, так как дополнительное приращение со знаком минус.
8.11 На основании числового ряда
 :
: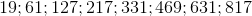 ,
, установлено, что разность между соседними значениями всегда больше разности сравниваемых нами величин, как непосредственно, так и, соответственно, при их увеличении в три раза.
8.12 На основании расчётов видна следующая закономерность:
1. Минимальный диапазон между полученной величиной
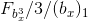
и, истинно возможным её значением

увеличивается на основании строгой закономерности, которая может быть формализована.
При этом он численно увеличивается, оставаясь минимальным, по сравнению с любым из числового ряда значений.
 ,
, то есть, когда

и максимальным, когда

2. Поэтому, можно утверждать, что и величина

находится в такой же зависимости от истинно возможных таких величин.
Что даёт право утверждать, что опровержение БТФ для второго случая БТФ, для куба не возможно.
9.000 Когда то, на форуме dxdy кто то, по моему, с логином Brukvalub, мне написал:
«Вы так хотите разделаться с Большой теоремой Ферма?»
А почему не разделаться именно так.
Подход не оставляет вопросы без ответа.
А что ещё надо?
Конечно, конечно, понятное изложение и признание.
Кто-то написал на Хабрахабр, что доказательство становится доказательством только после его признания.
Не становится, а считается.
А становится доказательством после того, когда не остаётся каверзных вопросов.
Мне такие вопросы, в настоящий момент, не известны.
Правда, при молчащих оппонентах.
При наличии собеседника, а лучше соавтора, можно рассмотреть что то, и дополнительно. И детально рассмотрено то, что следует далее.
И ещё: показать оказалось тяжелее, чем доказать.
9.1 Перейдём к рассмотрению особенностей первого случая БТФ для куба.
С этой целью рассмотрим ещё одну найденную закономерность.
При определении
 справедливо:
справедливо:![F_{b_x^n}=(b_x^n-1)/(2n)=[(c^n-a^n)/[n(c-a)]-1]/(2n)$$= [[(c^n-1)/(2\cdot n)-(a^n-1)/(2\cdot n)]/[n\cdot(c_1-a_1)] -1]/(2\cdot 3) ; F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a} ;](https://habrastorage.org/getpro/habr/post_images/da0/826/0d1/da08260d182e2fd35ade19371cd46c0b.gif)
9.2 А, именно.
![F_{b_x^n}=(b_x^n-1)/(2n)=\frac{[(c^n-a^n)/(c-a)-1]}{2n}= \frac{[(c^n \pm \Delta_c)/(2n)-( a^n \pm \Delta_a)]/(2n)-(c_1-a_1) }{c-a}ж](https://habrastorage.org/getpro/habr/post_images/790/a27/cdb/790a27cdb8b9f53f6ff59166405de8f6.gif) .
.Необходимость корректировки

объясняется разностью количества величин
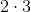 , принятых к расчёту.
, принятых к расчёту.9.3 Это позволяет приравнять рассмотрение второго и первого случаев, так как нахождение разности степеней и для первого случая БТФ приводит к аналогичному варианту, тождественному второму случаю БТФ.
Поэтому можно заметить, что утверждение Большой теоремы Ферма справедливо, как для второго случая, так и для первого случаев при рассмотрении куба.
Что и требовалось доказать.
P.S. Доказательство для произвольной степени отличается от доказательства для куба особенностями расчёта и в числовом, и, конечно, в формализованном виде.
При этом, формализация величины
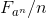
основана на аналогичных просчётам, используемых при рассмотрении куба.
Возникновение неучтённых сомножителей при рассмотрении БТФ при увеличении рассматриваемой степени имеет аналогичное объяснение с объяснением возникновения таких сомножителей при рассмотрении куба.
Кроме выше изложенного, следует заметить, что доказательство БТФ для произвольных показателей степеней просматривается и посредством использования наработок, найденных и при рассмотрении куба.
Конечно, всё не рассмотренное конкретно требует конкретного рассмотрения, но, в одиночестве, автору это не подъёмно.
К сожалению, и на Хабрахабре не обеспечивается желаемое.
Но, надежда, заключающаяся в том, что это, быть может, кому-то пригодиться.
Автор в истинности доказательства не сомневается, и удовлетворён этим.
И, особенно, тем, что доказательство стало возможно посредством использования закономерностей, так называемой элементарной математики, которые позволяют, не смотря на свою элементарность, добираться до сути, что не всегда удаётся её маститым собратьям.
Остаётся доказательство сократить и отполировать.
И здесь, не помешали бы советы.
Впрочем, если есть протестующие, или воздержавшиеся, милости просим к спичу.
Литература:
1. Г.Эдвардс «Последняя теорема Ферма».
2. М.М. Постников «Введение в теорию алгебраических чисел».
3. М.Я. Выгодский «Справочник по элементарной математике».