pchelintsev_an 10 мая 2018 в 22:48

Ищем циклы на аттракторе Лоренца в пакете Maxima

17 мин

4.9K

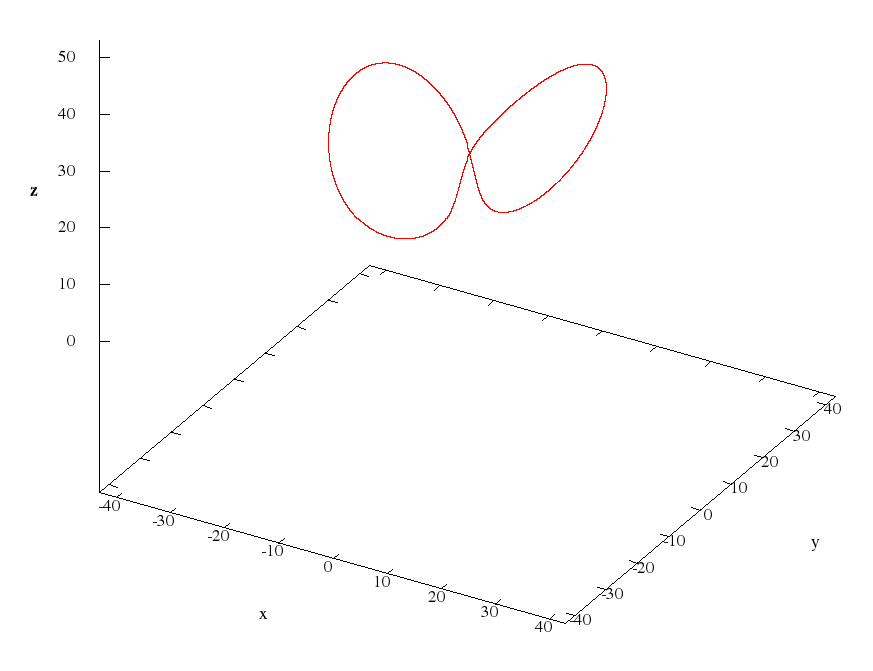
Этот топик продолжает серию моих статей на Хабре, посвященных исследованию аттрактора Лоренца.

Часть 1. Критический взгляд на аттрактор Лоренца
Часть 2. Динамическая система Лоренца и вычислительный эксперимент
Часть 3. О существовании периодических решений в системе Лоренца
Часть 4. Три цикла в аттракторе Лоренца

Итак, рассмотрим нелинейную систему дифференциальных уравнений, введенную Эдвардом Лоренцом в 1963 году:

$(1)\left\{ \begin{array}{l} \dot{x}=\sigma(y-x),\\ \dot{y}=rx-y-xz,\\ \dot{z}=xy-bz, \end{array}\right.$

где

$\sigma=10,\:r=28,\:b=8/3\:-$

классические значения параметров системы.

Для любого решения системы Лоренца есть такой момент времени, когда соответствующая фазовая траектория навсегда погружается в сферу фиксированного радиуса. Поэтому существует предельное множество — аттрактор Лоренца, — к которому притягиваются все траектории динамической системы, когда время стремится к бесконечности. Таким образом, аттрактор определяет поведение решений динамической системы на больших отрезках времени.

В 70-х гг. 20-ого века Гукенхеймер, Уильямс и Йорке на основе результатов численных экспериментов сформулировали гипотезу о структуре аттрактора Лоренца при классических значениях параметров системы, однако, соответствие этой гипотезы структуре притягивающего множества системы (1) не было строго доказано. В 2000 году Стивен Смейл составил список из 18 наиболее значительных математических проблем 21-ого века. Проблема структуры аттрактора Лоренца была включена в этот перечень под номером 14. Уорвик Такер в своей работе 2002 года доказал, строго говоря, гиперболичность аттрактора в системе (1), т.е. аттрактор состоит из траекторий, всюду плотных на нем, вдоль которых близкие траектории экспоненциально разбегаются (континуум седловых траекторий); это и создает их хаотическое поведение. Тогда (как отмечает Д.В. Аносов в послесловии к книге Ж. Палиса и В. ди Мелу «Геометрическая теория динамических систем», Мир, 1986, с. 285) в аттракторе системы (1) "может (а не редко и должно) существовать бесконечное число асимптотически устойчивых периодических траекторий", но, на мой взгляд, их область притяжения может быть достаточно малой (трудно улавливаемой в численном эксперименте). На основе вычислений в работе В.С. Афраймовича, В.В. Быкова и Л.П. Шильникова «О возникновении и структуре аттрактора Лоренца» (ДАН СССР, 1977. — Т. 234, №2, с. 336-339) описана структура аттрактора — в нем существует всюду плотное множество седловых циклов.

Как обычно отслеживают циклы в системе Лоренца? Используют символическую динамику — разбивают область в фазовом пространстве, содержащую аттрактор, на конечное число подобластей. Обозначая каждый элемент разбиения буквой, траектории на аттракторе, проходящие через соответствующие области, кодируются последовательностями таких символов. Если в последовательности имеется регулярность — повторяемость групп символов, — то мы имеем дело с циклом. Однако возращаемость траектории в некоторую окрестность своей части не говорит о ее замкнутости (часть 1). Вообще, критику результатов подобных вычислительных экспериментов можно найти в научной литературе (см., например, главу 4 «Can we trust in numerical computations of chaotic solutions of dynamical systems?», написанную французским математиком Рене Лози и опубликованную в 2013 году в книге «Topology and Dynamics of Chaos»).

В 2004 году Дивакар Вишванат опубликовал работу «The fractal property of the Lorenz attractor» (Physica D: Nonlinear Phenomena, 2004. — Vol. 190, iss. 1-2, с. 115-128), в которой привел начальные условия и периоды для трех циклов в аттракторе Лоренца. На мой взгляд, эта работа стала революционной в хаотической динамике, поскольку автор впервые показал конкретные значения фазовых координат и периода с достаточно большой точностью. Алгоритм вычислений был основан на методе Линдштедта-Пуанкаре (ЛП), на который (в отличие от методов численного интегрирования) не влияет устойчивость цикла, к которому строятся приближения.

Особенно впечатляет третий цикл.

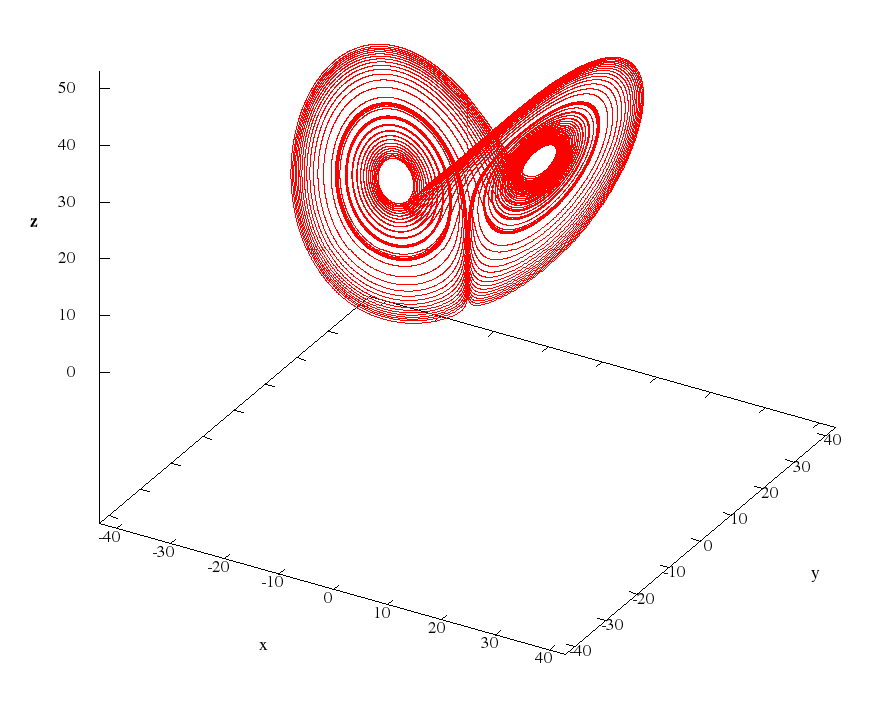
Может сложится впечатление, что здесь несколько циклов, но нет — данный цикл имеет такую многоспиральную структуру из-за доминирования большого числа (порядка 100) гармоник.

Анализ работ Вишваната показал, что автор приводит описание алгоритма без программной реализации (на MATLAB, как написано в его статьях). При этом не ясно, как для ЛП-метода символьно решается получаемая неоднородная линейная система дифференциальных уравнений с периодическими коэффициентами (например, для уравнения Ван дер Поля это сделать можно без особых проблем). На письма с просьбой прислать исходные тексты программ автор не отвечает. Можно понять — он привел данные, которые можно проверить (часть 4), решая задачу Коши высокоточными численными методами (часть 2), а как конкретно все сделано — тут уже алгоритм закрыт, оставляя за собой право единственного авторства. Поиск работ по цитированиям показал, что потом никто не воспроизвел алгоритм Вишваната для отыскания периодических решений в системе Лоренца.

Поэтому возникла идея открытого проекта, где каждый может скачать исходные тексты программы и найти новые циклы в системе Лоренца. В этом топике я опишу алгоритм работы программ, который, кстати, требует дальнейшей доработки по скорости, но один цикл уже получен. Интересно же найти среди хаоса порядок. ;)

Метод рядов Фурье

Поскольку еще имеются неясности с ЛП-методом, с подачи sliper01 было решено попробовать метод рядов Фурье для нелинейной системы (1). Для этого сделаем приближение фазовых координат на периоде тригонометрическими полиномами в общем виде с неизвестной циклической частотой (поскольку мы не знаем значение периода искомого периодического решения; в общем случае он может быть иррациональным числом):

$\begin{array}{l} \displaystyle x(t)\approx\tilde{x}_1(t)=x_{10}+\sum_{i=1}^h c_{1,i}\cos(i\omega t)+s_{1,i}\sin(i\omega t),\\ \displaystyle y(t)\approx\tilde{x}_2(t)=x_{20}+\sum_{i=1}^h c_{2,i}\cos(i\omega t)+s_{2,i}\sin(i\omega t),\\ \displaystyle z(t)\approx\tilde{x}_3(t)=x_{30}+\sum_{i=1}^h c_{3,i}\cos(i\omega t)+s_{3,i}\sin(i\omega t), \end{array}$

где h — заданное количество гармоник.

В силу правой части системы (1) составим невязки

$\begin{array}{l} \delta_1(t)=\tilde{x}'_1(t)-\sigma[\tilde{x}_2(t)-\tilde{x}_1(t)],\\ \delta_2(t)=\tilde{x}'_2(t)-[r\tilde{x}_1(t)-\tilde{x}_2(t)-\tilde{x}_1(t)\tilde{x}_3(t)],\\ \delta_3(t)=\tilde{x}'_3(t)-[\tilde{x}_1(t)\tilde{x}_2(t)-b\tilde{x}_3(t)], \end{array}$

где штрихом переобозначена производная функции по времени. Если производить вычисления в аналитическом виде на бумаге для малого числа гармоник (2-3), то для каждой невязки нужно следующее:

Продифференцировать по времени соответствующий тригонометрический полином;
Где имеются произведения фазовых координат, перемножить их, преобразовав произведения тригонометрических функций в суммы;
Привести подобные слагаемые для каждой функции cos() и sin() с соответствующим аргументом;
Поскольку мы работаем с количеством гармоник, равным h, отсечь от полученной невязки гармоники более высокого порядка;
Приравнять полученную невязку к нулю, т.е. коэффициенты при ее гармониках.

Если собрать в единое целое найденные алгебраические уравнения для каждой невязки, то получим пока еще незамкнутую систему нелинейных уравнений относительно неизвестных амплитуд, постоянных членов и циклической частоты. Количество неизвестных в системе равно

$display$

а уравнений — на единицу меньше.

Дополнительное уравнение можно взять из следующих соображений. В указанной выше литературе (и не только) отслеживают пересечения траекторий на аттракторе с плоскостью (или подобластями, через которые она проходит), где лежат положения равновесия системы

$O_1\left(-\sqrt{b(r-1)},\,-\sqrt{b(r-1)},\,r-1\right),\:\:O_2\left(\sqrt{b(r-1)},\,\sqrt{b(r-1)},\,r-1\right),$

параллельной плоскости xOy (сечение Пуанкаре). Таким образом, третья координата в начальном условии для искомых циклов равна величине r-1, откуда

$\tilde{x}_3(0)=r-1,$

тогда дополнительное уравнение системы имеет вид:

$x_{30}+\sum_{i=1}^h c_{3,i}-27=0.$

Других дополнительных сведений о периодических решениях в системе Лоренца я не встречал. Замечу, что для трех циклов, найденных Вишванатом, в начальном условии третьей координаты было взято число 27.

Далее приведен пример системы уравнений при h = 2:

$\left\{ \begin{array}{l} \omega s_{1,1}-10c_{2,1}+10c_{1,1}=0,\\ -10s_{2,1}+10s_{1,1}-c_{1,1}\omega=0,\\ 2\omega s_{1,2}-10c_{2,2}+10c_{1,2}=0,\\ -10s_{2,2}+10s_{1,2}-2c_{1,2}\omega=0,\\ 10x_{10}-10x_{20}=0,\\ c_{1,1}x_{30}+c_{3,1}x_{10}+\dfrac{s_{1,1}s_{3,2}}{2}+\dfrac{s_{1,2}s_{3,1}}{2}+\omega s_{2,1}+\dfrac{c_{1,1}c_{3,2}}{2}+\dfrac{c_{1,2}c_{3,1}}{2}+c_{2,1}-28c_{1,1}=0,\\ s_{1,1}x_{30}+s_{3,1}x_{10}+\dfrac{c_{1,1}s_{3,2}}{2}-\dfrac{c_{1,2}s_{3,1}}{2}+s_{2,1}+\dfrac{c_{3,1}s_{1,2}}{2}-\dfrac{c_{3,2}s_{1,1}}{2}-28s_{1,1}-c_{2,1}\omega=0,\\ c_{1,2}x_{30}+c_{3,2}x_{10}-\dfrac{s_{1,1}s_{3,1}}{2}+2\omega s_{2,2}+\dfrac{c_{1,1}c_{3,1}}{2}+c_{2,2}-28c_{1,2}=0,\\ s_{1,2}x_{30}+s_{3,2}x_{10}+\dfrac{c_{1,1}s_{3,1}}{2}+s_{2,2}-28s_{1,2}+\dfrac{c_{3,1}s_{1,1}}{2}-2c_{2,2}\omega=0,\\ x_{10}x_{30}+x_{20}-28x_{10}+\dfrac{s_{1,2}s_{3,2}}{2}+\dfrac{s_{1,1}s_{3,1}}{2}+\dfrac{c_{1,2}c_{3,2}}{2}+\dfrac{c_{1,1}c_{3,1}}{2}=0,\\ -c_{1,1}x_{20}-c_{2,1}x_{10}+\omega s_{3,1}-\dfrac{s_{1,1}s_{2,2}}{2}-\dfrac{s_{1,2}s_{2,1}}{2}+\dfrac{8c_{3,1}}{3}-\dfrac{c_{1,1}c_{2,2}}{2}-\dfrac{c_{1,2}c_{2,1}}{2}=0,\\ -s_{1,1}x_{20}-s_{2,1}x_{10}+\dfrac{8s_{3,1}}{3}-\dfrac{c_{1,1}s_{2,2}}{2}+\dfrac{c_{1,2}s_{2,1}}{2}-\dfrac{c_{2,1}s_{1,2}}{2}+\dfrac{c_{2,2}s_{1,1}}{2}-c_{3,1}\omega=0,\\ -c_{1,2}x_{20}-c_{2,2}x_{10}+2\omega s_{3,2}+\dfrac{s_{1,1}s_{2,1}}{2}+\dfrac{8c_{3,2}}{3}-\dfrac{c_{1,1}c_{2,1}}{2}=0,\\ -s_{1,2}x_{20}-s_{2,2}x_{10}+\dfrac{8s_{3,2}}{3}-\dfrac{c_{1,1}s_{2,1}}{2}-\dfrac{c_{2,1}s_{1,1}}{2}-2c_{3,2}\omega=0,\\ \dfrac{8x_{30}}{3}-x_{10}x_{20}-\dfrac{s_{1,2}s_{2,2}}{2}-\dfrac{s_{1,1}s_{2,1}}{2}-\dfrac{c_{1,2}c_{2,2}}{2}-\dfrac{c_{1,1}c_{2,1}}{2}=0,\\ x_{30}+c_{3,1}+c_{3,2}-27=0. \end{array}\right.$

Беглый анализ для трех и более гармоник показал, что найти формулы общего вида некоторых уравнений системы пока затруднительно. Отметим, что для любого h такая система имеет решения

$\begin{array}{c} \displaystyle x_{10}=x_{20}=\pm\sqrt{b(r-1)},\:x_{30}=r-1,\:c_{k,i}=0,\:s_{k,i}=0,\\ \omega\:-\:\mbox{любое число},\:\,k=\overline{1,3},\:i=\overline{1,h}, \end{array}$

соответствующие указанным положениям равновесия.

Пакет символьных вычислений Maxima

Итак, для получения приближения к периодическому решению мы должны получить нелинейную систему относительно неизвестных коэффициентов разложения и частоты. Как видно из приведенного примера, даже для двух гармоник система имеет громоздкий вид. Поэтому рассмотрим алгоритм проведения символьных вычислений для ее получения.

При разработке проекта мной был выбран математический пакет Maxima. Файл input_maxima.wxm с командами получения амплитуд и постоянных членов невязок при h = 2 представлен далее.

/* [wxMaxima batch file version 1] [ DO NOT EDIT BY HAND! ]*/

/* [wxMaxima: input start ] */

display2d:false$

x1:x10+c1c1*cos(1*omega*t)+s1c1*sin(1*omega*t)+

c1c2*cos(2*omega*t)+s1c2*sin(2*omega*t)$

x2:x20+c2c1*cos(1*omega*t)+s2c1*sin(1*omega*t)+

c2c2*cos(2*omega*t)+s2c2*sin(2*omega*t)$

x3:x30+c3c1*cos(1*omega*t)+s3c1*sin(1*omega*t)+

c3c2*cos(2*omega*t)+s3c2*sin(2*omega*t)$

assume(omega > 0)$

delta1:trigreduce(diff(x1,t)-(10*(x2-x1)),t)$

delta2:trigreduce(diff(x2,t)-(28*x1-x2-x1*x3),t)$

delta3:trigreduce(diff(x3,t)-(x1*x2-8/3*x3),t)$

expand(diff(delta1,cos(1*omega*t)));

expand(diff(delta1,sin(1*omega*t)));

expand(diff(delta1,cos(2*omega*t)));

expand(diff(delta1,sin(2*omega*t)));

expand(integrate(delta1,t,0,2*%pi/omega)*omega/(2*%pi));

expand(diff(delta2,cos(1*omega*t)));

expand(diff(delta2,sin(1*omega*t)));

expand(diff(delta2,cos(2*omega*t)));

expand(diff(delta2,sin(2*omega*t)));

expand(integrate(delta2,t,0,2*%pi/omega)*omega/(2*%pi));

expand(diff(delta3,cos(1*omega*t)));

expand(diff(delta3,sin(1*omega*t)));

expand(diff(delta3,cos(2*omega*t)));

expand(diff(delta3,sin(2*omega*t)));

expand(integrate(delta3,t,0,2*%pi/omega)*omega/(2*%pi));

/* [wxMaxima: input end ] */

Рассмотрим его подробнее. Комментарии в начале и конце нужны для того, чтобы файл можно было открыть в графическом фронтенде wxMaxima последних версий. Выражение display2d:false$ выключает многострочное рисование дробей, степеней и т.п. Знак $ позволяет вычислить результат выражения, но не выводить на экран (вместо ;). Функция trigreduce(выражение,t) свертывает все произведения тригонометрических функций относительно переменной t в комбинации сумм. Дифференцирование невязок по гармоническим функциям необходимо для получения соответствующих амплитуд. Функция expand(выражение) раскрывает скобки (выполняет умножение, возведение в степень, приводит подобные слагаемые). Для нахождения постоянных членов невязок применяется интегрирование на периоде, т.е. постоянный член k-ой невязки равен

$\dfrac{\displaystyle\omega\int_{0}^{\frac{2\pi}{\omega}}\delta_k(t)dt}{2\pi}.$

Чтобы при символьном интегрировании пакет не задавал вопрос о знаке частоты, дается команда

assume(omega > 0)$

Аналогично файл input_maxima.wxm формируется для любого количества гармоник. После выполнения данного скрипта пакет выведет в консоли символьные выражения для левой части системы алгебраических уравнений, которую я решал в нем же методом Ньютона. Например, для пяти гармоник скриптовый файл newton.wxm имеет следующий вид:

Скрипт newton.wxm для решения системы алгебраических уравнений методом Ньютона

/* [wxMaxima batch file version 1] [ DO NOT EDIT BY HAND! ]*/

/* [wxMaxima: input start ] */

display2d:false$

load(mnewton);

mnewton(

[

omega*s1c1-10*c2c1+10*c1c1,

-10*s2c1+10*s1c1-c1c1*omega,

2*omega*s1c2-10*c2c2+10*c1c2,

-10*s2c2+10*s1c2-2*c1c2*omega,

3*omega*s1c3-10*c2c3+10*c1c3,

-10*s2c3+10*s1c3-3*c1c3*omega,

4*omega*s1c4-10*c2c4+10*c1c4,

-10*s2c4+10*s1c4-4*c1c4*omega,

5*omega*s1c5-10*c2c5+10*c1c5,

-10*s2c5+10*s1c5-5*c1c5*omega,

10*x10-10*x20,



c1c1*x30+c3c1*x10+s1c4*s3c5/2+s1c5*s3c4/2+s1c3*s3c4/2+s1c4*s3c3/2+s1c2*s3c3/2+

s1c3*s3c2/2+s1c1*s3c2/2+s1c2*s3c1/2+omega*s2c1+c1c4*c3c5/2+c1c5*c3c4/2+

c1c3*c3c4/2+c1c4*c3c3/2+c1c2*c3c3/2+c1c3*c3c2/2+c1c1*c3c2/2+c1c2*c3c1/2+c2c1-

28*c1c1,



s1c1*x30+s3c1*x10+c1c4*s3c5/2-c1c5*s3c4/2+c1c3*s3c4/2-c1c4*s3c3/2+c1c2*s3c3/2-

c1c3*s3c2/2+c1c1*s3c2/2-c1c2*s3c1/2+s2c1+c3c4*s1c5/2-c3c5*s1c4/2+c3c3*s1c4/2-

c3c4*s1c3/2+c3c2*s1c3/2-c3c3*s1c2/2+c3c1*s1c2/2-c3c2*s1c1/2-28*s1c1-c2c1*omega,



c1c2*x30+c3c2*x10+s1c3*s3c5/2+s1c2*s3c4/2+s1c5*s3c3/2+s1c1*s3c3/2+s1c4*s3c2/2+

s1c3*s3c1/2-s1c1*s3c1/2+2*omega*s2c2+c1c3*c3c5/2+c1c2*c3c4/2+c1c5*c3c3/2+

c1c1*c3c3/2+c1c4*c3c2/2+c1c3*c3c1/2+c1c1*c3c1/2+c2c2-28*c1c2,



s1c2*x30+s3c2*x10+c1c3*s3c5/2+c1c2*s3c4/2-c1c5*s3c3/2+c1c1*s3c3/2-c1c4*s3c2/2-

c1c3*s3c1/2+c1c1*s3c1/2+s2c2+c3c3*s1c5/2+c3c2*s1c4/2-c3c5*s1c3/2+c3c1*s1c3/2-

c3c4*s1c2/2-28*s1c2-c3c3*s1c1/2+c3c1*s1c1/2-2*c2c2*omega,



c1c3*x30+c3c3*x10+s1c2*s3c5/2+s1c1*s3c4/2+s1c5*s3c2/2-s1c1*s3c2/2+s1c4*s3c1/2-

s1c2*s3c1/2+3*omega*s2c3+c1c2*c3c5/2+c1c1*c3c4/2+c1c5*c3c2/2+c1c1*c3c2/2+

c1c4*c3c1/2+c1c2*c3c1/2+c2c3-28*c1c3,



s1c3*x30+s3c3*x10+c1c2*s3c5/2+c1c1*s3c4/2-c1c5*s3c2/2+c1c1*s3c2/2-c1c4*s3c1/2+

c1c2*s3c1/2+s2c3+c3c2*s1c5/2+c3c1*s1c4/2-28*s1c3-c3c5*s1c2/2+c3c1*s1c2/2-

c3c4*s1c1/2+c3c2*s1c1/2-3*c2c3*omega,



c1c4*x30+c3c4*x10+s1c1*s3c5/2-s1c1*s3c3/2-s1c2*s3c2/2+s1c5*s3c1/2-s1c3*s3c1/2+

4*omega*s2c4+c1c1*c3c5/2+c1c1*c3c3/2+c1c2*c3c2/2+c1c5*c3c1/2+c1c3*c3c1/2+c2c4-

28*c1c4,



s1c4*x30+s3c4*x10+c1c1*s3c5/2+c1c1*s3c3/2+c1c2*s3c2/2-c1c5*s3c1/2+c1c3*s3c1/2+

s2c4+c3c1*s1c5/2-28*s1c4+c3c1*s1c3/2+c3c2*s1c2/2-c3c5*s1c1/2+c3c3*s1c1/2-

4*c2c4*omega,



c1c5*x30+c3c5*x10-s1c1*s3c4/2-s1c2*s3c3/2-s1c3*s3c2/2-s1c4*s3c1/2+5*omega*s2c5+

c1c1*c3c4/2+c1c2*c3c3/2+c1c3*c3c2/2+c1c4*c3c1/2+c2c5-28*c1c5,



s1c5*x30+s3c5*x10+c1c1*s3c4/2+c1c2*s3c3/2+c1c3*s3c2/2+c1c4*s3c1/2+s2c5-28*s1c5+

c3c1*s1c4/2+c3c2*s1c3/2+c3c3*s1c2/2+c3c4*s1c1/2-5*c2c5*omega,



x10*x30+x20-28*x10+s1c5*s3c5/2+s1c4*s3c4/2+s1c3*s3c3/2+s1c2*s3c2/2+s1c1*s3c1/2+

c1c5*c3c5/2+c1c4*c3c4/2+c1c3*c3c3/2+c1c2*c3c2/2+c1c1*c3c1/2,



-c1c1*x20-c2c1*x10+omega*s3c1-s1c4*s2c5/2-s1c5*s2c4/2-s1c3*s2c4/2-s1c4*s2c3/2-

s1c2*s2c3/2-s1c3*s2c2/2-s1c1*s2c2/2-s1c2*s2c1/2+8*c3c1/3-c1c4*c2c5/2-

c1c5*c2c4/2-c1c3*c2c4/2-c1c4*c2c3/2-c1c2*c2c3/2-c1c3*c2c2/2-c1c1*c2c2/2-

c1c2*c2c1/2,



-s1c1*x20-s2c1*x10+8*s3c1/3-c1c4*s2c5/2+c1c5*s2c4/2-c1c3*s2c4/2+c1c4*s2c3/2-

c1c2*s2c3/2+c1c3*s2c2/2-c1c1*s2c2/2+c1c2*s2c1/2-c2c4*s1c5/2+c2c5*s1c4/2-

c2c3*s1c4/2+c2c4*s1c3/2-c2c2*s1c3/2+c2c3*s1c2/2-c2c1*s1c2/2+c2c2*s1c1/2-

c3c1*omega,



-c1c2*x20-c2c2*x10+2*omega*s3c2-s1c3*s2c5/2-s1c2*s2c4/2-s1c5*s2c3/2-

s1c1*s2c3/2-s1c4*s2c2/2-s1c3*s2c1/2+s1c1*s2c1/2+8*c3c2/3-c1c3*c2c5/2-

c1c2*c2c4/2-c1c5*c2c3/2-c1c1*c2c3/2-c1c4*c2c2/2-c1c3*c2c1/2-c1c1*c2c1/2,



-s1c2*x20-s2c2*x10+8*s3c2/3-c1c3*s2c5/2-c1c2*s2c4/2+c1c5*s2c3/2-c1c1*s2c3/2+

c1c4*s2c2/2+c1c3*s2c1/2-c1c1*s2c1/2-c2c3*s1c5/2-c2c2*s1c4/2+c2c5*s1c3/2-

c2c1*s1c3/2+c2c4*s1c2/2+c2c3*s1c1/2-c2c1*s1c1/2-2*c3c2*omega,



-c1c3*x20-c2c3*x10+3*omega*s3c3-s1c2*s2c5/2-s1c1*s2c4/2-s1c5*s2c2/2+

s1c1*s2c2/2-s1c4*s2c1/2+s1c2*s2c1/2+8*c3c3/3-c1c2*c2c5/2-c1c1*c2c4/2-

c1c5*c2c2/2-c1c1*c2c2/2-c1c4*c2c1/2-c1c2*c2c1/2,



-s1c3*x20-s2c3*x10+8*s3c3/3-c1c2*s2c5/2-c1c1*s2c4/2+c1c5*s2c2/2-c1c1*s2c2/2+

c1c4*s2c1/2-c1c2*s2c1/2-c2c2*s1c5/2-c2c1*s1c4/2+c2c5*s1c2/2-c2c1*s1c2/2+

c2c4*s1c1/2-c2c2*s1c1/2-3*c3c3*omega,



-c1c4*x20-c2c4*x10+4*omega*s3c4-s1c1*s2c5/2+s1c1*s2c3/2+s1c2*s2c2/2-

s1c5*s2c1/2+s1c3*s2c1/2+8*c3c4/3-c1c1*c2c5/2-c1c1*c2c3/2-c1c2*c2c2/2-

c1c5*c2c1/2-c1c3*c2c1/2,



-s1c4*x20-s2c4*x10+8*s3c4/3-c1c1*s2c5/2-c1c1*s2c3/2-c1c2*s2c2/2+

c1c5*s2c1/2-c1c3*s2c1/2-c2c1*s1c5/2-c2c1*s1c3/2-c2c2*s1c2/2+c2c5*s1c1/2-

c2c3*s1c1/2-4*c3c4*omega,



-c1c5*x20-c2c5*x10+5*omega*s3c5+s1c1*s2c4/2+s1c2*s2c3/2+s1c3*s2c2/2+

s1c4*s2c1/2+8*c3c5/3-c1c1*c2c4/2-c1c2*c2c3/2-c1c3*c2c2/2-c1c4*c2c1/2,



-s1c5*x20-s2c5*x10+8*s3c5/3-c1c1*s2c4/2-c1c2*s2c3/2-c1c3*s2c2/2-c1c4*s2c1/2-

c2c1*s1c4/2-c2c2*s1c3/2-c2c3*s1c2/2-c2c4*s1c1/2-5*c3c5*omega,



8*x30/3-x10*x20-s1c5*s2c5/2-s1c4*s2c4/2-s1c3*s2c3/2-s1c2*s2c2/2-s1c1*s2c1/2-

c1c5*c2c5/2-c1c4*c2c4/2-c1c3*c2c3/2-c1c2*c2c2/2-c1c1*c2c1/2,



x30+c3c1+c3c2+c3c3+c3c4+c3c5-27

],

[

omega,x10,x20,x30,c1c1,s1c1,c1c2,s1c2,c1c3,s1c3,c1c4,s1c4,c1c5,s1c5,c2c1,s2c1,

c2c2,s2c2,c2c3,s2c3,c2c4,s2c4,c2c5,s2c5,c3c1,s3c1,c3c2,s3c2,c3c3,s3c3,c3c4,

s3c4,c3c5,s3c5

],

[

4,0,0,0,-1,0,-1,1,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,0,-1,

0,-1,0

]

);

/* [wxMaxima: input end ] */

Данный скрипт приведен по причине того, что среди многочисленных подборов начальных приближений для метода Ньютона было найдено такое, которое дает приближение к первому циклу Вишваната (первый рисунок в данном топике, часть 4). Результатом выполнения скрипта являются следующие значения:

(%o3) [[omega = 3.984915779315225,x10 = -1.0530814406427574E-19,

 x20 = -1.0530848010639959E-19,x30 = 23.17484126777741,

 c1c1 = -5.73442859974501,s1c1 = 8.700967706873968,

 c1c2 = -6.138073055934428E-19,s1c2 = -7.0677320406008846E-19,

 c1c3 = 3.162874335852723,s1c3 = 2.061936729442591,

 c1c4 = -8.5085912287645265E-19,s1c4 = 4.9192865298350146E-19,

 c1c5 = 0.52386925730497,s1c5 = -0.691987635106,

 c2c1 = -2.267166248701582,s2c1 = 10.98608920812201,

 c2c2 = -1.210031439700999E-18,s2c2 = -2.9446761267244605E-19,

 c2c3 = 5.627867598584345,s2c3 = -1.719199625236613,

 c2c4 = -1.5456862362288386E-19,s2c4 = 1.8698116859813374E-18,

 c2c5 = -0.8548869658075,s2c5 = -1.735775069972357,

 c3c1 = -3.7683970563654851E-19,s3c1 = 5.9125298542126567E-19,

 c3c2 = 7.278395231560698,s3c2 = -9.743072005078496,

 c3c3 = 1.1948226901634459E-18,s3c3 = 1.5220232872406872E-18,

 c3c4 = -3.45323649933811,s3c4 = -1.496599920543623,

 c3c5 = 9.6317779065317723E-19,s3c5 = -1.0610022378452297E-18]]

Период, соответствующий вычисленной частоте, равен 1.576742309033. Полученное начальное условие

x(0) = -2.047685006587,

y(0) = 2.505814384075,

z(0) = 27.

Для 20-ти гармоник результаты следующие:

Решение системы методом Ньютона для 20-ти гармоник

(%o8) [[omega = 4.031165684154375,x10 = 3.452436636135707E-50,

 x20 = 3.4523754614063194E-50,x30 = 23.04210398998602,

 c1c1 = -5.780477208090859,s1c1 = 8.560177260062323,

 c1c2 = 3.3849413337079056E-49,s1c2 = 1.5989214550115505E-49,

 c1c3 = 3.160763451378848,s1c3 = 2.239210971634309,

 c1c4 = -1.21170336257605E-49,s1c4 = -3.818560050552285E-49,

 c1c5 = 0.69588654260783,s1c5 = -0.79793931881183,

 c1c6 = -2.573166948839488E-49,s1c6 = 1.1784781435511185E-49,

 c1c7 = -0.18919938918705,s1c7 = -0.18649196579137,

 c1c8 = 4.726991731347519E-50,s1c8 = 1.3899389953829603E-49,

 c1c9 = -0.047704234826538,s1c9 = 0.045540484243309,

 c1c10 = 6.188407076631053E-50,s1c10 = -7.639867254285597E-51,

 c1c11 = 0.011123224835893,s1c11 = 0.012091350850322,

 c1c12 = 2.719675531744166E-51,s1c12 = -2.0174635578405016E-50,

 c1c13 = 0.0030611621974957,s1c13 = -0.0027350588873308,

 c1c14 = -4.328500181354198E-51,s1c14 = -1.8069147957343567E-51,

 c1c15 = -6.743818650154738E-4,s1c15 = -7.747451562726169E-4,

 c1c16 = 2.478940226869119E-52,s1c16 = 9.920503542095918E-52,

 c1c17 = -1.9589381003970067E-4,s1c17 = 1.6639570540310215E-4,

 c1c18 = 7.613414122410434E-52,s1c18 = -7.442026904972938E-52,

 c1c19 = 4.0812624026752806E-5,s1c19 = 4.925750678443421E-5,

 c1c20 = -4.3707528022580176E-52,s1c20 = -6.289684581250124E-52,

 c2c1 = -2.329727925986672,s2c1 = 10.89038339599156,

 c2c2 = 6.720316046845365E-49,s2c2 = 5.403930895172978E-51,

 c2c3 = 5.868752579909109,s2c3 = -1.583257376644017,

 c2c4 = -6.152200609127305E-49,s2c4 = -5.625603644581473E-49,

 c2c5 = -0.91242625740805,s2c5 = -2.2005562941246,

 c2c6 = -2.6425460251008945E-49,s2c6 = 6.265461950104472E-49,

 c2c7 = -0.71544539819512,s2c7 = 0.3473938938163,

 c2c8 = 4.034378786189927E-49,s2c8 = 1.3282395907330942E-49,

 c2c9 = 0.11751887876272,s2c9 = 0.21861379122273,

 c2c10 = 7.993269587641813E-50,s2c10 = -1.9937084927984E-49,

 c2c11 = 0.064739687321073,s2c11 = -0.037232167630822,

 c2c12 = -7.417411468340943E-50,s2c12 = -4.344654133333081E-50,

 c2c13 = -0.011271955992478,s2c13 = -0.018777126492758,

 c2c14 = -1.775229599542814E-50,s2c14 = 2.0696991298962414E-50,

 c2c15 = -0.0053590709969119,s2c15 = 0.0033030723921269,

 c2c16 = 7.2265249014967E-51,s2c16 = 4.381599209225772E-51,

 c2c17 = 9.444129079000977E-4,s2c17 = 0.0015088523935126,

 c2c18 = 3.308533281039877E-52,s2c18 = -5.396912369449293E-51,

 c2c19 = 4.1808644899593664E-4,s2c19 = -2.633351471837523E-4,

 c2c20 = -4.2043760181902243E-51,s2c20 = -1.8891776013678853E-52,

 c3c1 = 2.6457417929640968E-49,s3c1 = -2.9044228066628453E-49,

 c3c2 = 7.568407928271316,s3c2 = -9.50386771016789,

 c3c3 = -7.752066601960598E-49,s3c3 = -5.325333602855936E-50,

 c3c4 = -3.555328108662564,s3c4 = -1.844708804346798,

 c3c5 = 2.525273253202025E-49,s3c5 = 7.345202041266542E-49,

 c3c6 = -0.47412105737004,s3c6 = 1.279043509640932,

 c3c7 = 4.879750740269481E-49,s3c7 = -2.485410168207022E-49,

 c3c8 = 0.42272931170735,s3c8 = 0.12745697602359,

 c3c9 = -1.331077282513615E-49,s3c9 = -2.7599603145404137E-49,

 c3c10 = 0.034983961784989,s3c10 = -0.13153376199379,

 c3c11 = -1.3182244718693042E-49,s3c11 = 4.505225180687296E-50,

 c3c12 = -0.039340007400405,s3c12 = -0.0096456631299344,

 c3c13 = 5.58036901051472E-51,s3c13 = 4.939399058200867E-50,

 c3c14 = -0.0026598668892066,s3c14 = 0.011454996961114,

 c3c15 = 1.4821245205494333E-50,s3c15 = 1.088094520038754E-52,

 c3c16 = 0.0032705398994219,s3c16 = 7.332382134713727E-4,

 c3c17 = -2.527258067297002E-51,s3c17 = -4.8845083754423576E-51,

 c3c18 = 2.0071100728640047E-4,s3c18 = -9.171720748149994E-4,

 c3c19 = -3.031273476536678E-51,s3c19 = 3.249303398257501E-51,

 c3c20 = -2.4740233416222174E-4,s3c20 = -5.132249907623684E-5]]

Здесь точность представления вещественного числа — 30 значащих цифр после точки, команда пакета

(fpprec:30,newtonepsilon:bfloat(10^(-fpprec+5)))$

Тогда полученный период T = 1.558652211165 (совпало 8 знаков после точки со значением, указанным Вишванатом), начальное условие

x(0) = -2.147375914135,

y(0) = 2.078143036771,

z(0) = 27.

Проверку этих чисел нужно делать численным решением задачи Коши (на больших отрезках времени перейти к высокоточным вычислениям). Я использую метод степенных рядов для построения неустойчивых решений системы Лоренца, описанный в части 2. Точность по ряду взял равной 1E-14, 80 бит под мантиссу вещественного числа. Приведу значения фазовых координат, вычисленных через период:

x(T) = -2.147466991199,

y(T) = 2.078421751536,

z(T) = 27.000633876853.

Увеличение точности по ряду не дает значительного эффекта на полученные значения. Как видно, из-за неустойчивости искомого решения (особенно на больших отрезках времени) нужно брать достаточно большое количество гармоник.

В методе Ньютона основной проблемой является выбор начального приближения, а для нашей задачи при его подборе имеет место частая сходимость метода к решениям, соответствующим положениям равновесия. Если получается отрицательное значение частоты, то это симметричное решение — изменив ее знак, мы меняем знаки на противоположные у коэффициентов синусов.

Автоматизация вычислений

Поскольку мы имеем дело с громоздкой системой уравнений, нужны программы, которые будут формировать скрипты для Maxima, запускать пакет и читать результаты вычислений. Такие программы были написаны на языке C++. Все исходные тексты, а также скрипты для пакета, собраны в проект periodic_sols на GitHub. Разберем их.

Взаимодействие с пакетом будем вести через перенаправление ввода/вывода на файлы. Пример команды запуска пакета:

maxima < input_maxima.wxm > output_maxima.txt

Для чтения из текстового файла результатов выполнения команд имеется функция ReadFromMaxima() (файлы maxima.h и maxima.cpp).

void ReadFromMaxima(std::fstream &f, std::string &res)
{
    std::string s;
    res = "";
    while(1)
    {
        f >> s;
        if(s[1] == '%' && s[2] == 'o')
        {
            while(1)
            {
                f >> s;
                if(s[1] == '%' && s[2] == 'i')
                    break;
                res += s;
            }
            break;
        }
    }
}

Первый аргумент — поток, связанный, например, с файлом output_maxima.txt, второй — строка, в которую считается результат. Если он многострочный (Maxima разбивает длинные строки на части), то результирующие строки склеятся в одну строку. Для запуска пакета применяется стандартная библиотечная функция system() из cstdlib.

Проект periodic_sols состоит из трех программ: periodic_sols.cpp, init_newton.cpp и calc_init_point.cpp. Для их сборки запускаем

./compile

Перед запуском ./periodic_sols необходимо подготовить файлы input.txt и system.txt. Формат первого файла (я не стал заморачиваться с интерфейсом — все программы консольные):

1-ая строка — порядок системы (в нашем случае он равен 3, в программе хранится в переменной n, это сделано не только для рассматриваемой системы);
2-ая строка — количество гармоник;
3-я строка — точность представления вещественного числа;
4-ая строка — номер фазовой координаты для дополнительного уравнения (в нашем случае он равен 3);
5-ая строка — значение этой координаты (в нашем случае оно равно 27);
6-ая строка — начальное приближение по частоте;
7-ая строка — начальное приближение по постоянным членам;
8-ая строка — начальное приближение по амплитудам косинусов (по синусам берется 0).

В файле system.txt находится правая часть динамической системы:

10*(x2-x1)

28*x1-x2-x1*x3

x1*x2-8/3*x3

В результате получается файл newton.wxm с командами для метода Ньютона. Этот файл подается на вход пакету. Программа init_newton.cpp создает файл new_newton.wxm на базе файла newton.wxm, записывая туда результаты вычислений для предыдущего количества гармоник (переменная prev_harmonics), меньшего или равного текущему числу (переменная harmonics). Это необходимо, когда мы хотим улучшить приближение к периодическому решению. Здесь алгоритм такой:

Решив систему нелинейных уравнений для малого количества гармоник (prev_harmonics), формируем файл res_newton.txt по результатам вычислений;
В файле input.txt увеличиваем количество гармоник и запускаем ./periodic_sols для формирования новой системы;
Запускаем программу ./init_newton, которая переносит вычисленные значения на соответствующие места начального приближения для новой системы, а недостающие заполняет нулями.

Пример файла res_newton.txt

6

(%o3) [[omega = 4.015535723138496,x10 = 1.1163935455233309E-34,

 x20 = 1.1163917124007318E-34,x30 = 23.11489854425051,

 c1c1 = -5.858151176772754,s1c1 = 8.558209161319546,

 c1c2 = 1.960681230817389E-33,s1c2 = -2.7310255660879398E-34,

 c1c3 = 3.087267195066005,s1c3 = 2.281499003542988,

 c1c4 = 8.751734521089439E-35,s1c4 = -1.3976296305135868E-33,

 c1c5 = 0.68554991009801,s1c5 = -0.71564273748697,

 c1c6 = -5.6780776064982454E-34,s1c6 = -7.460008287568864E-35,

 c2c1 = -2.421571715435777,s2c1 = 10.91057069350722,

 c2c2 = 1.748272524030671E-33,s2c2 = -1.8302254187761085E-33,

 c2c3 = 5.835699420375529,s2c3 = -1.437610509055349,

 c2c4 = -2.135841093020441E-33,s2c4 = -1.542027540239589E-33,

 c2c5 = -0.75129457859378,s2c5 = -2.092067814483454,

 c2c6 = -7.485715281433705E-34,s2c6 = 1.2824593776303231E-33,

 c3c1 = -1.1949726595573974E-33,s3c1 = -2.960055854830781E-33,

 c3c2 = 7.664015276863863,s3c2 = -9.413447797095198,

 c3c3 = -3.188941870009158E-33,s3c3 = 2.3150410742059717E-34,

 c3c4 = -3.401518244979598,s3c4 = -1.839151802556927,

 c3c5 = 4.259901987771216E-34,s3c5 = 2.1468791686456547E-33,

 c3c6 = -0.37739557613478,s3c6 = 1.074214498018439]]

Программа calc_init_point.cpp на базе файла res_newton.txt вычисляет начальные условия и период, записывая в файл init_point.txt. Буква «b» означает то же самое, что и буква «E» в представлении вещественного числа.

Что дальше?

Самая затратная по времени операция — символьное интегрирование. Например, для 120 гармоник время формирования системы — более 2-х суток. Тут можно распараллелить вычислительный процесс на три нода, но это значительного эффекта не даст (Вишванат, вообще, вычислял 1024 гармоники). Здесь нужно изменить принцип формирования постоянных членов. Например, вычесть из общего выражения полученные до этого выражения для каждой гармоники. Кстати, при решении системы нелинейных уравнений методом Ньютона матрица Якоби не обращается, в пакете используется LU-разложение для решения системы линейных уравнений на каждой итерации метода;
Сейчас я ищу аналогии в получаемых системах нелинейных уравнений для разных количеств гармоник, чтобы система формировалась сразу. Если кто-нибудь тоже хочет попробовать, то здесь имеется архив с системами для 2-7 гармоник. Если нужно еще, пишите в комментариях, добавлю;
В директорию T__undefined помещены приближения к пока еще неизвестному периодическому решению системы Лоренца (номерные директории внутри соответствуют найденному количеству гармоник). Пока еще недосчитал. Если метод для данного случая все-таки сходится, то период цикла будет больше периода третьего цикла Вишваната;
Как писал выше, главная проблема метода Ньютона — это выбор начального приближения. Если будет получен общий вид системы, то хорошо бы отделить от нее решения, соответствующие положениям равновесия, т.е. получить новую систему, решения которой — только искомые периодические решения. Тогда начальное приближение гораздо проще подбирать. Отмечу, конце исходного файла periodic_sols.cpp приведен комментарий с первоначально подобранными начальными приближениями для первого цикла Вишваната (как потом выяснилось) и неизвестного периодического решения.

Теги:

Хабы:

Ищем циклы на аттракторе Лоренца в пакете Maxima

Метод рядов Фурье

Пакет символьных вычислений Maxima

Автоматизация вычислений

Что дальше?

Публикации

Истории

Работа

Ближайшие события