Математика
В 2005 году ученые Джон Конуэй (John Conway) и Александр Сойфер (Alexander Soifer) решили написать «самую короткую научную статью по математике в мире». Непосредственно тело статьи состоит из двух слов (и двух иллюстраций — в них содержится ответ на вопрос, поставленный в заглавии).

Теория игр

За пятый параграф Джон Нэш получил Нобелевскую премию по экономике в 1994 году.
Кстати, в 2015 году Джон Нэш получил высшую награду по математике — Абелевскую премию за вклад в теорию нелинейных дифференциальных уравнений. Получив и Нобелевскую, и Абелевскую премии — Джон Форбс Нэш стал первым человеком в мире, который был удостоен обеих престижных наград.
Физика
Группа исследователей из Физической лаборатории в Бристоле и Индийского технологического института опубликовала в этот период времени статью:

«Можно ли объяснить сверхсветовую скорость нейтрино слабым квантовым измерением?»
Почти самое короткое «Abstract»: «Скорее всего, нет».
Сейсмология

Самое короткое «Abstract»
«Без химии»

«Исчерпывающий обзор потребительских продуктов, не содержащих «химии»
В 2016 году такая работа появилась в немецком журнале Chemie in unserer Zeit — в ней нет ничего, кроме заголовка и аннотации. По мнению ученых, маркировка «Chemical free» просто не имеет смысла, поэтому и обозревать в данном случае, строго говоря, нечего.
Вот тут можно прочитать эту статью за 6 долларов.
Френсис Крик и ДНК

Статья в Nature «Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid»
А вот за эти слова дали Нобелевскую премию:
«Мы не могли не заметить, что предложенное нами специфическое спаривание, непосредственно наводит на мысль о возможном механизме копирования генетического материала.»
«It has not escaped our notice that the specific pairing we have postulated immediately suggests a possible copying mechanism for the genetic material.»
Поведенческие науки
В 1974 году клинический психолог Деннис Аппер находился в творческом кризисе. Что-то мешало ему сесть и написать требуемую статью и он решил провести над собой научный эксперимент в надежде преодолеть «писательский блок». Результат опубликовал в престижном журнале Journal of Applied Behavioral Analysis:

Источники
- The Shortest Science Paper Ever Published Had No Words, and Was Utterly Brilliant
- «Без лишних слов»: самые короткие научные статьи
- Самые короткие научные статьи
- The Shortest Ever Papers — Numberphile
- Алексей Савватеев: «Последние прорывы в математике»
P.S.
Одно из недавних достижений в математике — решение задачи о разрезании равностороннего треугольника на 5 «равных» частей:
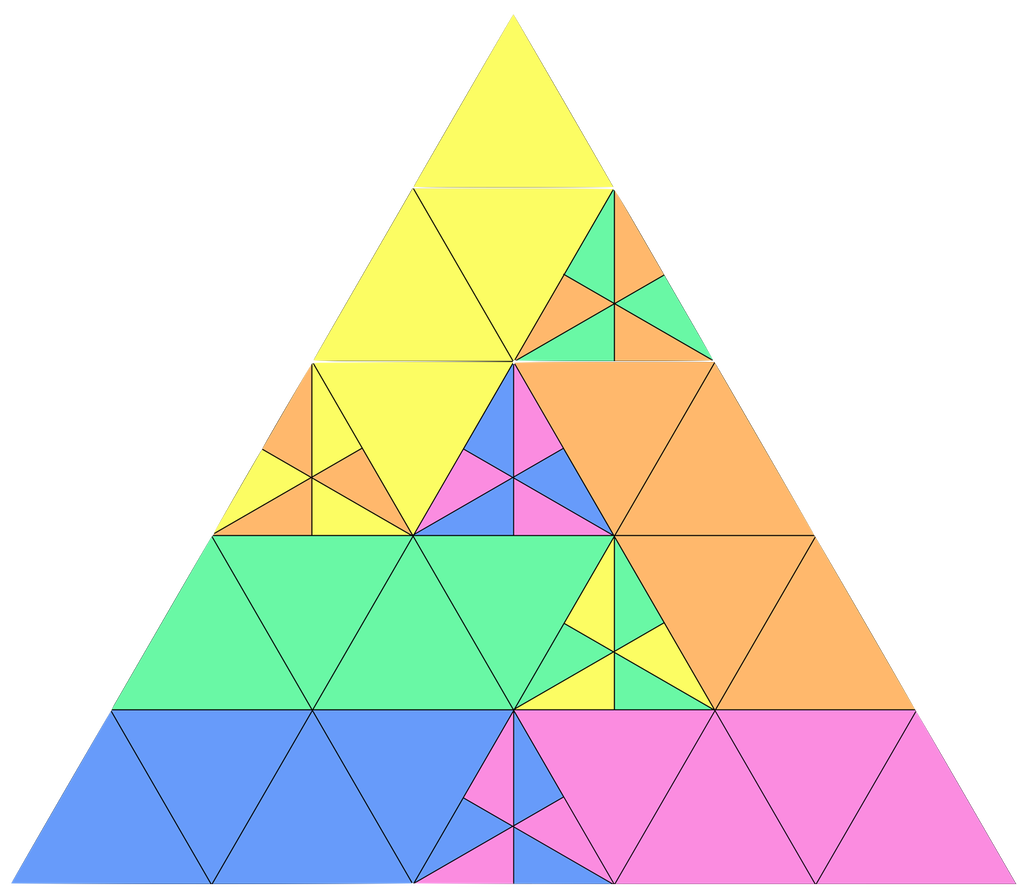
Цвет — это часть.
Only registered users can participate in poll. Log in, please.
Приходилось ли вам «раздувать» свои курсовые, дипломы, научные работы?
82.59% да593
15.04% нет108
2.37% другое17
718 users voted. 89 users abstained.