АES — американский стандарт шифрования. Часть II

Основные операции шифра

Рассматривая работу отдельных операций раунда, и повторяя раунды нужное число раз при этом иллюстрируя все промежуточные действия, а не только их конечные результаты, конкретным примером сообщения и ключа шифра мы в деталях наблюдаем все шаги процесса шифрования и можем анализировать, те условия при которых они реализуются, те результаты которые получаются и т.п. Помним при этом, что «дьявол кроется в деталях».

При слепом обращениях к имплементациям пользователь ничего этого не видит, не ощущает и главное — не понимает как шифрование происходит. Он задает только текст сообщения и ключ. Это все, что пользователю понятно. Пользователь целиком доверяет разработчику, на чем уже многократно попадались деятели от государственного уровня до рядовых пользователей. Это и прослушивание переговоров дипломатических представительств и отказ технических систем, когда чужое коммуникационное оборудование покупается и устанавливается без оглядки.
Как анализировать процесс шифрования, на что и как влияет внесение изменений не ясно.

Продолжая тему о блочном шифре — победителе конкурса, проводимого Национальным институтом стандартов и технологий США (1997 — 2000), будем рассматривать его функционирование, работу. Агентство национальной безопасности США не являлось участником конкурса, поэтому шансы стать победителем у разработчиков были велики.

Конкурсной комиссией были предварительно отобраны 15 заявок от разных стран. Выступать могли как организации, так и частные лица. В итоге победил RIJNDAEL(Бельгия) авторы Винсент Рюмен (Vincent Rijmen) и Ион Дэмен (Joan Daemen). Структуру шифра считают классической SP-сетью.

Ранее уже приводились основные технические характеристики и повторяться не будем.

Шифрование сообщений

Разработчиками создан шедевр, впервые идеология и реализация симметричного блочного шифра стала до конца понятной, так как шифр полностью основан на элементах классической (прозрачной) алгебраической структуры (поле), с достаточно скромными для обозрения количественными характеристиками. Конечное расширенное поле (поле многочленов) характеристики 2 имеет степень расширения n=8 и число элементов (порядок поля 2⁸ = 256), отсюда обозначение поля GF(2⁸).

Выбор неприводимого многочлена поля и примитивного элемента поля α = 00000011₂ = 3₁₀, также не является загадочным. Одним словом, это не DES и не отечественный ГОСТ 28147.89.
Исходные тексты подготавливаются на устройствах с клавиатурой, используя
Таблицу — Символы кода ASCII

Раунды и операции шифрования АЕS

Число раундов шифра обозначается Nr и зависит от длины ключа (Nr = 10 для ключа 128 битов, Nr= 12 для ключа 192 бита и Nr = 14 для ключа 256 битов).
Цикл (один раунд) шифрования AES состоит (в изменении состояния State шифруемого сообщения) из четырех основных операций:
1. AddRoundKey S + Ki; суммирование состояния (исходного текста с ключом)
2. SubBytes a∙x^-1 + b; замена результатов суммирования другими байтами
3. ShiftRows; S∙p(x); циклические сдвиги строк на разное число позиций
4. MixColumns A0∙S. перемешивание столбцов «квадрата».

Покажем, как это происходит на числовом примере для текущего состояния в каждой операции, начиная с верхней (нулевой) строки. Результаты 2-й и 3-й операций не требуют числовых преобразований, но MixColumns связана с умножением 2-х матриц и определение элементов результирующей матрицы требует конкретных вычислений в поле GF(2⁸). Алгоритм выработки ключа (Kеу Schedule) формирует 32-разрядные слова, число которых равно длине блока Nb.

Первому раунду предшествует предварительный (нулевой), в котором суммируются «квадраты» исходного текста и ключа. Рассмотрим каждую операцию более детально.

Существует анимация, поясняющая функционирование алгоритм шифра AES, весьма наглядно демонстрируются раундовые операции. Автор не ставил перед собой цели показать все детали процесса зашифрования, но даже этот упрощенный вариант (на уровне байтов), что почти совпадает с элементами поля GF(2⁸), удачно демонстрирует работу шифра AES. Детальное изложение для уяснения математических основ работы с элементами поля и конкретная реализация в различных представлениях элементов поля здесь.

Операция AddRoundKey для i-го раунда

Суммирование столбцов State с раундовым ключом (Add Round Key).

Раундовый ключ, предварительно вычисленный и выбранный, представляется в форме (квадрат) State (Key). Суммирование выполняется для одноименных столбцов. Пара столбцов State (Data) и State (Key) операцией XOR поразрядно складывается.

Таким образом, преобразование AddRoundKey состоит из суммирования матрицы S блока («квадрата 4×4») сообщения в M4(GF(2⁸)) с частичным Ki ключом i-го раунда (также с « квадратом 4×4 »). Результат суммирования обозначается SiA, т е. состояние после i-го AddRoundKey M4(GF (2⁸)) → M4(GF (2⁸)), S → SiA = S + Ki.
В начальном раунде (r = 0) выполняется только Add RoundKey – суммирование по mod2 (XOR) байтов блока данных и блока ключа. Результат этого раунда используется как исходное (State) состояние для первого раунда (r=1) и представляется в формате «квадрат».
Шифрование сообщений AES

Пример 1. Сообщение (исходный текст = ИТ) в 16-ричном представлении
имеет вид 32 43 f6 a8 88 5a 30 8d 31 31 98 a2 e0 37 07 34,
а ключ шифра 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 0f 4f 3c.
Операция AddRoundKey S + Ki для всех 16 байтов «квадрата» State
Предварительный раунд зашифрования подготавливает сумму ИТ с ключом.

Их Сумма, представленная байтами в формате «квадрат» при Nb = Nk = 4 и Nr = 10 имеет вид:


Рисунок Результат предварительного раунда (до первого)

Ключ и исходный текст (это может быть и звук и картинка и др.) представлены в 16-ричном виде. Это не самое удобное представление, поэтому преобразуем его к двоичным векторам и выполняем сложение по модулю 2.



Для удобства ручного счета 16-ричное представление байтов преобразуется в двоичное, а после суммирования обратный переход от двоичного к 16-ричному представлению.

Операция SubByte для i-го раунда

Замена байтов (Sub Bytes ( ) )

Первый раунд. Операция AddRoundKey уже выполнена. Все байты суммарного «квадрата» (исходного состояния обозначим их точками (х, y) на некоторой плоскости) преобразуются функцией S (x, y) в новые значения табличка "Замена байтов".

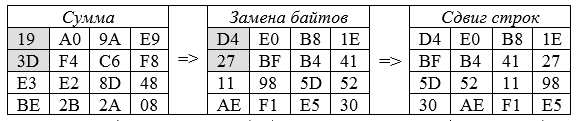
Заменяем угловой (левый верхний) байт State = Сумма, (равный 19), на байт d4 из таблицы замен S-блока и следующий (3D) на 27 (они выделены заливкой). Так преобразуются все 16 байтов квадрата "Сумма".

Так для первого байта {19} = {x, y}, x = 1, y = 9, S(19) = d4. Все такие значения также представляются «квадратом с замещениями».

Функция S (x, y) табулирована, т. е. задана таблицей с двумя входами – строка (х) и столбец (у). Поскольку все многообразие байтов исчерпывается числом 256, то таблица имеет размер 16×16 = 256, а ее строки и столбцы пронумерованы x, y = 0(1)15 цифрами 16-ричной системы счисления. Вид таблицы S (x, y) приведен ниже.



Покажем, как получены значения этой таблицы S (x, y). Вначале каждый байт исходного состояния {x, y} преобразуется в инвертированный {x, y}^-1, в мультипликативный обратный в поле GF(2⁸). Затем байт умножается на матрицу А. Нулевой байт переходит в себя {0, 0}^-1 = {0, 0}.

Каждая строка матрицы аффинного преобразования А содержит лишь пять единиц.

Затем к инвертированному (обращенному) байту применяют аффинное преобразование, которое в векторно-матричной форме записывается так



Аффинная матрица

Запись векторов сверху (младший разряд) вниз. Вектор сдвига c = {63}₁₆, что в таблице S (x, y) отражено для байта {00}. Каждый байт исходного состояния подвергается такому преобразованию, и их значения вписаны в квадратную таблицу S (x, y).

Скалярное представление аффинного преобразования имеет следующий вид (общий вид i -го элемента результата):


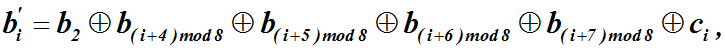
где ; , ^'– соответственно исходное и преобразованное значение i-го разряда байтов, i = 0(1)7.

Выражение для ^' содержит 6 слагаемых, так как каждая строка циклической матрицы аффинного преобразования имеет лишь 5 ненулевых элементов; шестое слагаемое берется из вектора сдвига ci.

Для ускорения вычислений используется квадратная таблица фиксированных значений (S (x, y) – блок). Значение b =’63’ – 16 — ричное число принадлежит GF(2⁸) и матрица а имеет вид, показанный ранее. В сущности, операция реализует подстановку (замену) байт из S «квадрата 16×16».

Преобразование SubByte состоит в применении к каждому элементу матрицы S элементарного преобразования s. Результат этой операции обозначается SiSu, т. е. это состояние блока текста после операции SubByte i-го раунда. Не путать буквы S и s (большую и малую).

В сущности, здесь выполняется аффинное преобразование с постоянным вектором сдвига, обозначаемым символом b
M4 (GF(2⁸)) → M4 (GF(2⁸)).

Запись векторов сверху (младший разряд) вниз. Вектор сдвига c = {63}₁₆, что в таблице S (x, y) отражено для байта {00}. Каждый байт исходного текста (состояния) подвергается такому преобразованию, и их значения вписаны в таблицу S (x, y).

Пример 2. Первый байт исходного состояния первого раунда равен {19}. Мультипликативный обратный для него (см. Табл. П1) равен 3f = {19}^-1= 0011 1111₂ =α¹¹³. Это значение легко находится по таблице элементов поля GF(2⁸). При отсутствии таблицы элементов поля можно выполнить и непосредственные вычисления.

Пусть байт {x, y} = 09 =α ¹⁹⁹ и {09} ^-1 = 4f, тогда
b0 = (1+0+1)mod2 = 0, b4 = (1+1+0)mod2 = 0,
b1 = (1+0+1)mod2 = 0, b5 = (0+1+1)mod2 = 0,
b2 = (1+0+0)mod2 = 1, b6 = (0+1+1)mod2 = 0,
b3 = (1+1+0)mod2 = 0, b7 = (0+1+0)mod2 = 1.
Результирующий вектор ( 0, 1, 2, 3, 4, 5, 6, 7) =1000 0100₂ = 84.

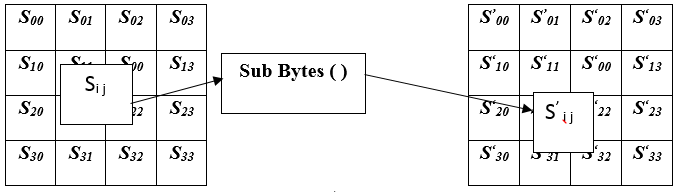
Следовательно, байт 4f S-блоком преобразуется в байт 84, что можно увидеть в таблице замен S (x, y) = S (4, f) = 84. Этот результата лежит на пересечении строки с номером 4 и столбца с номером f. Геометрическое представление замены байтов (SubBytes) изображено на рисунке 4, где s нелинейное преобразование, определяемое соотношениями:
GF(2⁸) → GF(2⁸),

Операция ShiftRows для i-го раунда

В каждом раунде после замены всех байтов State получен квадрат (средний) исходного состояния для преобразования сдвига строк. Такой сдвиг способствует еще большему перемешиванию данных.

Выбор величин сдвигов подчинен следующим условиям:
Каждая строка должна иметь индивидуальное смещение элементов;
Реализация операции должна быть простой;

Совокупность сдвигов наилучшим образом должна препятствовать проведению атак:

А) атак, использующих сокращенные дифференциалы
В) атак типа Square.


Рисунок 5 Состояние после сдвига строк

ShiftRows преобразование – перемещения байтов строки в матрице состояния S, которое циклически сдвигает строки матрицы состояния на различные по величине смещения. Результат операции обозначается SiSh, т. е. это состояние после операции ShiftRows
i-го раунда. Такие перемещения могут быть описаны Р(х) перестановкой байт из «квадрата» S, которая имеет вид:


Из всех вариантов сдвигов, обеспечивающих наилучшее противостояние атакам, был выбран самый простой – циклический сдвиг и c0 = 0.

Геометрическое представление преобразования замены байтов изображено на рисунке 4, где приведены квадраты числового примера для первого раунда.

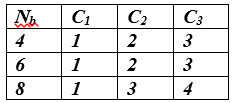
Сдвиг строк в массиве State выполняется влево. Строка с номером нуль остается неподвижной (не сдвигается). Остальные строки RIJNDAEL сдвигаются на число байтов c1, c2, c3, указанное в квадрате на рисунке 5), в зависимости от числа Nb байтов в блоке данных. Строка 1 сдвигается на c1 байтов, строка 2 на c2 байтов и строка 3 на с3 байтов.

В стандарте AES величина Nb = 128 постоянная, поэтому всегда c1 = 1, c2 = 2 и c3 = 3.

Таблица Величины сдвигов

Операция MixColumns для i-го раунда

Это преобразование применяется для обеспечивания рассеивания символов исходного сообщения, удовлетворения второго после перемешивания требования к шифрующим преобразованиям. Требования к такому преобразованию, предъявляемые теорией синтеза шифров, следующие.

• Обратимость получаемого результата.
• Линейность в поле GF(2⁸); выполнение этого требования создает условия для применения алгоритма прямого расшифрования.
• Достаточно сильное рассеивание данных.
• Высокую скорость реализации на 8-разрядных процессорах; единообразие обработки любых блоков данных, т. е. симметричность.
• Простой вид для описания и реализации.

Все названные требования удовлетворены в стандарте АES. Из возможных линейных преобразований 4 bytes → 4 bytes выбрана операция умножения многочленов (элементов поля) по модулю ψ(x) = x⁴ + 1. Выбор коэффициентов сомножителей обусловлен требованиями 1, 3 и 4. Коэффициенты {00}, {01}, {02}, {03},… соответствуют: {00} – отсутствию преобразования; {01} – не требуется умножения; {02} – умножение при использовании функции x time ( ) и {03} – при использовании x time и последующего сложения по mod2 промежуточных результатов.

По другим, не менее важным сообщениям, выбор коэффициентов был остановлен на приведенных выше значениях.

Сущность преобразования Mix Columns ( ) состоит в следующем. Столбцы State
S = < S0c, S1c, S2c, S3c>, с = 0(1)3, после сдвига строк рассматриваются как элементы поля GF(2⁸) и умножаются по mod(x⁴ + 1) на фиксированный многочлен g(x):
g(x) = {03}x³+{0,1}x²+{01}x+{02}.


где с – номер столбца State, c = 0(1)3.

где А – циркулянтная матрица, т. е. линейное инвертируемое (обратимое) отображение на GF (2⁸), А принадлежит M8(GF (2⁸)),
× – обозначает умножение матрицы из GF (2⁸) и вектора
х -1 = {b0 b1…b7 }b, который рассматривается как элемент над полем GF(2) – векторного пространства, эквивалентный транспонированному в вектор {b0 b1…b7 }b.

Развернем это выражение в скалярную форму
S’0C = ({02}· S0C) ⊕ ({03}· S1C) ⊕ S2C ⊕ S3C;
S’1C = S0C ⊕ ({02}· S1C) ⊕ ({03}· S2C) ⊕ S3C;
S’2C = S0C ⊕ S1C ⊕ ({02}·S2C) ⊕ ({03}· S3C);
S’3C = ({03}· S0C) ⊕ S1C ⊕ S2C ⊕ ({02}· S3C).
В результате выполнения указанных действий байты вектора
SC = <S0c, S1c, S2c, S3c> будут заменены байтами S’0C, S’1C, S’2C, S’3C.

MixColumns преобразование состоит из умножения двух матриц. Матрицы S промежуточного состояния текста и фиксированной матрицы A0 обе из введенного ранее множества M4 (GF (2⁸)). Результат операции обозначается символом SiM, это по существу состояние S после операции MixColumns i-го раунда.

M4 (GF (2⁸)) → M4 (GF (2⁸)),
S → Si, М = А·S,
где матрицы А и А^-1 (циркулянтные матрицы) определяются как:

.
Операция MixColumns – произведение специальной цикловой А0 матрицы на матрицу State, по правилу «строка на столбец»

.
Два пустых столбца в результирующей матрице оставлены для самостоятельного заполнения.
Начинаем с левого углового элемента нулевой строки квадрата. Его значение определяется суммой произведений пар элементов: {02}D4⊕{03}BF ⊕ {01}5D ⊕ {01}30. Элементы обеих матриц — это элементы поля GF(2⁸) с одной стороны и информационные байты в 16-ричном представлении – с другой. Умножение элементов в поле удобно выполнять в степенном представлении примитивного элемента.

Пользуясь таблицей поля, выполним замену 16-ричного представления на степенное для левой цикловой матрицы элементы {01} = a⁰, {02} = a²⁵, {03} = a¹. Для правой матрицы в произведении получим


Теперь можно переписать сумму для углового элемента и остальных в строке через степени примитивного элемента расширенного поля, слагаемые разместим в колонках таблицы.
Результаты суммирования помещаем в последней строке таблицы для каждой строки матрицы перемешанных столбцов.

1-й элемент нулевой строки определяется в виде:

{02}D4⊕ {03}BF ⊕ {01}5D ⊕ {01}30 = a²⁵а⁶⁵⊕ a¹а¹⁵⁷⊕ a⁰а¹³⁶⊕ a⁰а¹⁰¹ = а⁹⁰⊕ a¹⁵⁸⊕а¹³⁶⊕а¹⁰¹,

2-й элемент нулевой строки определяется аналогичным соотношением (поменялся столбец)

{02}Е0⊕{03}B4⊕ {01}52⊕ {01}АЕ = a²⁵а⁶⁸⊕ a¹а²⁵¹⊕ a⁰а²⁵³⊕ a⁰а¹²³ = а⁹³⊕ a²⁵²⊕ а²⁵³⊕а¹²³,

3-й элемент нулевой строки определяется аналогичным соотношением поменялся столбец

{02}B8⊕{03}41⊕ {01}11⊕ {01}F1 = a²⁵а⁵⁹⊕ a¹а¹⁴³⊕ a⁰а⁴⊕ a⁰а⁷⁴ = а⁸⁴⊕ a¹⁴⁴⊕ а⁴⊕ а⁷⁴,

4-й элемент нулевой строки определяется аналогичным соотношением поменялся столбец

{02}1Е⊕{03}27⊕ {01}98⊕ {01}Е5 = a²⁵а²⁸⊕ a¹а¹⁰⁶⊕ a⁰а⁸⁹⊕ a⁰а³² = а⁵³⊕a¹⁰⁷⊕ а⁸⁹⊕а³².

Показатели степеней просто суммируются при перемножениях как логарифмы. Суммирование слагаемых удобно выполнить возвратом к 16-ричному, а от него к двоичному представлению. Опять воспользуемся таблицей элементов поля GF(2⁸).



Перейдем к вычислению элементов 1-й строки матрицы (изменяется номер строки циклической матрицы) Элементы в парах произведений изменяются относительно 0-й строки.

1-й элемент 1-й строки матрицы перемешанных столбцов определяется соотношением.


Перейдем к вычислению элементов 2-й строки матрицы (изменяется номер строки циклической матрицы). Элементы в парах произведений изменяются относительно 1-й строки.

1-й элемент 2-й строки матрицы перемешанных столбцов определяется соотношением



Перейдем к вычислению элементов 3-й строки матрицы (изменяется номер строки циклической матрицы) Элементы в парах произведений изменяются относительно 2-й строки.