Мы уже решали задачу коммивояжёра точно методом динамического программирования. С тех пор прошло немало времени. Мне бы хотелось поделиться некоторыми соображениями по улучшению алгоритма, а также представить алгоритм пригодный для расчёта задачи коммивояжера на GPU.

Динамическое программирование — это метод решения сложных задач путём разбиения их на более мелкие подзадачи, решение которых легче и проще.

Основная идея метода заключается в том, чтобы не решать одну и ту же подзадачу многократно, а сохранять результаты решения подзадач и повторно использовать их для ускорения общего процесса решения.

Задача о сумме подмножеств в общей формулировке звучит так:

Существует множество S чисел, вопрос состоит в том, будет ли сумма некоторого подмножества от S равна заданному числу Т.

Известно, что данная задача NP-полная.

Мы будем решать эквивалентную задачу, где все числа являются натуральными.

Частным случаем задачи о сумме подмножеств является задача разбиения множества чисел:

Множество чисел S необходимо разбить на два подмножества S1 и S2, где сумма S1 равна сумме S2.

(От задачи о сумме подмножеств текущая отличается только тем, что T = SUM(S1) / 2 = SUM(S2) / 2)

Хочу предложить вам простой и элегантный способ относительно быстрого решения обеих задач методом целочисленного линейного программирования (ЦЛП). Мы получим не только точный ответ на вопрос, но и найдём искомое подмножество.

Если вам нужно решить задачу коммивояжёра, то нет ничего проще. Нужно просто взять квантовый компьютер с числом кубитов не меньшим числа вершин рассчитываемого графа…

Нет под рукой квантового компьютера? Не беда, читайте дальше и узнаете, как можно решать данную задачу на классическом компьютере за полиномиальное время* от числа вершин.

И снова здравствуйте, уважаемые читатели Хабра. Мы продолжаем наше путешествие в мир алгоритмов поиска оптимального пути.

В прошлой работе мы уже узнали, как можно найти оптимальный путь в графе в несколько сотен вершин. В данной работе хочу более подробно остановится на сути метода, а также разобрать возможность по его ускорению на графах от тысячи элементов.

Дочитав эту статью до конца, вы сможете решать точно задачу коммивояжёра на сотню элементов за считанные секунды!

Заинтригованы? Тогда, добро пожаловать под кат.

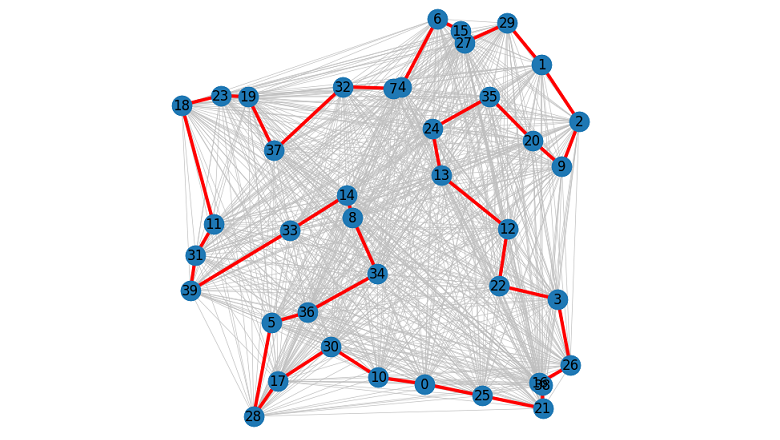
Что делает код хорошим? Большинство программистов ответят: хороший код должен быть структурирован, легко читаем и понятен. Но так ли важно качество кода, если он медленный? В большинстве задач производительность кода не критична, хотя и желательна. Но есть задачи, время выполнения которых столь огромно, что выигрыш в производительности доминирует над всем остальным.

Я говорю про NP-трудные задачи (NP-трудность - недетерминированная полиномиальная трудность по времени) и на одной из данного класса хочу акцентировать ваше внимание. Задаче коммивояжера.

Мы не будем рассматривать эвристические алгоритмы, нам нужно точное решение.

Задача коммивояжёра – одна из интереснейших подзадач комбинаторной оптимизации. Впервые мне пришлось с ней столкнуться, работая над логистической системой торгового предприятия.

Решение методом грубой силы не подходило из-за вычислительной сложности. Была предпринята попытка реализовать метод ветвления и границ с отсечением в глубину. В целом, подход себя оправдывал, но иногда при некоторых специфических входных данных алгоритм выдавал решение далёкое от оптимального.

Типичный маршрут доставки товара предприятия состоял из пары десятков точек, изредка доходящий до 25-26. Матрица расстояний рассчитывалась с помощью алгоритма Дейкстры. Дальше нужно было выбрать оптимальный маршрут из возможных.

Иногда отражение в зеркале более реально, чем сам объект…
— Льюис Кэрролл (Алиса в зазеркалье)

Assembler – мой любимый язык, … но жизнь так коротка.