Comments 109
Выглядит круто, а теперь вопрос, разрешима ли задача определения, пересекаются ли (ну или касаются) две фигуры друг друга? Пусть даже вторая для простоты будет отрезком.
Понадобится примитив проверки, пересекаются ли два отрезка. Соответственно смотрим, пересекается ли второй отрезок хоть с одной стороной многоугольника. Если да, то задача решена — ответ ДА. Если нет, то либо отрезок находится целиком вне фигуры, или целиком внутри. Это проверяется тестом на принадлежность фигуре одного из концов отрезка. Если принадлежит, то ответ — ДА, иначе — НЕТ.
Я может быть понял неправильно, но Вы хотите сказать, что пересечение отрезка и фигуры можно определить проверив принадлежность фигуре его концов?
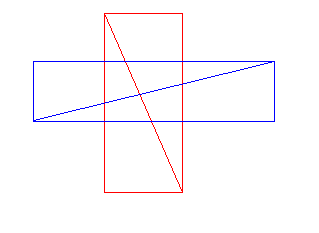
Нет, смотрите. Есть три базовых случая — отрезок пересекает границу, отрезок не пересекает границу и целиком лежит в фигуре, и отрезок не пересекает границу и лежит вне фигуры:
Первый случай проверяется наличием пересечения отрезка с границами многоугольника. Второй и третий различаются по наличию одного из концов отрезка внутри многоугольника.
Первый случай проверяется наличием пересечения отрезка с границами многоугольника. Второй и третий различаются по наличию одного из концов отрезка внутри многоугольника.
Хм…
Спасибо за вопрос, первое, что приходи на ум – разбить отрезок на точки с каким-то шагом и проверять их вхождение. Но чувствую, что это некрасиво и очень не оптимально. Подумаю над аналитическим решением.
Спасибо за вопрос, первое, что приходи на ум – разбить отрезок на точки с каким-то шагом и проверять их вхождение. Но чувствую, что это некрасиво и очень не оптимально. Подумаю над аналитическим решением.
Првое что мне пришло на ум: разбить фигуру на выпуклые многоугольники(либо треугольники) а далее вхождение точки в выпуклую фигуру(а это проще простого).
Как разрешится такой пример?
Вхождение точки в выпуклую фигуру — да, проверяется очень просто.
А вот триангуляция произвольного полигона в общем случае — не такая уж тривиальная задача, как может показаться на первый взгляд.
А вот триангуляция произвольного полигона в общем случае — не такая уж тривиальная задача, как может показаться на первый взгляд.
надеюсь, не ошибусь, если скажу, что в современной компьютерной графике графическим примитивом как раз является треугольник. из его преимуществ, помимо прочего, то что сумма углов его всегда 180, это выпуклая фигура и он всегда однозначно определяет плоскость, что удобно в трехмерных преобразованиях.
Как по мне, то намного проще проверить пересечение отрезка с каждой линией контура. Пересекает хоть одну линию контура — вуаля. Ну еще нужна проверка того, что весь отрезок целиком не лежит внутри полигона (тогда нет пересечения с линией контура, но отрезок внутри) — любой из концов отрезка проверить лежит внутри полигона или нет.
З.Ы. Надеюсь не надо рассказывать как проверить пересекаются ли 2 отрезка.
З.Ы. Надеюсь не надо рассказывать как проверить пересекаются ли 2 отрезка.
С познавательной точки зрения подход, определённо, интересный, но на практике есть более быстрый и надёжный алгоритм. Считается количество пересечений горизонтального луча из точки с рёбрами полигона. Чётное число пересечений — точка снаружи, нечётное — внутри. Этот алгоритм более быстрый, т.к. для определения факта пересечения луча и отрезка не требуется считать тангенсы, и даже можно обойтись без деления. А более надёжный, т.к. факт пересечения можно определить с абсолютной точностью (т.е. нет погрешности, этого >eps).
насколько я помню, это только для выпуклых многоугольников
Не обязательно.
Нарисуйте на листике просто пару многоугольников и проверьте.
С выпуклым это вообще не задача.
С выпуклыми многоугольниками всё еще проще.
Достаточно проверить с какой стороны относительно каждого ребра лежит точка. Как только обнаруживается ребро, относительно которого точка лежит с противоположной стороны, можно перебор прекращать, так как точка за пределами многогранника. Соответственно, если точка лежит по одну сторону от всех рёбер, то она лежит внутри.
Сторона определяется знаком векторного произведения (P2 — P1)^(P — P1), где Pi — точки многогранника, а P — тестируемая точка.
Достаточно проверить с какой стороны относительно каждого ребра лежит точка. Как только обнаруживается ребро, относительно которого точка лежит с противоположной стороны, можно перебор прекращать, так как точка за пределами многогранника. Соответственно, если точка лежит по одну сторону от всех рёбер, то она лежит внутри.
Сторона определяется знаком векторного произведения (P2 — P1)^(P — P1), где Pi — точки многогранника, а P — тестируемая точка.
Кстати, при нуле пересечений возникает неопределенность и требуется выбрать другое направление луча
Да нет, если ноль пересечений, то точка лежит вне полигона.
Неопределенность возникает, если луч пересекает вершину невыпуклого полигона. Проще всего такие пересечения не считать, но тогда может возникнуть ноль пересечений даже если точка внутри. Вот пример:
Красный луч — два пересечения, но точка внутри полигона. Для устранения ошибки достаточно не считать пересечение с вершиной. Но тогда получаем следующее. Синий луч — одно пересечение с вершиной. Вершину не считаем, итого ноль пересечений.
Вот вам и неопределенность
Красный луч — два пересечения, но точка внутри полигона. Для устранения ошибки достаточно не считать пересечение с вершиной. Но тогда получаем следующее. Синий луч — одно пересечение с вершиной. Вершину не считаем, итого ноль пересечений.
Вот вам и неопределенность
Значит не считать вершину — плохая идея, и не считать пересечения с вершиной всё-таки недостаточно :)
Более того, есть еще случай, когда все ребро лежит на луче, его тоже неплохо было бы рассмотреть отдельно.
Более того, есть еще случай, когда все ребро лежит на луче, его тоже неплохо было бы рассмотреть отдельно.
Не считать вершину — простейшее решение, причем полное. Единственный недостаток — необходимость пуска другого луча в случае неопределенности.
Ребро лежит на луче — это интересный случай, его разрешение зависит от того, считать точку, лежащую на ограничивающей кривой, принадлежащей фигуре. Если да — то случай сводится к лучу, проходящему через вершину (для его разрешения возможны варианты), если нет — то вершину не считаем.
По другому варианту, не требующему повторного пуска луча, в точке пересечения нужно считать производную функции полигона (для полигона весьма тривиальная задача), если она равна нулю — то вершина есть экстремум и ее считать не надо.
Ребро лежит на луче — это интересный случай, его разрешение зависит от того, считать точку, лежащую на ограничивающей кривой, принадлежащей фигуре. Если да — то случай сводится к лучу, проходящему через вершину (для его разрешения возможны варианты), если нет — то вершину не считаем.
По другому варианту, не требующему повторного пуска луча, в точке пересечения нужно считать производную функции полигона (для полигона весьма тривиальная задача), если она равна нулю — то вершина есть экстремум и ее считать не надо.
Это не проблема. Если касание мы считаем пересечением, то тут два пересечения в точке касания, и на четность не повлияет. Если не считаем, то ноль пересечений в точке касания и тоже не повлияет на четность.
Алгоритм в итоге сводится к проверке не лежит ли точка на границе полигона, а если нет, то просто считаем число пересечений. Касания вершин считаем либо за два пересечения, либо за ноль. Не важно какой из двух вариантов выберем.
А вы почему-то предложили касание считать один раз, но ведь касание луча присходит с двумя отрезками (рёбрами, сторонами).
А алгоритмически как это сделать? Как различить случаи, нарисованные выше?
Вот тут детально изложено: https://en.wikipedia.org/wiki/Point_in_polygon
Более универсальным и простым решением будет https://en.wikipedia.org/wiki/Winding_number
Прямо привет из прошлого )
Если считать что за ноль, что за 2 - получится четное количество пересечений для синего луча
Да, лучше, конечно, для определения внутри или снаружи полгона использовать алгоритм https://en.wikipedia.org/wiki/Winding_number
Если луч попадает в вершину, смотрим другие концы сторон при этой вершине: по одну они сторону от луча или по разные.
Простите, не Вам
Описанный в комментарии алгоритм действительно только для выпуклых. Для любых многоугольников нужно отсеивать пересечение луча с вершинами полинома
Луч может быть и не горизонтальный, а вообще в любую сторону — правильно я понял?
Да, но важно не попасть лучом в вершину многоугольника. Я лично пускал 3 (три) рандомных луча, 3 одинаковых (с точки зрение четности\нечетности пересечений) результата даёт судить о их верности с достаточной вероятностью.
Ну можно и с попадением. Только тогда надо считать отрезки полуоткрытыми и аккуратно разбираться с точностью, если координаты нецелые.
Вопрос на засыпку. Какова эта вероятность? Вот пример, где Ваша программа ошибается
Не надо бояться попасть в вершину. Там всё просто. Если луч проходит через вершину (а в вершине сходится два отрезка), то он либо две стороны пересекает либо ноль. Это не важно для алгоритма, лишь бы мы везде одинаково это воспринимали. Например везде считать, что край отрезка входит в отрезок. Это значит касание луча вершины всегда будет добаалять 2 пересечения.
правильно. Ведь вы можете повернуть не ось, а фигуру, результат не изменится
Удобнее ортогональный луч пускать, но да, не важно в какую сторону, хоть по диагонали.
Ортогональный удобнее потому, что пересечения искать легче.
Кстати, есть ешё интересный кейс когда одна из граней лежит на нём частично или полностью.
Но такой кейс тоже легко решается. Алгоритм примерно такой: перебираем все грани и считаем число пересечений луча с каждой гранью.
Считаем сколько концов грани лежит на луче. К этому числу прибавляем 1, если грань пересекается с лучом не будучи параллельной ему.
Суммируем для каждой грани и проверяем на четность. Всё.
Проблем не будет. Представьте, что горизонтальный луч приподнят на бесконечно малую величину. Тогда если обе вершины ребра лежали на прямой луча, ребро станет параллельно лучу (нет пересечения). Если ребро касалось луча верхней вершиной — касание исчезнет (опять нет пересечения). Наконец, если ребро касалось луча нижней вершиной касание превратится в пересечение. Алгоритмически это выглядит просто как засчитывание пересечений только когда ребро либо явно пересекает луч, либо касается его нижней вершиной.
Если координаты вершин целочисленные, луч может идти с наклоном 2^0.5, такой луч не пересекает целочисленных точек
поясните пожалуйста, про лучи. как их правильно рисовать?
есть более подробное описание метода?
есть более подробное описание метода?
А математическое обоснование есть или выведено опытным путем?
Мне достаточно интуитивного. Замкнутая кривая пересекается, например (без потери общности), горизонтальной прямой чётное число раз, касания не рассматриваем, применяя всё то же поднятие прямой на бесконечно малую величину (см. выше). Для кривой без самопересечений (а именно такие ограничивают полигон) пары точек вдоль горизонтальной оси ограничивают отрезки прямой внутри области. Некоторая точка разбивает прямую на два луча. И либо на обоих лучах будет чётное число точек пересечения, что означает что точка не попала между пары точек, задающих отрезок внутри области. Либо на обоих лучах будет нечётное число точек пересечения, и значит точка попала на отрезок внутри области, а значит и в саму область.
Математическое обоснование ровно такое же, как и у теоремы интегрирования Гаусса (хотя она может носить и любое другое название). Возьмем, например, заряд и сферу. Если заряд находится внутри, поток поля будет ненулевым. Если снаружи — понятно, общий поток сведется к нулю.
А в этом случае у нас тоже самое на плоскости — теорема Стокса (хотя, вообще говоря, обе теоремы — частные случаи обощенной формулы Стокса для дифференциальных форм).
Возможно, связь основных векторных теорем и лучей в случайные стороны неочевидна на первый взгляд, но все так :) А насчет крайнего случая с попаданием луча в вершину — так в математике такого не бывает))
А в этом случае у нас тоже самое на плоскости — теорема Стокса (хотя, вообще говоря, обе теоремы — частные случаи обощенной формулы Стокса для дифференциальных форм).
Возможно, связь основных векторных теорем и лучей в случайные стороны неочевидна на первый взгляд, но все так :) А насчет крайнего случая с попаданием луча в вершину — так в математике такого не бывает))
> А насчет крайнего случая с попаданием луча в вершину — так в математике такого не бывает))
Это почему, простите?
Это почему, простите?
Неосторожно ляпнул. Имел в виду тот случай с теоремой Гаусса, когда мы рассматриваем гладкую замкнутую поверхность и некий луч, проходящий касательно снаружи нее. Эта точка ведь просто не попадает в поток.
Так будет лучше?
Так будет лучше?
Намного. Хотя здесь не совсем корректно сравнение с теоремой Гаусса, поскольку в ее формулировке используется понятие заряда внутри поверхности, т.е. определено замкнутое множество точек, или другими словами, заряд на самой поверхности не рассматривается. Применительно к рассматриваемой задаче мы не можем пренебрегать точками, лежащими на ограничивающей кривой.
Хотя, в общем, это вопрос терминологии — считать ли точку на ограничивающей кривой лежащей внутри фигуры. В теории обычно — нет, на практике чаще всего — да.
Хотя, в общем, это вопрос терминологии — считать ли точку на ограничивающей кривой лежащей внутри фигуры. В теории обычно — нет, на практике чаще всего — да.
Моя аналогия пришла еще и от детского объяснения Гаусса. Когда вводят линии поля, каждая из которых пересекает поверхность четное или нечетное количество раз, а плотность их падает с расстоянием — потому они компенсируются, если точка снаружи.
Знаете, это все довольно забавно. Изначально задача относится к прикладным задачам численных методов (назовем это так — хотя бы потому что речь идет о решении ее на компьютере), автор статьи решил очень успешно приткнул теорию функций комплексной переменной, а мне все электродинамика мерещится :)
Знаете, это все довольно забавно. Изначально задача относится к прикладным задачам численных методов (назовем это так — хотя бы потому что речь идет о решении ее на компьютере), автор статьи решил очень успешно приткнул теорию функций комплексной переменной, а мне все электродинамика мерещится :)
По мне решение автора весьма остроумное и вполне имеет право на жизнь. Так что может векторный анализ вкупе с дифференциальной геометрией подкинет методу. Интересно, кстати, что решение автора распространяется на любые плоские фигуры, не только полигоны
Меня не оставляет ощущение, что я о чем-то таком тоже думал — поэтому я в восторге от решения. Хоть оно и медленнее других, но оно использует свойства нашего пространства — самые основные законы природы.
Точно также меня беспокоит идея интегрирования по произвольным н-мерным многообразиям с помощью дифференциальных форм и обобщенной формулы Стокса — уж больно элегантно и соблазнительно выглядит оператор границы. Но если мы возьмем хотя бы н-мерную сферу — хороший метод через квадрат интеграла Пуассона или плохой через н-мерный якобиан сферических координат окажутся во многие-многие разы быстрее. Потому что внешние формы сильно связаны с определителями, а определитель — уж очень дорогая операция.
Точно также меня беспокоит идея интегрирования по произвольным н-мерным многообразиям с помощью дифференциальных форм и обобщенной формулы Стокса — уж больно элегантно и соблазнительно выглядит оператор границы. Но если мы возьмем хотя бы н-мерную сферу — хороший метод через квадрат интеграла Пуассона или плохой через н-мерный якобиан сферических координат окажутся во многие-многие разы быстрее. Потому что внешние формы сильно связаны с определителями, а определитель — уж очень дорогая операция.
Мне кажется, что овчинка стоит выделки. В конце концов дороговизна отдельной операции — ничто по сравнению с многообразием применений. В моей практике попадались задачи, где как раз требовалось определить факт попадания точки внутрь области, ограниченной кривой в N-мерном пространстве. Я их решал аппроксимацией полигоном и подсчетом углов, но не оставляло ощущение «костыля». Так что наработки в области интегрирования по многообразиям могут оказаться очень востребованными
Ага. Простейшая задача «Обрезка карты по границе области».
Оперирует цифрами порядка:
— тысяча точек в полигоне границы
— 5-6 миллионов точек всего
— 3-4 миллиона точек попадает в границы
Сами посчитаете количество операций на решение?
Оперирует цифрами порядка:
— тысяча точек в полигоне границы
— 5-6 миллионов точек всего
— 3-4 миллиона точек попадает в границы
Сами посчитаете количество операций на решение?
Не понял, о чём речь.
1. Обрезка, оно же отсечение — это совсем другая задача, решается другими алгоритмами.
2. Судя по тому, что 3-4 млн. точек из 5-6 млн попадает на границы — имеются ввиду не точки, а пикселы. А в статье решается непрерывная задача. Для дискретных задач, опять же есть другие алгоритмы.
1. Обрезка, оно же отсечение — это совсем другая задача, решается другими алгоритмами.
2. Судя по тому, что 3-4 млн. точек из 5-6 млн попадает на границы — имеются ввиду не точки, а пикселы. А в статье решается непрерывная задача. Для дискретных задач, опять же есть другие алгоритмы.
Географическая карта. Объекты — точки заданные координатами. Соответственно задача именно такая — определисть попадание в полигон. Дальше — или забыть, или перенести в результат.
И попадают не «на границы», а в «границы» — т.е. должны оказаться в результирующем наборе.
Соответственно по алгоритму «сканирующей прямой» для того чтобы определить что точка нам нужна/не нужна необходимо сделать количество_проверок = количество_точек * количество_рёбер_границы
И это количество одинаково как для случая попадания, так и для случая непопадания.
В реальных условиях это непозволительные затраты.
И попадают не «на границы», а в «границы» — т.е. должны оказаться в результирующем наборе.
Соответственно по алгоритму «сканирующей прямой» для того чтобы определить что точка нам нужна/не нужна необходимо сделать количество_проверок = количество_точек * количество_рёбер_границы
И это количество одинаково как для случая попадания, так и для случая непопадания.
В реальных условиях это непозволительные затраты.
Ясно. Согласен, что прямое решение для такой задачи работает медленно. Обычно, когда данных много применяют какую-то пространственную иерархию (дерево, сетку и т.п.). И сначала определяют как узел иерархии соотносится с областью — если он полностью внутри или снаружи, то его внутренние элементы можно дальше не проверять. А вот если узел лежит в области частично, то в любом случае придётся использовать точную проверку для всех элементов этого узла.
На самом деле, случай с картами можно (с натяжкой) считать дискретным, т.к. используется определенная точность (скажем, до 1е-5, хотя в NASA все вычисления проводятся до 1е-16).
Количество_проверок == количество_ребер, и вот почему. Например, луч ориентирован вправо. Для каждого отрезка границы (ребра) нужно найти точку пересечения прямой-продолжения луча и прямой-продолжения отрезка, и проверить принадлежность этой точки лучу и отрезку, что делается довольно просто за О(1). Таким образом, алгоритм не зависит от количества_точек как параметра.
Количество_проверок == количество_ребер, и вот почему. Например, луч ориентирован вправо. Для каждого отрезка границы (ребра) нужно найти точку пересечения прямой-продолжения луча и прямой-продолжения отрезка, и проверить принадлежность этой точки лучу и отрезку, что делается довольно просто за О(1). Таким образом, алгоритм не зависит от количества_точек как параметра.
Тангенсы можно высчитывать по таблице, в математических библиотеках так и сделано, кажется, но можно и самому сделать, т.е. на них скорость уже не потеряем. Ну и как сказано уже, ваш подход только для выпуклых многоугольников.
работает для любого многоугольника.
Хорошо, тогда почему у меня и у точки снаружи и у точки внутри по 4 пересечения с ребрами у горизонтального луча, и по 6 если и горизонтальный и вертикальный провести?
Где ошибка?
>>Считается количество пересечений горизонтального луча из точки с рёбрами полигона. Чётное число пересечений — точка снаружи, нечётное — внутри.
Где ошибка?
>>Считается количество пересечений горизонтального луча из точки с рёбрами полигона. Чётное число пересечений — точка снаружи, нечётное — внутри.
Абсолютно верно, более того, подсчётом пересечений и касаний можно определить находится ли точка внутри вообще любой фигуры, необязательно многогранника.
А по-моему еще проще — через площадь. Если сумма площадей треугольников, которые построены на ребрах полигона и заданной точке, равна общей площади полигона — следовательно, точка лежит внутри. Алгоритм также работает и для не выпуклых многоугольников, сложность — линейная, равно как и в Вашем подходе. Да, кстати, насчет «более быстрый» — это будет мало ощутимо. Сложность будет тех же О(N), просто константа побольше. Впрочем, конечно же, если можно сократить константу — почему бы этого не сделать? :)
Насчет абсолютной точности — я с Вами не соглашусь. С чем я могу согласиться, так это с тем, что координаты пересечения луча и отрезка вычисляются достаточно точно (гораздо точнее, чем использование тангенсов), но я пока не представляю себе, как вы решили избавиться от eps в вычислительной геометрии — буду рад услышать ответ.
Насчет абсолютной точности — я с Вами не соглашусь. С чем я могу согласиться, так это с тем, что координаты пересечения луча и отрезка вычисляются достаточно точно (гораздо точнее, чем использование тангенсов), но я пока не представляю себе, как вы решили избавиться от eps в вычислительной геометрии — буду рад услышать ответ.
Протест и баста! :)
Окей, вот вам тест для формы Н: нашу точку выносим «далеко-далеко». Тогда сумма площадей треугольников будет, очевидно, «очень-очень большой», а площадь самой буквы Н — сравнительно маленькой.
Возможно, вы имели ввиду ориентированную площадь? В таком случае да, он не всегда сработает вообще. Но для абсолютных (неотрицательных) площадей такой алгоритм, кажется, должен работать.
И еще: плюс такого подхода не только в быстроте работы, а и в быстроте реализации (пригодится на олимпиадках) :)
Окей, вот вам тест для формы Н: нашу точку выносим «далеко-далеко». Тогда сумма площадей треугольников будет, очевидно, «очень-очень большой», а площадь самой буквы Н — сравнительно маленькой.
Возможно, вы имели ввиду ориентированную площадь? В таком случае да, он не всегда сработает вообще. Но для абсолютных (неотрицательных) площадей такой алгоритм, кажется, должен работать.
И еще: плюс такого подхода не только в быстроте работы, а и в быстроте реализации (пригодится на олимпиадках) :)
Вы правы. Но вот Вам еще одна идея: а что будет, если действительно таки использовать ориентированную площадь в вычислениях? Если я не ошибаюсь, то в Н-подобном случае и точки внутри сумма ориентированных площадей треугольников как раз будет равна ориентированной площади всего полигона. Но что и как будет происходить для точки за пределами, пока остается вопросом. Впрочем, это пока только догадки, и будет здорово, если у Вас есть ответ.
Ориентированная площадь из любой точки плоскости даст ±S многоугольника (в зависимости от направления обхода рёбер).
Более того, как считать площадь многоугольника, кроме как способом модуля от ориентинованной площади? :-D
Ориентированная площадь для меня наиболее простой и очевидный способ при наличии координат вершин многоугольника.
Более того, как считать площадь многоугольника, кроме как способом модуля от ориентинованной площади? :-D
Ориентированная площадь для меня наиболее простой и очевидный способ при наличии координат вершин многоугольника.
Да, надо сделать бесконечный луч в любую сторону из точки. Если количество пересечений нечётное, то точка внутри.
Если луч совпал с отрезком фигуры, тогда алгоритму задница.
Если луч совпал с отрезком фигуры, тогда алгоритму задница.
Я, может быть, немного троллю, но этот метод не работает, например, для множества бесконечно вложенных друг в друга плоских торов с радиусом от 0 до 1 :)
Принадлежность точки к выпуклой фигуре можно определить проще — точка должна находится по одну и туже сторону от каждого отрезка этой фигуры. В Вашем примере точка находится справа от каждого отрезка фигуры если смотреть обход фигуры по часовой стрелке.
Принадлежность к одной и той же стороне от отрезка легко посчитать через векторные произведения. Если все векторные произведения отрезков и вектора на исследуемую точку имеют один и тот же знак (положительны или отрицательны) то точка принадлежит фигуре, если они разные, то не принадлежит.
Тут всё элементарно просто, но если кому то нужно могу описать подробнее.
Принадлежность к одной и той же стороне от отрезка легко посчитать через векторные произведения. Если все векторные произведения отрезков и вектора на исследуемую точку имеют один и тот же знак (положительны или отрицательны) то точка принадлежит фигуре, если они разные, то не принадлежит.
Тут всё элементарно просто, но если кому то нужно могу описать подробнее.
xpro.ws/h.png
Тут лежит картинка, опровергающая ваш метод. Красным помечены отрезки, для которых точка лежит по другую сторону, в отличие от зеленых.
Тут лежит картинка, опровергающая ваш метод. Красным помечены отрезки, для которых точка лежит по другую сторону, в отличие от зеленых.
Этот алгоритм не правильный — если исходная точка лежит на продолжении какой-нибудь стороны многоугольника, то произойдет деление на ноль с непредсказуемым результатом.
Правильно брать atan2(y_{i+1},x_{i+1})-atan2(y_i,x_i) и нормировать до (-\pi;\pi] (если результат близок к \pm\pi, то точка лежит на стороне многоугольника). Еще нужно учесть совпадение какой-либо вершины многоугольника с нулем, если это допускается.
Правильно брать atan2(y_{i+1},x_{i+1})-atan2(y_i,x_i) и нормировать до (-\pi;\pi] (если результат близок к \pm\pi, то точка лежит на стороне многоугольника). Еще нужно учесть совпадение какой-либо вершины многоугольника с нулем, если это допускается.
Мне тоже попалась эта задача на олимпиаде. Тоже имел дело с турбо паскалем. Решил так:
В режиме graph рисуем зеленый треугольник, ставим красную точку. Далее заливаем треугольник белым. Проверяем цвета соседних с точкой пикселей. Если черные, значит точка не входит. Да, есть нюансы и вообще это мега читерство, но на олимпиаде главное чтобы программа правильно отрабатывала, а как никого не волнует.
В режиме graph рисуем зеленый треугольник, ставим красную точку. Далее заливаем треугольник белым. Проверяем цвета соседних с точкой пикселей. Если черные, значит точка не входит. Да, есть нюансы и вообще это мега читерство, но на олимпиаде главное чтобы программа правильно отрабатывала, а как никого не волнует.
берем полигон из 1000 точек
для каждой грани находим ее MBR и записываем в некий двумерный массив NxM(100х100?) флаги присутствия граней в какой либо ячейке.
Далее имеем точку в X,Y или в nX,mY в пространстве наложенной на полигон сетке.
достаточно пустить луч в минимальную сторону( влево\право\верх\низ ) и проверить попадание через обычный алгоритм пересечения отрезка чтобы получить профит.
Время создания изначальной структуры данных по присутствию граней aka двумерный массив ~ в 10 раз дольше чем одиночная проверка.
Итоговый тест вхождения, при наличии структуры, работает примерно в ~NxM раз быстрее чем одиночная проверка
для каждой грани находим ее MBR и записываем в некий двумерный массив NxM(100х100?) флаги присутствия граней в какой либо ячейке.
Далее имеем точку в X,Y или в nX,mY в пространстве наложенной на полигон сетке.
достаточно пустить луч в минимальную сторону( влево\право\верх\низ ) и проверить попадание через обычный алгоритм пересечения отрезка чтобы получить профит.
Время создания изначальной структуры данных по присутствию граней aka двумерный массив ~ в 10 раз дольше чем одиночная проверка.
Итоговый тест вхождения, при наличии структуры, работает примерно в ~NxM раз быстрее чем одиночная проверка
Вообще, для принадлежности точки полигону используют обычно метод подсчета числа пересечений. На каждой итерации данного метода выполняется: 2 сложения, 4 вычитания, 1 умножение, 1 деление и одна операция взятия знака числа.
В вашем алгоритме на каждую итерацию выполняется: 4 сложения, 2 вычитания, 8 умножений, 2 деления и 2 арктангенса. Где профит?
В вашем алгоритме на каждую итерацию выполняется: 4 сложения, 2 вычитания, 8 умножений, 2 деления и 2 арктангенса. Где профит?
Профита нет. Я не в коем разе не претендовал на написание самого крутого и быстрого алгоритма, упаси господи. В статьей хотел лишь показать ход своих мыслей (уточню — был 96 год и до создании Википедии было так лет 5 :) ). Спасибо за статью на Вики — там есть интересная ссылка на pdf-ку. И вот в этой самой стать, начало всех мат. выкладок очень похоже на мои потуги, что не может меня, конечно же, не радовать. Ну на следующие шаги моего серого вещества уже не хватило.
Я делал так: считал сумму углов из точки до концов отрезка, и так для каждого отрезка ломаной. Сам, блин, кустарно изобретал.
Результат был простой:
• если сумма равна ±2π, то точка внутри.
• если сумма равна 0, то точка снаружи.
• побочно: если сумма равна +-π, то точка на границе (с оговорками на точность арифметики).
Дырка была в том случае, если концы незамкнутой ломаной лежат на луче, исходящем из точки.
Но по условиям на входе был таки замкнутый многоугольник. ;-)
Позже проконсультировался с математиком, он предложил в общем случае интеграл по контуру (забыл какой функции), а в частном случае с ломаной таки сумму видимым углов обозрения, так как «изобрёл» я.
Результат был простой:
• если сумма равна ±2π, то точка внутри.
• если сумма равна 0, то точка снаружи.
• побочно: если сумма равна +-π, то точка на границе (с оговорками на точность арифметики).
Дырка была в том случае, если концы незамкнутой ломаной лежат на луче, исходящем из точки.
Но по условиям на входе был таки замкнутый многоугольник. ;-)
Позже проконсультировался с математиком, он предложил в общем случае интеграл по контуру (забыл какой функции), а в частном случае с ломаной таки сумму видимым углов обозрения, так как «изобрёл» я.
он работает для любых многоугольников, как выпуклых, так и невыпуклых.
исключения, я назвал, незамкнутые ломаные и точка на ребре (приходится доверять значению п+-epsilon).
угол вспомню чуть позже — с компа вместо мобилки.
но, вероятно вы правы: скорее через арккосинус скалярного.
тогда вычисления самозащищены от деления на ноль.
исключения, я назвал, незамкнутые ломаные и точка на ребре (приходится доверять значению п+-epsilon).
угол вспомню чуть позже — с компа вместо мобилки.
но, вероятно вы правы: скорее через арккосинус скалярного.
тогда вычисления самозащищены от деления на ноль.
Так-с… Я прикинул три фрагмента (на псевдокоде)
Фрагмент 1, через арксинус векторного произведения:
//=============================================================
//sin(a, b) = len(vector_prod(a, b)) / (len(a) * len(b))
float P0x, P0y; // origin of the angle
float P1x, P1y; // start of an angle segment
float P2x, P2y; // finish of an angle segment
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float vector_prod_x = Ay * 0.0 — 0.0 * By; // Bz and Az are zero
float vector_prod_y = 0.0 * Bx — Ax * 0.0; // Az and Bz are zero
float vector_prod_z = Ax * By — Ay * Bx;
float vector_prod_len = vector_prod_z; // singular case, no sqrt() needed
{//bug here!!!
if ( vector_prod_len == 0.0 )
throw Exception__Point_is_on_Segment;
float sin_gamma = vector_prod_len / (len_a * len_b);
};//bugged block finished
float gamma = asin(sin_gamma);
return gamma;
// total:
// arcsine: 1
// square root: 2
// multiplication: 11
// division: 1
// addition: 2
// substraction: 7
// test condition: 2
// conjunction: 2
// equality: 4
Фрагмент 2, через арккосинус скалярного произведения:
//cos(a, b) = scalar_prod(a, b) / (len(a) * len(b))
float P0x, P0y; // origin of the angle
float P1x, P1y; // start of an angle segment
float P2x, P2y; // finish of an angle segment
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float scalar_prod = Ax * Bx + Ay * By;
float cos_gamma = cos_gamma = scalar_prod / (len_a * len_b);
float gamma = acos(cos_gamma);
return gamma;
// total:
// arccosine: 1
// square root: 2
// multiplication: 7
// division: 1
// addition: 3
// substraction: 4
// test condition: 2
// conjunction: 2
// equality: 4
Фрагмент 3, через площадь треугольника детерминантом и площадь синусом:
//=============================================================
// surface of a triangulum is equal to a half
// of the coordinated matrix determinant:
// |Ox, Oy, 1|
// S = (1/2) * |Ax, Ay, 1|
// |Bx, By, 1|
// S = (1/2) * (Ox * (Ay — By) + Ax * (By — Oy) + Bx * (Oy — Ay) =
// (considering Ox, Oy are zero)
// = Ax * By – Bx * Ay
//
// also
// surface of triangulum is
// S = (1/2) * |OA| * |OB| * sin_gamma
//
// therefore
// sin_gamma = 2 * S / (|OA| * |OB|) = determinant / (|OA| * |OB|)
float x0, y0; // point to test, point_0
float x1, y1; // segment start, point_1
float x2, y2; // segment finish, point_2
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float determinant = Ax * By — Bx * Ay;
float sin_gamma;
// if the triangle is degenerate, determinant is zero, angle is zero,
// and point is on the segment
{//bug here!!!
if ( determinant == 0.0 )
throw Exception__Point_is_on_Segment;
float sin_gamma = determinant / (len_a * len_b);
};//bugged block finished
float gamma = asin(sin_gamma);
return gamma;
// total:
// arcsine: 1
// square root: 2
// multiplication: 6
// division: 1
// addition: 2
// substraction: 5
// test condition: 3
// conjunction: 2
// equality: 5
Первый фрагмент глюкавый (помечено).
Второй фрагмент на одно умножение сложнее третьего и
Третий фрагмент получается самым оптимальным, но опять глюк на синусе…
Ну, так и получается, что через арккосинус скалярного проще и вернее.
Кстати, если точка внутри фигуры, то я насчитал два случая +2π и -2π.
И если точка на ребре, то тоже вижу два случая π и 3π.
А так вообще везде надо перепроверить операцию «== 0.0» на корректность. Мало ли…
Фрагмент 1, через арксинус векторного произведения:
//=============================================================
//sin(a, b) = len(vector_prod(a, b)) / (len(a) * len(b))
float P0x, P0y; // origin of the angle
float P1x, P1y; // start of an angle segment
float P2x, P2y; // finish of an angle segment
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float vector_prod_x = Ay * 0.0 — 0.0 * By; // Bz and Az are zero
float vector_prod_y = 0.0 * Bx — Ax * 0.0; // Az and Bz are zero
float vector_prod_z = Ax * By — Ay * Bx;
float vector_prod_len = vector_prod_z; // singular case, no sqrt() needed
{//bug here!!!
if ( vector_prod_len == 0.0 )
throw Exception__Point_is_on_Segment;
float sin_gamma = vector_prod_len / (len_a * len_b);
};//bugged block finished
float gamma = asin(sin_gamma);
return gamma;
// total:
// arcsine: 1
// square root: 2
// multiplication: 11
// division: 1
// addition: 2
// substraction: 7
// test condition: 2
// conjunction: 2
// equality: 4
Фрагмент 2, через арккосинус скалярного произведения:
//cos(a, b) = scalar_prod(a, b) / (len(a) * len(b))
float P0x, P0y; // origin of the angle
float P1x, P1y; // start of an angle segment
float P2x, P2y; // finish of an angle segment
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float scalar_prod = Ax * Bx + Ay * By;
float cos_gamma = cos_gamma = scalar_prod / (len_a * len_b);
float gamma = acos(cos_gamma);
return gamma;
// total:
// arccosine: 1
// square root: 2
// multiplication: 7
// division: 1
// addition: 3
// substraction: 4
// test condition: 2
// conjunction: 2
// equality: 4
Фрагмент 3, через площадь треугольника детерминантом и площадь синусом:
//=============================================================
// surface of a triangulum is equal to a half
// of the coordinated matrix determinant:
// |Ox, Oy, 1|
// S = (1/2) * |Ax, Ay, 1|
// |Bx, By, 1|
// S = (1/2) * (Ox * (Ay — By) + Ax * (By — Oy) + Bx * (Oy — Ay) =
// (considering Ox, Oy are zero)
// = Ax * By – Bx * Ay
//
// also
// surface of triangulum is
// S = (1/2) * |OA| * |OB| * sin_gamma
//
// therefore
// sin_gamma = 2 * S / (|OA| * |OB|) = determinant / (|OA| * |OB|)
float x0, y0; // point to test, point_0
float x1, y1; // segment start, point_1
float x2, y2; // segment finish, point_2
float Ax = P1x — P0x, Ay = P1y — P0y; // convert segment (P0,P1) to (0,A)
float Bx = P2x — P0x, By = P2y — P0y; // convert segment (P0,P2) to (0,B)
if ( Ax == 0.0 && Ay == 0.0 ) // len_a == 0.0
throw Exception__Point_is_on_Vertex;
if ( Bx == 0.0 && By == 0.0 ) // len_b == 0.0
throw Exception__Point_is_on_Vertex;
float len_a = sqrt(Ax * Ax + Ay * Ay); // length of vector a
float len_b = sqrt(Bx * Bx + By * By); // length of vector b
float determinant = Ax * By — Bx * Ay;
float sin_gamma;
// if the triangle is degenerate, determinant is zero, angle is zero,
// and point is on the segment
{//bug here!!!
if ( determinant == 0.0 )
throw Exception__Point_is_on_Segment;
float sin_gamma = determinant / (len_a * len_b);
};//bugged block finished
float gamma = asin(sin_gamma);
return gamma;
// total:
// arcsine: 1
// square root: 2
// multiplication: 6
// division: 1
// addition: 2
// substraction: 5
// test condition: 3
// conjunction: 2
// equality: 5
Первый фрагмент глюкавый (помечено).
Второй фрагмент на одно умножение сложнее третьего и
Третий фрагмент получается самым оптимальным, но опять глюк на синусе…
Ну, так и получается, что через арккосинус скалярного проще и вернее.
Кстати, если точка внутри фигуры, то я насчитал два случая +2π и -2π.
И если точка на ребре, то тоже вижу два случая π и 3π.
А так вообще везде надо перепроверить операцию «== 0.0» на корректность. Мало ли…
Классический способ — создание горизонтального отрезка от точки до точки гарантированно лежащей вне контура, обычно очень далеко влево. После чего считаем число пересечений отрезка с гранями полигона.
Если число чётное — мы вне полигона, иначе — внутри.
Если число чётное — мы вне полигона, иначе — внутри.
Простите, не удержался.
Что Вы называете математическими задачами? Встречаются задачи, в которых требуется вывести одну формулу математическими методами и тупо считать для нее аргументы, но таких задач — одна из ста. Если Вас беспокоит, что многие алгоритмы и идеи имеют под собой немаленькую математическую базу, то тут тоже нечему удивляться, ведь теория алгоритмов — раздел математики. А на смекалку задачи бывают и на интуицию бывают и реализационные, в которых надо написать 800 строк кода просто сделав, что требуется.
Sign up to leave a comment.
Алгоритм определения попадания точки в контур на основе комплексного анализа