Comments 21
Моё почтение, получилось гораздо красивее традиционной кардиоиды, которую обычно в таких случаях используют
Вы молодец :)
П.С. хотел Вам плюсик в карму поставить но обнаружил что уже за что-то поставил )))
Вы молодец :)
П.С. хотел Вам плюсик в карму поставить но обнаружил что уже за что-то поставил )))
Вы ещё про математическое порно вспомните.
Вот посвежее:
www.google.com/search?hl=uk&safe=off&tbo=d&output=search&sclient=psy-ab&q=exp%28%28-%28%28%28x-4%29^2%2B%28y-4%29^2%29^2%29%29%2F1000%29%2Bexp%28%28-%28%28%28x%2B4%29^2%2B%28y%2B4%29^2%29^2%29%29%2F1000%29%2B0.15*exp%28-%28%28%28x%2B4%29^2%2B%28y%2B4%29^2%29^2%29%29%2B0.15*exp%28-%28%28%28x-4%29^2%2B%28y-4%29^2%29^2%29%29&btnK
Функция:
exp((-(((x-4)^2+(y-4)^2)^2))/1000)+exp((-(((x+4)^2+(y+4)^2)^2))/1000)+0.15*exp(-(((x+4)^2+(y+ 4)^2)^2))+0.15*exp(-(((x-4)^2+(y-4)^2)^2
www.google.com/search?hl=uk&safe=off&tbo=d&output=search&sclient=psy-ab&q=exp%28%28-%28%28%28x-4%29^2%2B%28y-4%29^2%29^2%29%29%2F1000%29%2Bexp%28%28-%28%28%28x%2B4%29^2%2B%28y%2B4%29^2%29^2%29%29%2F1000%29%2B0.15*exp%28-%28%28%28x%2B4%29^2%2B%28y%2B4%29^2%29^2%29%29%2B0.15*exp%28-%28%28%28x-4%29^2%2B%28y-4%29^2%29^2%29%29&btnK
Функция:
exp((-(((x-4)^2+(y-4)^2)^2))/1000)+exp((-(((x+4)^2+(y+4)^2)^2))/1000)+0.15*exp(-(((x+4)^2+(y+ 4)^2)^2))+0.15*exp(-(((x-4)^2+(y-4)^2)^2
я один не знал, что гугль способен выдавать графики таких функций, да ещё и в HTML5? O_O
(в один клик: vk.cc/1gRXOa)
(в один клик: vk.cc/1gRXOa)
Opa Gangnam Style www.wolframalpha.com/input/?i=PSY+curve
Пытаюсь обоину написать на андроид, да вот беда: толь я дурак, толь не я… Но пока не особо получается по этой формуле:
Буду использовать формулы от товарищей повыше.
Screenshot
Буду использовать формулы от товарищей повыше.
Используйте. А что конкретно вы сделали, чтобы получить эту кеглю?
Вообще: пробегаю по всей дуге 360° c шагом в 1°, координаты точки расчитываются вот примерно так:
(кстати, забыл упомянуть, что ось y пришлось инвертировать)
Я идиот. Забыл, что Math класс работает в радианах. Все нормально.
(кстати, забыл упомянуть, что ось y пришлось инвертировать)
private void heartPoint(float angle) {
point[0] = (float) Math.cos(angle);
point[1] = (float) -(Math.sin(angle) + Math.sqrt(Math.abs(point[0])));
}
Я идиот. Забыл, что Math класс работает в радианах. Все нормально.
Вот как можно получить сердце на WolframAlpha. Можно скопировать ссылку и послать в виде открытки или там скачать рисунок :)
Да, интересный факт: площадь моего «сердечка» равняется площади исходной окружности (т.е. π*(d/2)2, где d — длина отрезка, по которому сердечко пересекается с осью ординат).
>… и представим, что она состоит из желе, будучи при этом жёстко прикреплена к оси ординат. Теперь «подуем» на неё снизу…
Очень хорошо, что вы это понимаете, такого чувства «графика» многим не хватает.
Очень хорошо, что вы это понимаете, такого чувства «графика» многим не хватает.
Эх, помнится, несколько лет назад пытался сообразить такую функцию, вейвлет-образ которой получился бы в форме сердечка. Не слишком удачно вышло, а потом подбирать надоело.
5 лет назад на курсе по матлабу делал похожее. Только у меня получилось хуже.
Вспомнилась 3D Роза методом Монте-Карло в один килобайт.
Sign up to leave a comment.
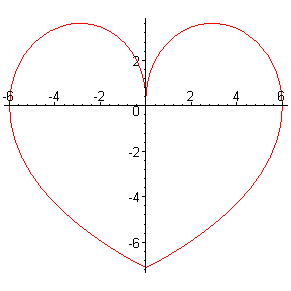
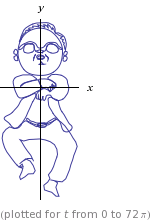
Пусть математика сложит сердца