Язык 4DL был изобретён в 2001 г. автором Cliff L. Biffle. Как он сам объяснил, придумал он его во-первых, потому, что до этого языков с четырехмерными программами не существовало, а во-вторых, потому что четырёхмерное пространство довольно сложно для понимания, и надо же дать людям возможность потренировать мозги.
Русская Википедия относит этот язык к семейству «фунгеоидных». Это языки, ведущие свой род от языка Befunge, программы в котором записываются в виде символов на прямоугольной решётке и могут выполняться в произвольном направлении. В 4DL для представления программы используется четырёхмерная решётка, и направлений её выполнения, соответственно, 8.
Программа на 4DL может выглядеть, например, вот так:
Эта программа написана не на «базовом» языке, а на его расширении, но об этом позже.
Кроме того, что язык 4DL фунгеоидный, он ещё и стековый. Единственным объектом данных, с которым может работать программа, является стек целых чисел. В него кладутся числа, вводимые символы, и из него берутся символы для печати.
Вот как выглядит система команд, предложенная автором:
В качестве примера программы автор приводит «Hello, World!» (по меньшей мере, с тремя ошибками). К сожалению, ни на что заметно более серьёзное язык с такими командами не способен (если не увеличивать размер программы во много раз), поэтому, для начала я решил добавить к нему еще парочку команд:
Жизнь стала гораздо веселее. Например, вот как выглядит программа, печатающая сумму чисел из входной строки:
Несколько слов о записи программы (это уже мои фантазии — автор никак не описывал входной синтаксис).
Пространство, в котором находится программа, делится на двумерные слои, в которых координаты Z и T постоянны. Символы каждого слоя записываются в виде прямоугольной таблицы, начиная с угла X=Y=0. Если это символ из ASCII-7 (с кодом от 33 до 126), он пишется явно. Если нет — записывается его двузначный 16-ричный код. Пробел можно обозначать как 20 или как двойное подчёркивание. Символы пишутся через любое число пробелов, строчка с ними начинается с пробела.
Прямоугольники объединяются в двумерную таблицу. По горизонтали идут слои с одинаковым значением T (последовательно: Z=0, Z=1, ...), по вертикали — столбцы с одинаковым значением Z. Длины строчек в слоях, число строчек в слое, число слоёв в строке таблицы могут различаться — недостающие клетки будут заполнены символами с кодом 0. Слои в строке таблицы разделяются символами || а сами строки — строчками, начинающимися с минуса.
По умолчанию выполнение начинается с ячейки (0,0,0,0) в направлении X+. Стартовую точку можно переопределить, вставив в программу строку >x,y,z,t (числа x,y,z и t десятичные).
Траектория выполнения приведённой выше программы в 4-мерном пространстве выглядит примерно так:
Кроме ячеек, через которые проходит красная линия, есть ещё некоторое количество ячеек с данными, но их я решил не показывать.
Довольно быстро оказывается понятно, что мощность языка 4DL целиком определяется мощностью лежащей в его основе стековой машинки. Так, если разрядность числа, лежащего в стеке, ограничена, то можно реализовать те и только те алгоритмы, которые реализуются на конечных автоматах со стековой памятью. Если в стеке разрешено размещать сколь угодно длинные числа, и у нас есть операция обмена двух ячеек в вершине стека, язык становится Тьюринг-полным — но реализация машины Тьюринга на нём была бы чересчур медленной (одна операция выполнялась бы не меньше 2^2^N шагов, где N — размер используемой памяти). Если размер числа в стеке ограничен, но есть операция чтения и модификации ячеек в глубине стека (смещение от вершины берётся также из стека), то получим почти ТП-язык — доступная память прямого доступа будет ограничена.
В любом случае, четырёхмерность программы почти не используется, и любую программу на 4DL можно вложить в двумерное пространство. Причём строку Y=0 оставить для исполняемого кода, Y=1 — для данных, а остальную часть плоскости использовать для реализации команд перехода. Этот вариант кажется неинтересным.
Авторы языка Befunge наткнулись у себя на ту же проблему ограничения мощности. Для её решения они добавили в язык механизм модификации ячеек памяти (что правильно), но сделали это, разрешив обращаться к ячейкам — как для чтения, так и для записи — по явным координатам. Мне это показалось слишком сильным решением.
Более умеренный вариант предложен автором одной из реализаций языка 4DL — Bernhard Stoeckner. В «расширенной» системе команд своей реализации он предлагает, помимо прочего, такие команды:
Оказывается, что этих команд достаточно, чтобы сделать язык Тьюринг-полным даже при 8-битной ячейке стека (не говоря уже о 32-битной). Чтобы доказать это, пойдём по самому простому пути — реализуем машину Тьюринга :)
Основная проблема у нас в том, что мы можем читать и менять содержимое только ячеек памяти, соседних с текущей точкой выполнения программы. Для машины Тюринга нужна бесконечная, или хотя бы полубесконечная лента, а значит, для общения с далёкими ячейками программа должна быть самомодифицирующейся.
Первой идеей было реализовать ленту в виде «небоскрёба», в котором каждый этаж мог поддерживать команды «прочитать ячейку ленты», «изменить содержимое ячейки», «сдвинуться вверх» и «сдвинуться вниз», а когда дойдёт до самого верха — запустить «строительную площадку», которая растёт в параллельном слое реальности, для строительства нового этажа. Задача оказалась разрешимой, но довольно быстро удалось обнаружить гораздо более простой путь.
Оказывается, если взять строчку программы, например, в направлении X+, левую её часть заполнить пробелами, а где-то поместить команду «N» (взять символ из стека и записать его в ячейку справа), потом положить в стек определённые последовательности команд и данных, и отправить программу выполнять эту строчку, то программа может сделать то, что вам необходимо, и вернуться обратно.
Например, последовательность [N,x,x,N] превратит строчку
в строчку
А если после этого отправить в эту строчку последовательность [n,n,n,N,n], то получится строка
— самая левая команда «N» сдвинется на ячейку левее. Аналогично, в два приёма можно выполнить команды «сдвинуться вправо», «записать символ в соседнюю строчку» и «прочитать символ из соседней строчки». Удобнее всего работать с ячейкой, находящейся на две позиции правее ячейки, в которой находится команда «N».
Программа, реализующая машину Тьюринга, будет состоять из трёх частей. Слой T=0 будем использовать для коммуникации между программой и лентой. Программа будет находиться в области T>0, Z=0 и представлять собой конечный автомат (с памятью), преобразующий текущий символ на ленте в пару (новый символ, направление сдвига). Ленту поместим на прямую Y=Z=T=1, а программа управления будет занимать область T>0, Z=1. Интерфейс ленты дополняет интерфейс программы: по паре (символ, направление сдвига) она меняет содержимое ленты, сдвигает каретку, и возвращает новый символ, на который указывает каретка.
Назначение слоя коммуникации — передача управления от программы к ленте и обратно, а также отладочная печать. Кроме того, этот слой выполняет старт программы (издержки реализации: для начала выполнения надо явно положить в стек содержимое ячейки, на которую указывает каретка).
Текущее состояние программы хранится с помощью модификации кода. Для выполнения обработки управление передаётся в точку (2,3,0,1) в направлении T+, и идёт по прямой, заполненной командами «T» за исключением одной клетки, соответствующей текущему состоянию. В этой клетке находится команда «x» (пойти влево). Программа «выходит на нужном этаже», меняет команду «x» на «T», потом анализирует символ в вершине стека, кладёт в стек желаемые направление движения и новый символ, после чего боковыми дорожками добирается до «этажа», соответствующего новому состоянию, там кладёт в ячейку (2,3,0,T) команду «x» и уходит на плоскость Z=T=0, где её переправляют на управление лентой.
Собственно, всё. Вот пример программы, реализующей удвоение числа, записанного на ленте. В программе 7 состояний, на ленте сейчас число 2 (две единицы).
Если эту программу запустить, она напечатает
Каждая тройка символов — это новый символ, который нужно оставить на ленте (0 или 1), направление, куда сдвинуться (0 — на месте, 1 — влево, 2 — вправо) и символ, который оказался под новым положением каретки. Можно проверить, что программа всё сделала правильно, и получилось число 4.
С некоторыми усилиями, эту реализацию тоже можно уместить в 2D. Но в 4 измерениях работать несколько приятнее — гораздо больше свободы.
Можно слегка расширить язык — добавить команды умножения, деления с остатком, и занесения на стек числа 256 (для более удобного разделения числа на байты для записи в память). Правда, возникнут проблемы с отрицательными числами. Можно вместо 256 добавить команды «отщепить младший байт» ([x] => [x&0xff,x>>8]) и «приклеить младший байт» ([x,y] => [x+(y<<8)]). Но это только сделает язык удобнее, не изменив его сути. Интереснее посмотреть, что в языке лишнее, и как лучше использовать многомерную память.
Например:
Кстати, на esolang обнаружилась ещё парочка четырёхмерных (точнее, многомерных) языков. Оба — диалекты BrainFuck. Но в одном каретка блуждает по многомерной памяти, а программа выглядит, как строчка на BF, а в другом наоборот — программа многомерна, зато память линейна. Отличие от 4DL — что в обоих случаях управление и работа с памятью разделены.
Страничка 4DL на esolang
Страничка из блога автора
Сайт с интерпретатором
Befunge и его диалекты
Brainfuck с многомерной памятью
Brainfuck с многомерной программой
Русская Википедия относит этот язык к семейству «фунгеоидных». Это языки, ведущие свой род от языка Befunge, программы в котором записываются в виде символов на прямоугольной решётке и могут выполняться в произвольном направлении. В 4DL для представления программы используется четырёхмерная решётка, и направлений её выполнения, соответственно, 8.
Программа на 4DL может выглядеть, например, вот так:
X , B / \ B + 2 B - < ? T B - T
y __ 10 __ __ 7 __ __ A __ __ __ __ 07 __ __
------------------------------------------------------------------
__ Y __ __ __ __ __ __ __ __ . __ x __ __ x || __ __ __ __ __ __ __ __ __ __ 20 __ __ __ __ __
t X __ __ __ q + 2 q - < ? Z q - Z || z __ __ __ __ __ __ __ __ . b . x __ __ x
Эта программа написана не на «базовом» языке, а на его расширении, но об этом позже.
Кроме того, что язык 4DL фунгеоидный, он ещё и стековый. Единственным объектом данных, с которым может работать программа, является стек целых чисел. В него кладутся числа, вводимые символы, и из него берутся символы для печати.
Программы на 4DL
Вот как выглядит система команд, предложенная автором:
| X | Повернуть указатель на команду в направлении X+ |
| x | Повернуть указатель на команду в направлении X- |
| Y | Повернуть указатель на команду в направлении Y+ |
| y | Повернуть указатель на команду в направлении Y- |
| Z | Повернуть указатель на команду в направлении Z+ |
| z | Повернуть указатель на команду в направлении Z- |
| T | Повернуть указатель на команду в направлении T+ |
| t | Повернуть указатель на команду в направлении T- |
| P | Положить на стек символ из соседней клетки со стороны X+ |
| p | Положить на стек символ из соседней клетки со стороны X- |
| B | Положить на стек символ из соседней клетки со стороны Y+ |
| b | Положить на стек символ из соседней клетки со стороны Y- |
| D | Положить на стек символ из соседней клетки со стороны Z+ |
| d | Положить на стек символ из соседней клетки со стороны Z- |
| Q | Положить на стек символ из соседней клетки со стороны T+ |
| q | Положить на стек символ из соседней клетки со стороны T- |
| + | Взять сумму двух чисел на вершине стека, положить результат на стек |
| — | Взять разность двух чисел на вершине стека, положить результат на стек |
| , | Ввести символ с клавиатуры и положить его на стек |
| . | Снять символ с вершины стека и вывести на экран |
| # | Перепрыгнуть через следующую клетку программы |
| ? | Снять число с вершины стека, и если оно ненулевое, то перепрыгнуть через следующую клетку программы |
| 0 | Положить на стек число 0 |
| 2 | Положить на стек копию числа на его вершине |
| % | Закончить выполнение программы |
В качестве примера программы автор приводит «Hello, World!» (по меньшей мере, с тремя ошибками). К сожалению, ни на что заметно более серьёзное язык с такими командами не способен (если не увеличивать размер программы во много раз), поэтому, для начала я решил добавить к нему еще парочку команд:
| \ | Поменять содержимое двух ячеек на вершине стека |
| ^ | Снять число с вершины стека и ничего с ним не делать (эквивалентно 2-+ или ?XX — в случае движения вправо) |
Жизнь стала гораздо веселее. Например, вот как выглядит программа, печатающая сумму чисел из входной строки:
0 X , D - 2 ? T D - 2 ? T D - Y || __ z __ 0D __ __ __ __ 13 __ __ __ __ 10
__ __ Y D T ? 2 - D T ? 2 - D , x || __ __ __ 10 __ __ __ __ 13 __ __ __ __ 0D
__ __ X - \ 2 2 + 2 + + 2 + + __ y
-------------------
T t __ __ __ __ __ ^ __ __ __ __ x || __ t
+ y + ^ x __ __ __ __ ^ || __ y __ __ . B . B x
D || 01 __ __ __ __ 0A __ 0D
y \ + x
__ X __ y
-------------------
Y 0 x \ 0 ^ , x + x || __ __ __ __ __ Y __ __ . x
\ __ y Z ? 2 \ - x y || __ __ __ X + X 2 ? t y
D __ __ __ X + D \ y || 0A __ __ __ __ __ 3A
X \ 2 ? y D - Y || __ __ __ __ __ 01
y t ? 2 - D \ x || __ __ __ __ __ 01
Несколько слов о записи программы (это уже мои фантазии — автор никак не описывал входной синтаксис).
Пространство, в котором находится программа, делится на двумерные слои, в которых координаты Z и T постоянны. Символы каждого слоя записываются в виде прямоугольной таблицы, начиная с угла X=Y=0. Если это символ из ASCII-7 (с кодом от 33 до 126), он пишется явно. Если нет — записывается его двузначный 16-ричный код. Пробел можно обозначать как 20 или как двойное подчёркивание. Символы пишутся через любое число пробелов, строчка с ними начинается с пробела.
Прямоугольники объединяются в двумерную таблицу. По горизонтали идут слои с одинаковым значением T (последовательно: Z=0, Z=1, ...), по вертикали — столбцы с одинаковым значением Z. Длины строчек в слоях, число строчек в слое, число слоёв в строке таблицы могут различаться — недостающие клетки будут заполнены символами с кодом 0. Слои в строке таблицы разделяются символами || а сами строки — строчками, начинающимися с минуса.
По умолчанию выполнение начинается с ячейки (0,0,0,0) в направлении X+. Стартовую точку можно переопределить, вставив в программу строку >x,y,z,t (числа x,y,z и t десятичные).
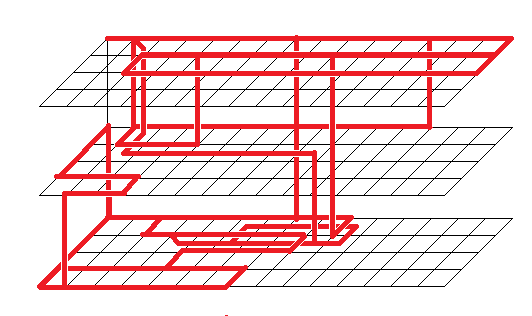
Траектория выполнения приведённой выше программы в 4-мерном пространстве выглядит примерно так:

Кроме ячеек, через которые проходит красная линия, есть ещё некоторое количество ячеек с данными, но их я решил не показывать.
Тьюринг-полный или нет?
Довольно быстро оказывается понятно, что мощность языка 4DL целиком определяется мощностью лежащей в его основе стековой машинки. Так, если разрядность числа, лежащего в стеке, ограничена, то можно реализовать те и только те алгоритмы, которые реализуются на конечных автоматах со стековой памятью. Если в стеке разрешено размещать сколь угодно длинные числа, и у нас есть операция обмена двух ячеек в вершине стека, язык становится Тьюринг-полным — но реализация машины Тьюринга на нём была бы чересчур медленной (одна операция выполнялась бы не меньше 2^2^N шагов, где N — размер используемой памяти). Если размер числа в стеке ограничен, но есть операция чтения и модификации ячеек в глубине стека (смещение от вершины берётся также из стека), то получим почти ТП-язык — доступная память прямого доступа будет ограничена.
В любом случае, четырёхмерность программы почти не используется, и любую программу на 4DL можно вложить в двумерное пространство. Причём строку Y=0 оставить для исполняемого кода, Y=1 — для данных, а остальную часть плоскости использовать для реализации команд перехода. Этот вариант кажется неинтересным.
Авторы языка Befunge наткнулись у себя на ту же проблему ограничения мощности. Для её решения они добавили в язык механизм модификации ячеек памяти (что правильно), но сделали это, разрешив обращаться к ячейкам — как для чтения, так и для записи — по явным координатам. Мне это показалось слишком сильным решением.
4DL+ и машина Тьюринга
Более умеренный вариант предложен автором одной из реализаций языка 4DL — Bernhard Stoeckner. В «расширенной» системе команд своей реализации он предлагает, помимо прочего, такие команды:
| N | Положить символ из стека в соседнюю клетку со стороны X+ |
| n | Положить символ из стека в соседнюю клетку со стороны X- |
| F | Положить символ из стека в соседнюю клетку со стороны Y+ |
| f | Положить символ из стека в соседнюю клетку со стороны Y- |
| G | Положить символ из стека в соседнюю клетку со стороны Z+ |
| g | Положить символ из стека в соседнюю клетку со стороны Z- |
| H | Положить символ из стека в соседнюю клетку со стороны T+ |
| h | Положить символ из стека в соседнюю клетку со стороны T- |
Оказывается, что этих команд достаточно, чтобы сделать язык Тьюринг-полным даже при 8-битной ячейке стека (не говоря уже о 32-битной). Чтобы доказать это, пойдём по самому простому пути — реализуем машину Тьюринга :)
Основная проблема у нас в том, что мы можем читать и менять содержимое только ячеек памяти, соседних с текущей точкой выполнения программы. Для машины Тюринга нужна бесконечная, или хотя бы полубесконечная лента, а значит, для общения с далёкими ячейками программа должна быть самомодифицирующейся.
Первой идеей было реализовать ленту в виде «небоскрёба», в котором каждый этаж мог поддерживать команды «прочитать ячейку ленты», «изменить содержимое ячейки», «сдвинуться вверх» и «сдвинуться вниз», а когда дойдёт до самого верха — запустить «строительную площадку», которая растёт в параллельном слое реальности, для строительства нового этажа. Задача оказалась разрешимой, но довольно быстро удалось обнаружить гораздо более простой путь.
Оказывается, если взять строчку программы, например, в направлении X+, левую её часть заполнить пробелами, а где-то поместить команду «N» (взять символ из стека и записать его в ячейку справа), потом положить в стек определённые последовательности команд и данных, и отправить программу выполнять эту строчку, то программа может сделать то, что вам необходимо, и вернуться обратно.
Например, последовательность [N,x,x,N] превратит строчку
__ __ __ __ N
в строчку
__ __ __ __ N N x
А если после этого отправить в эту строчку последовательность [n,n,n,N,n], то получится строка
__ __ __ N n n x
— самая левая команда «N» сдвинется на ячейку левее. Аналогично, в два приёма можно выполнить команды «сдвинуться вправо», «записать символ в соседнюю строчку» и «прочитать символ из соседней строчки». Удобнее всего работать с ячейкой, находящейся на две позиции правее ячейки, в которой находится команда «N».
Программа, реализующая машину Тьюринга, будет состоять из трёх частей. Слой T=0 будем использовать для коммуникации между программой и лентой. Программа будет находиться в области T>0, Z=0 и представлять собой конечный автомат (с памятью), преобразующий текущий символ на ленте в пару (новый символ, направление сдвига). Ленту поместим на прямую Y=Z=T=1, а программа управления будет занимать область T>0, Z=1. Интерфейс ленты дополняет интерфейс программы: по паре (символ, направление сдвига) она меняет содержимое ленты, сдвигает каретку, и возвращает новый символ, на который указывает каретка.
Назначение слоя коммуникации — передача управления от программы к ленте и обратно, а также отладочная печать. Кроме того, этот слой выполняет старт программы (издержки реализации: для начала выполнения надо явно положить в стек содержимое ячейки, на которую указывает каретка).
Текущее состояние программы хранится с помощью модификации кода. Для выполнения обработки управление передаётся в точку (2,3,0,1) в направлении T+, и идёт по прямой, заполненной командами «T» за исключением одной клетки, соответствующей текущему состоянию. В этой клетке находится команда «x» (пойти влево). Программа «выходит на нужном этаже», меняет команду «x» на «T», потом анализирует символ в вершине стека, кладёт в стек желаемые направление движения и новый символ, после чего боковыми дорожками добирается до «этажа», соответствующего новому состоянию, там кладёт в ячейку (2,3,0,T) команду «x» и уходит на плоскость Z=T=0, где её переправляют на управление лентой.
Собственно, всё. Вот пример программы, реализующей удвоение числа, записанного на ленте. В программе 7 состояний, на ленте сейчас число 2 (две единицы).
Программа
B __ Y || T X 2 Y
01 __ __ || __ __ __ P 0
__ __ __ || y \ . + b 2 x
__ __ T . B x || __ __ 0 X . z __
Z __ __ __ __ || X 2 b + . \ y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 01 __ __ __ __ || Y t X # ? __ # \ __ __ N __ __ __
__ T __ __ X b b __ __ __ Y || __ __ T __ __ __ __ __ __ __ FF 00 01 01 00
X b F ? y B B Y __ __ __ || N __ p
y __ x x __ 02 00 T __ Y T || __ __ y
t __ f b __ __ __ __ __ x __ || __ __ T
|| N __ p
|| __ __ y __ __ __ __ __ __ __ __ x
|| X Q Q Q Q Q Q Q Q Q Q y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 00 __ __ __ __ || __ __ t __ __ __ __ __ __ __ __ x
__ T __ __ X b b __ Y __ __ || __ __ X B B B B B B B B y
X b F ? y B B Y __ __ __ || __ __ __ 01 # # F x x N N
y __ T x __ 02 01 Y T __ __ || __ __ __
t __ f b __ __ __ x __ __ __ || __ __ 2
|| __ __ __
|| __ __ __
|| __ 00 01 # # B x x N 01 N
--------------------------------------------------------------------------------
__ __ __ __ __ 01 01 __ __ __ __ ||
__ T __ __ X b b Y __ __ __ ||
X b F ? y B B __ Y __ __ ||
y __ T x __ 02 01 T Y __ __ || __ __ __
t __ f b __ __ __ __ x __ __ || __ __ ?
--------------------------------------------------------------------------------
__ __ __ __ __ 01 00 __ __ __ __ ||
__ T __ __ X b b __ Y __ __ ||
X b F ? y B B Y __ __ __ ||
y __ T x __ 01 01 Y T __ __ || __ __ t __ x
t __ f b __ __ __ x __ __ __ || __ __ X ^ y
--------------------------------------------------------------------------------
__ __ __ __ __ 02 01 __ __ __ __ ||
__ T __ __ X b b __ __ Y __ ||
X b F ? y B B __ Y __ __ ||
y __ T x __ 01 01 __ Y t __ || __ __ __
t __ f b __ __ __ __ x __ __ || __ __ P 01
--------------------------------------------------------------------------------
__ __ __ __ __ 01 00 __ __ __ __ ||
__ T __ __ X b b Y __ __ __ ||
X b F ? y B B __ __ __ Y ||
y __ T x __ 02 01 T __ __ Y || __ __ __
t __ f b __ __ __ __ __ __ x || __ __ -
--------------------------------------------------------------------------------
__ __ __ __ __ __ __ __ __ __ __ ||
__ T __ __ % __ __ __ __ __ __ ||
X b F ? y B B Y __ __ __ ||
y __ T x __ 00 00 Y __ __ __ || __ __ __
t __ f b __ __ __ x __ __ __ || __ __ ?
--------------------------------------------------------------------------------
||
||
|| __ __ __ __ N 01 x x N
|| __ __ t __ b b b b b x
|| __ __ X B B B B B B y
|| __ __ __ n N n n 01 n
--------------------------------------------------------------------------------
||
||
|| __ __ __ __ N 01 N x x n
|| __ __ t __ b b b b b b x
|| __ __ X B B B B B B B y
|| __ __ __ N N N __ 01 n n
Если эту программу запустить, она напечатает
021 120 020 110 011 110 121 020 021 120 111 110 010 120 121 121 120 011 000
Каждая тройка символов — это новый символ, который нужно оставить на ленте (0 или 1), направление, куда сдвинуться (0 — на месте, 1 — влево, 2 — вправо) и символ, который оказался под новым положением каретки. Можно проверить, что программа всё сделала правильно, и получилось число 4.
С некоторыми усилиями, эту реализацию тоже можно уместить в 2D. Но в 4 измерениях работать несколько приятнее — гораздо больше свободы.
Что дальше?
Можно слегка расширить язык — добавить команды умножения, деления с остатком, и занесения на стек числа 256 (для более удобного разделения числа на байты для записи в память). Правда, возникнут проблемы с отрицательными числами. Можно вместо 256 добавить команды «отщепить младший байт» ([x] => [x&0xff,x>>8]) и «приклеить младший байт» ([x,y] => [x+(y<<8)]). Но это только сделает язык удобнее, не изменив его сути. Интереснее посмотреть, что в языке лишнее, и как лучше использовать многомерную память.
Например:
- можно ли убрать стек и оставить только 8- или 32-битный аккумулятор?
- а если после этого добавить fork (каждый процесс со своим аккумулятором)?
- а если вместо аккумуляторов реализовать параллельный слой данных, так, что в каждой ячейке будет одна команда и один байт данных?
- … и заставить все ячейки работать параллельно и одновременно каждый такт?
- Это уже получились схемы из Майнкрафта, или пока ещё нет?
А если нет, тогда я выпью ещё...
Кстати, на esolang обнаружилась ещё парочка четырёхмерных (точнее, многомерных) языков. Оба — диалекты BrainFuck. Но в одном каретка блуждает по многомерной памяти, а программа выглядит, как строчка на BF, а в другом наоборот — программа многомерна, зато память линейна. Отличие от 4DL — что в обоих случаях управление и работа с памятью разделены.
Ссылки.
Страничка 4DL на esolang
Страничка из блога автора
Сайт с интерпретатором
Befunge и его диалекты
Brainfuck с многомерной памятью
Brainfuck с многомерной программой