Comments 38
Вспомнился мой любимый — парадокс маляра. Бесконечную поверхность можно покрасить конечным количеством краски. С теорвером этот парадокс не связан.
Бесконечно тонким слоем??
Но слой же не может быть тоньше размера атома!
Или я сильно неправ?
Но слой же не может быть тоньше размера атома!
Или я сильно неправ?
Я думаю имеются ввиду поверхности вроде сферы по которым двумерным существам можно бегать бесконечно. Или что-то типа односторонних поверхностей вида ленты Мебиуса или бутылки Клейна.
Там всё хитрее. Там объём тела врещения от фигуры бесконечной площади конечен. ru.wikipedia.org/wiki/Парадокс_маляра
Да, простите. Был не прав.
Лолчто?? кто о чем, а я о физике!=)
если отбросить всю абстракцию(которая, кстати, не оговорена в условиях задачи), то с тех пор, когда бесконечно длинный цилиндр начнет иметь диаметр меньше размера атома, краска тупо не будет туда пролазить!!!)))))))
парадокс вовсе и не парадокс даже)
upd: Черт, на вики все об этом написано, посыпаю голову пеплом
если отбросить всю абстракцию(которая, кстати, не оговорена в условиях задачи), то с тех пор, когда бесконечно длинный цилиндр начнет иметь диаметр меньше размера атома, краска тупо не будет туда пролазить!!!)))))))
парадокс вовсе и не парадокс даже)
upd: Черт, на вики все об этом написано, посыпаю голову пеплом
<комментарий не в ту ветку>
8/(3+8) = 0.7272727272727?
P(взято из правой|был быбран красный шарик)=P(взят красный шарик|была выбрана правая рука)*P(выбрана правая рука)/P(выбран красный шарик)
(8/13)*(1/2)/(11/23)=~0,6434
(8/13)*(1/2)/(11/23)=~0,6434
1/2 * (3/10 + 8/13) = 11/23? интересно…
Разве при такой постановке задачи, как в условии, P(взят красный шарик) не достоверное событие?
И вообще мудрите вы по моему все)
Я вот не вижу почему ответ не 8/11, это же очевидно.
Для любителей собственно формулы Байеса:
Условие:
P(крас|прав) = 8/13
P(крас|левая) = 3/10
P(правая) = 13/23
P(левая) = 10/23
Решение:
P(прав|крас) = P(крас|прав) ∗ P(прав) / ( P(крас|прав) ∗ P(прав) + P(крас|левая) ∗ P(левая)) =
8/13 * 13/23 / ( 8/13 * 13/23 + 3/10 * 10/23 ) = 8/11
Я вот не вижу почему ответ не 8/11, это же очевидно.
Для любителей собственно формулы Байеса:
Условие:
P(крас|прав) = 8/13
P(крас|левая) = 3/10
P(правая) = 13/23
P(левая) = 10/23
Решение:
P(прав|крас) = P(крас|прав) ∗ P(прав) / ( P(крас|прав) ∗ P(прав) + P(крас|левая) ∗ P(левая)) =
8/13 * 13/23 / ( 8/13 * 13/23 + 3/10 * 10/23 ) = 8/11
Хм, модель выбора важнее, чем казалось.
Две открытые ладони равной площади, с небольшим промежутком между ними. Выбор производится с закрытыми глазами. Щепоть изначально расположена над промежутком между ладонями. Дрожащая щепоть опускается вертикально вниз, попадая на край одной или другой ладони. После этого, на этой ладони, щепоть находит ближайшую пилюлю. Выбор совершен.
8/13 * 1/2 / ( 8/13 * 1/2 + 3/10 * 1/2 ) = 80/119
т.е. вариант 2 от Kerogi и по простому расчету от Mrrl
Две открытые ладони равной площади, с небольшим промежутком между ними. Выбор производится с закрытыми глазами. Щепоть изначально расположена над промежутком между ладонями. Дрожащая щепоть опускается вертикально вниз, попадая на край одной или другой ладони. После этого, на этой ладони, щепоть находит ближайшую пилюлю. Выбор совершен.
8/13 * 1/2 / ( 8/13 * 1/2 + 3/10 * 1/2 ) = 80/119
т.е. вариант 2 от Kerogi и по простому расчету от Mrrl
У меня ответ 119/260 -> 0.4576… Где правильный ответ?
Всего красных 11. В 1 группе 3, во 2 — 8.
Берём случайным образом.
Вероятность, что она из 2 группы — 8/11.
Берём случайным образом.
Вероятность, что она из 2 группы — 8/11.
У меня получилось 80/119 = (8/13)/(8/13+3/10). Конечно, при условии, что априорно руки равновероятны.
Условие задачи не очень корректно поставлено (или при переводе корректность потерялась).
Здесь может быть два варианта.
Вариант 1.
Морфеус выкладывает из рук на стол все таблетки (но на таблетках остаются метки в какой руке она была), и вы выбираете из общей кучи.
Этот вариант и подразумевается, потому что это задача на смесь распределений.
Сначала есть два распределения (в разных руках), которые перемешиваются, и выбор делается из смеси.
Вариант 2.
Вы выбираете руку (например, не глядя — Морфеус протягивает одну из них и спрашивает «Эта?», а вы говорите да или нет), и потом выбираете наугад в ней таблетку.
Здесь выбор в два этапа — байесовская сеть.
Для этих условий ответы будут совершенно разные.
Здесь может быть два варианта.
Вариант 1.
Морфеус выкладывает из рук на стол все таблетки (но на таблетках остаются метки в какой руке она была), и вы выбираете из общей кучи.
Этот вариант и подразумевается, потому что это задача на смесь распределений.
Сначала есть два распределения (в разных руках), которые перемешиваются, и выбор делается из смеси.
Вариант 2.
Вы выбираете руку (например, не глядя — Морфеус протягивает одну из них и спрашивает «Эта?», а вы говорите да или нет), и потом выбираете наугад в ней таблетку.
Здесь выбор в два этапа — байесовская сеть.
Для этих условий ответы будут совершенно разные.
Поправьте меня если я не прав:
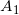 — левая рука (событие)
— левая рука (событие)
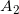 — правая рука (событие)
— правая рука (событие)
Соответственно вероятности: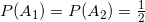
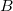 — попался красный шарик (событие)
— попался красный шарик (событие)
Если бы Морфеус высыпал все шарики на стол со следами правой и левой руки (Вариант 1) то вероятность выбора красного шарика была бы:
Вероятность что в левой руке мы найдем красный шарик: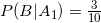 ; что в правой:
; что в правой: 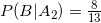
Для варианта 2, когда Морфеус оставил таблетки у себя, вероятность(общая) выбора красного шарика будет:
Соответственно, что при выборе красного шарика вероятность того, что он побывал в правой руке (Вариант 1):
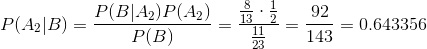
Для варианта 2:
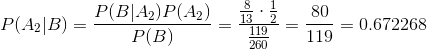
И тут напрашивается два вывода:
1) Если Морфеус высыпет шарики на стол, то вероятность выбора красного шарика выше, чем если бы он их держал в руках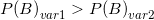
2) Если Морфеус держит шарики в руках, в том количестве и соотношении как указанно в условии, то при выборе в слепую красного шарика он будет из правой руки чаще чем если бы он высыпал их: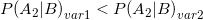
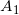 — левая рука (событие)
— левая рука (событие)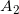 — правая рука (событие)
— правая рука (событие)Соответственно вероятности:
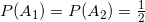
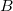 — попался красный шарик (событие)
— попался красный шарик (событие)Если бы Морфеус высыпал все шарики на стол со следами правой и левой руки (Вариант 1) то вероятность выбора красного шарика была бы:

Вероятность что в левой руке мы найдем красный шарик:
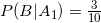 ; что в правой:
; что в правой: 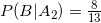
Для варианта 2, когда Морфеус оставил таблетки у себя, вероятность(общая) выбора красного шарика будет:
Соответственно, что при выборе красного шарика вероятность того, что он побывал в правой руке (Вариант 1):
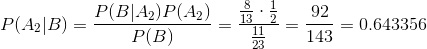
Для варианта 2:
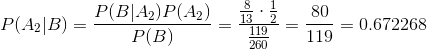
И тут напрашивается два вывода:
1) Если Морфеус высыпет шарики на стол, то вероятность выбора красного шарика выше, чем если бы он их держал в руках
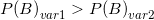
2) Если Морфеус держит шарики в руках, в том количестве и соотношении как указанно в условии, то при выборе в слепую красного шарика он будет из правой руки чаще чем если бы он высыпал их:
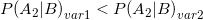
Я очень быстро, потому что чесслово сейчас некогда.
Если интересно, я подробно разберу чуть позже.
У вас небольшая ошибка, на которую я тоже наткнулся, когда решал, потому что условие запутало (я его понял как вариант 2).
Дело в том, что в варианте 1 вероятности рук разные :)
Т.к. в левой руке 10 таблеток, а в правой 13, то после высыпания на стол вероятность взять таблетку, которая была в левой руке 10/23, а в правой 13/23.
Во втором варианте вероятности равны — по 1/2 (если конечно, у Морфеуса руки не отличаются с точки зрения выбора :))
Попробуйте пересчитать с учетом этого.
Если интересно, я подробно разберу чуть позже.
У вас небольшая ошибка, на которую я тоже наткнулся, когда решал, потому что условие запутало (я его понял как вариант 2).
Дело в том, что в варианте 1 вероятности рук разные :)
Т.к. в левой руке 10 таблеток, а в правой 13, то после высыпания на стол вероятность взять таблетку, которая была в левой руке 10/23, а в правой 13/23.
Во втором варианте вероятности равны — по 1/2 (если конечно, у Морфеуса руки не отличаются с точки зрения выбора :))
Попробуйте пересчитать с учетом этого.
Ок, чуть разгрёбся.
Короче говоря, в первом случае вероятность равна 8/11 ~ 0.(72) — 72 в периоде.
Что какбэ намекает на распределение красных шариков между руками — 8 в одной и 3 в другой ;)
Потому что при высыпании происходит перемешивание экземпляров разных распределений и фактически количество синих не влияет.
То есть, когда происходит событие выбран красный шарик, то происходит срезка пространства исходов эксперимента по оси «Цвет шарика», и тогда начинает работать условное распределение «Какая рука при условии, что выбран красный шарик» или математически (Рука|Цвет=Красный).
Поэтому ответы на вопросы (с точностью до результата в варианте 1)
1) Вероятность выбора красного при высыпании на стол больше (0,73 > 0,67), так как в случае варианта 2 (с первоначальным выбором руки) влияют синие шарики, то есть, неравномерность распределения в отношении красных и синих для разных рук.
Красный шарик в левой руке «стоит» дороже, потому что в левой руке общее количество шариков (с учетом синих) меньше.
Может быть сильнее запутал, просто тут идея в том, что среднее арифметическое отношений не равно отношению сумм.
(половина одной пропорции + половина другой пропорции <> общей пропорции)
В этом как раз состоит Байес — перевзвес вероятностей как отношений не происходит простым переносом (суммированием и вычитанием) исходов.
2) Вероятность получения шарика из правой руки выше в варианте с высыпанием, чем с выбором руки, потому что:
а) шариков в правой руке больше — для варианта 1 вероятность попадания в шарик из правой руки P(A2) больше по сравнению с равномерным распределением
б) есть неравномерность распределений в разных руках, и с учетом этого вероятность получения красного шарика P(B) в варианте 2 меньше, но она падает медленнее, чем растет вероятность правой руки в варианте 1 (см. пункт а),
поэтому общее отношение в конечном итоге в варианте 1 больше, и следовательно, итоговая условная вероятность правой руки при выпадении красного шарика будет больше.
P.S. Совет — обозначать исходы буквами, привязанными к исходам.
Например, для данного случая будут такие исходы — П, Л, К, С
Тогда вопрос задачи будет читаться как P(П|К) — вероятность Правой руки при условии Красного шарика.
Ну и другие варианты P(^K) — вероятность НеКрасного шарика, то есть, вероятность синего.
Удобнее не путаться :)
Короче говоря, в первом случае вероятность равна 8/11 ~ 0.(72) — 72 в периоде.
Что какбэ намекает на распределение красных шариков между руками — 8 в одной и 3 в другой ;)
Потому что при высыпании происходит перемешивание экземпляров разных распределений и фактически количество синих не влияет.
То есть, когда происходит событие выбран красный шарик, то происходит срезка пространства исходов эксперимента по оси «Цвет шарика», и тогда начинает работать условное распределение «Какая рука при условии, что выбран красный шарик» или математически (Рука|Цвет=Красный).
Поэтому ответы на вопросы (с точностью до результата в варианте 1)
1) Вероятность выбора красного при высыпании на стол больше (0,73 > 0,67), так как в случае варианта 2 (с первоначальным выбором руки) влияют синие шарики, то есть, неравномерность распределения в отношении красных и синих для разных рук.
Красный шарик в левой руке «стоит» дороже, потому что в левой руке общее количество шариков (с учетом синих) меньше.
Может быть сильнее запутал, просто тут идея в том, что среднее арифметическое отношений не равно отношению сумм.
(половина одной пропорции + половина другой пропорции <> общей пропорции)
В этом как раз состоит Байес — перевзвес вероятностей как отношений не происходит простым переносом (суммированием и вычитанием) исходов.
2) Вероятность получения шарика из правой руки выше в варианте с высыпанием, чем с выбором руки, потому что:
а) шариков в правой руке больше — для варианта 1 вероятность попадания в шарик из правой руки P(A2) больше по сравнению с равномерным распределением
б) есть неравномерность распределений в разных руках, и с учетом этого вероятность получения красного шарика P(B) в варианте 2 меньше, но она падает медленнее, чем растет вероятность правой руки в варианте 1 (см. пункт а),
поэтому общее отношение в конечном итоге в варианте 1 больше, и следовательно, итоговая условная вероятность правой руки при выпадении красного шарика будет больше.
P.S. Совет — обозначать исходы буквами, привязанными к исходам.
Например, для данного случая будут такие исходы — П, Л, К, С
Тогда вопрос задачи будет читаться как P(П|К) — вероятность Правой руки при условии Красного шарика.
Ну и другие варианты P(^K) — вероятность НеКрасного шарика, то есть, вероятность синего.
Удобнее не путаться :)
Почему я не удивлен, что самой обсуждаемой частью статьи является задача с Морфеусом?
А давайте тогда обсудим какой-нибудь парадокс.
Мне вот, например, очень интересно, как звучит парадокс ворона в строгом смысле, потому что если жонглировать словами, как это делается в русскоязычной (в англоязычной, кстати, тоже) википедии, получается какая-то чепуха.
Почему утверждение «все вороны чёрные» отождествляется с эквивалентностью понятий «ворон» и «чёрный»?
Мне вот, например, очень интересно, как звучит парадокс ворона в строгом смысле, потому что если жонглировать словами, как это делается в русскоязычной (в англоязычной, кстати, тоже) википедии, получается какая-то чепуха.
Предположим, что существует теория, согласно которой все вороны чёрные. Согласно формальной логике, эта теория эквивалентна теории, что все предметы, не являющиеся чёрными, не являются воронами.
Почему утверждение «все вороны чёрные» отождествляется с эквивалентностью понятий «ворон» и «чёрный»?
Тут не эквивалентность, а отношение причины и следствия.
Если ворон, то чёрный.
Если не чёрный, то не ворон.
Вот эти выражения эквивалентны.
Если ворон, то чёрный.
Если не чёрный, то не ворон.
Вот эти выражения эквивалентны.
Я обращаю ваше внимание на то, что тут в формулировке присутствует ловушка естественного языка (например, когда мы опускаем повторяющиеся слова, но подразумеваем, что они относятся ко всем элементам перечисления). Вероятно, парадокс и без неё существует.
Так вот, в записи «если ворон, то чёрный» у вас слева (причина) существительное, а справа (следствие) прилагательное. Вы можете переписать это выражение так, чтобы с обоих сторон стояли одинаковые части речи?
«Чёрный» в данном случае не просто утверждение, а одноместный предикат (или свойство, или функция с областью значений {ложь, истина}), заданный на множестве воронов. Причём, вне этих самых воронов этот предикат теряет всякий смысл, т.к. выходит за область определения. А в рамках области определения «если ворон, то чёрный» — тривиальное тождество, вырожденный случай.
И для того, чтобы дальше что-то искать и как-то оценивать, нужно оцениваемую функцию определить на всей области, где мы её применяем. А вот если записать так: «Для каждого предмета из (яблоки, вороны): если предмет из (вороны), то чёрный(предмет)=истина; если предмет из (яблоки), то чёрный(предмет)=ложь.», но тогда у нас получается, что мы опять всё знаем до того, как вопрос будет задан.
По-моему, самое главное — это отсечь всякие ложные аналогии и ту вольность, которую позволяют естественные языки, и в самом начале подобных изысканий постулировать:
Если какое-либо свойство не наблюдалось у объекта (имеется в виду применимость одноместного предиката), то невозможно сказать, обладает ли объект данным свойством (т.е. применим ли одноместный предикат).
А дальше остается только призвать на помощь остатки мужества и запретить использовать операции там, где они не определены.
В той же вики-статье есть упоминание, что принцип индукции утверждает:
Эта формулировка расстраивает Карла Поппера (но, думаю, он не имел ничего против строгого математического определения принципа индукции):

А вот Дилберт недоумевает по этому поводу:

Так вот, в записи «если ворон, то чёрный» у вас слева (причина) существительное, а справа (следствие) прилагательное. Вы можете переписать это выражение так, чтобы с обоих сторон стояли одинаковые части речи?
«Чёрный» в данном случае не просто утверждение, а одноместный предикат (или свойство, или функция с областью значений {ложь, истина}), заданный на множестве воронов. Причём, вне этих самых воронов этот предикат теряет всякий смысл, т.к. выходит за область определения. А в рамках области определения «если ворон, то чёрный» — тривиальное тождество, вырожденный случай.
И для того, чтобы дальше что-то искать и как-то оценивать, нужно оцениваемую функцию определить на всей области, где мы её применяем. А вот если записать так: «Для каждого предмета из (яблоки, вороны): если предмет из (вороны), то чёрный(предмет)=истина; если предмет из (яблоки), то чёрный(предмет)=ложь.», но тогда у нас получается, что мы опять всё знаем до того, как вопрос будет задан.
По-моему, самое главное — это отсечь всякие ложные аналогии и ту вольность, которую позволяют естественные языки, и в самом начале подобных изысканий постулировать:
Если какое-либо свойство не наблюдалось у объекта (имеется в виду применимость одноместного предиката), то невозможно сказать, обладает ли объект данным свойством (т.е. применим ли одноместный предикат).
А дальше остается только призвать на помощь остатки мужества и запретить использовать операции там, где они не определены.
В той же вики-статье есть упоминание, что принцип индукции утверждает:
Наблюдение явления Х, которое соответствует теории Т, увеличивает вероятность того, что теория Т истинна.
Эта формулировка расстраивает Карла Поппера (но, думаю, он не имел ничего против строгого математического определения принципа индукции):

А вот Дилберт недоумевает по этому поводу:

Да нет тут особо никакой ловушки.
Переформулировать можно так.
Если объект имеет для свойства «Ворон?» значение ИСТИНА, то значение свойства «Черный?» равно ИСТИНА.
Если значение свойства «Черный?» равно ЛОЖЬ, то значение свойства «Ворон?» равно ЛОЖЬ.
Так подходит? И все конъюнкции-дизъюнкции работают.
Переформулировать можно так.
Если объект имеет для свойства «Ворон?» значение ИСТИНА, то значение свойства «Черный?» равно ИСТИНА.
Если значение свойства «Черный?» равно ЛОЖЬ, то значение свойства «Ворон?» равно ЛОЖЬ.
Так подходит? И все конъюнкции-дизъюнкции работают.
Иначе говоря, любой факт, кроме наблюдения не чёрного ворона, подтверждает теорию о том, что вороны чёрные.
Небольшая поправка — вместо «подтверждает» здесь нужно «не опровергает».
Потому что независимые факты на доказательство теории не влияют, и вероятность ее правильности не меняется (теория не подтверждается и не опровергается).
Да, так подходит. Спасибо, при такой записи всё становится гораздо более понятным.
«Так все-таки — красную или синюю? Красную или синюю?.. Эх Морфеус, Морфеус, где же ты, когда ты так нужен...»
Хмм. А ответ то какой? Где вы, Байессиане?
Мы выбрали руку. Например, с завязанными глазами раскрутились вокруг своей оси и нам подсунули кучку пилюль из руки более близкой к нашему левому плечу. Если равноудалены то покрутились еще до достижения эффекта.
Вероятность выбора правой руки равна 0.5 до вытягивания пилюли.
Мы вытянули пилюлю. Она оказалась именно красной.
Вероятность выбрать красную, а не синюю таблетку из правой 0,615
Из левой руки 0,3
Хотелось бы воспользоваться формулой
P(правая)=0,5; P(~правая) 0,5; 1 степень свободы.
P(красная/правая)=0,615
P(красная/~правая)=0,3
P(красная) = P(красная/правая)*P(правая)+ P(красная/~правая)*P(~правая) = 0.458
P(правая/красная) = (P(красная/правая)* P(правая))/P(красная)
Итого вероятность правой руки при вытягивании красной пилюли 0,671
Где ошибка?
Пилюли из разных рук не перемешивались.
Мы выбрали руку. Например, с завязанными глазами раскрутились вокруг своей оси и нам подсунули кучку пилюль из руки более близкой к нашему левому плечу. Если равноудалены то покрутились еще до достижения эффекта.
Вероятность выбора правой руки равна 0.5 до вытягивания пилюли.
Мы вытянули пилюлю. Она оказалась именно красной.
Вероятность выбрать красную, а не синюю таблетку из правой 0,615
Из левой руки 0,3
Хотелось бы воспользоваться формулой
P(правая)=0,5; P(~правая) 0,5; 1 степень свободы.
P(красная/правая)=0,615
P(красная/~правая)=0,3
P(красная) = P(красная/правая)*P(правая)+ P(красная/~правая)*P(~правая) = 0.458
P(правая/красная) = (P(красная/правая)* P(правая))/P(красная)
Итого вероятность правой руки при вытягивании красной пилюли 0,671
Где ошибка?
Пилюли из разных рук не перемешивались.
Sign up to leave a comment.
Байес