Comments 118
Доказательство девятой задачи похоже на доказательство теоремы:
Для любого алгоритма сжатия без потерь и любого наперед заданного числа N существует строка длины N, которую алгоритм сжать не сможет.
Для любого алгоритма сжатия без потерь и любого наперед заданного числа N существует строка длины N, которую алгоритм сжать не сможет.
>вылетает муха со скоростью 200 км/ч
дальше не читал, не вижу смысла…
дальше не читал, не вижу смысла…
есть громадная разница между задачами на релятивистское движение и обычное не релятивистское движение, реальных объектов которые движутся со скоростями близкими к скорости света в вселенной не самое большое количество + задача данного ресурса популяризация науки, а эта обычная олимпиадная задача
при составлении физических задач для решебника обычно думают о реальности данных (не удивлюсь что рано или поздно ребенок решит что муха летает с такой скоростью), но иногда появляются такие задачи что аж Задорнов не стесняется их взять себе в номер:
при составлении физических задач для решебника обычно думают о реальности данных (не удивлюсь что рано или поздно ребенок решит что муха летает с такой скоростью), но иногда появляются такие задачи что аж Задорнов не стесняется их взять себе в номер:
Из учебника физики за 8 класс, под ред. С. В. Громова. Задача No 109.
«В озеро упала ветка. Пробегавший мимо олень успел заметить, что волна, созданная падением ветки, дошла до берега за 10 с, причём расстояние между соседними гребнями волн было равно 10 см и за 2 с было 4 всплеска о берег. Помогите оленю определить, как далеко от берега упала ветка».
муха-робот?
в данной задаче с мухой не вижу ничего страшного — это вполне обычный «отход от реальности» и при желании ее можно подогнать под реальность, а вот про задачу из учебника спорить не будут — это позорище. в статье, в конце-концов, ни слова о том, что это задачи из учебника какого-нибудь?
ссылку дал исключительно для того, чтобы показать, что иногда подобные отходы от привычностей и реальности могут давать довольно интересные ответы (о чем, кстати, сам xkcd говорил на TED)
в данной задаче с мухой не вижу ничего страшного — это вполне обычный «отход от реальности» и при желании ее можно подогнать под реальность, а вот про задачу из учебника спорить не будут — это позорище. в статье, в конце-концов, ни слова о том, что это задачи из учебника какого-нибудь?
ссылку дал исключительно для того, чтобы показать, что иногда подобные отходы от привычностей и реальности могут давать довольно интересные ответы (о чем, кстати, сам xkcd говорил на TED)
>в данной задаче с мухой не вижу ничего страшного — это вполне обычный «отход от реальности»
реальность около 6-7 км/ч, а тут отличие на порядок (а это многовато) + данные для поездов не завышенны
>в статье, в конце-концов, ни слова о том, что это задачи из учебника какого-нибудь?
беглый гуглинг говорит про возможного автора Н. Я. Виленкина (http://www.e-reading.ws/bookreader.php/97471/Pavlov_-_Matematicheskie_olimpiady_po_ligam._5-9_klassy.html)
отсутствие ссылок на источники в статье удручает
>ссылку дал исключительно для того…
это популяризация науки, это другое
ps what-if.xkcd.com по русски -> chtoes.li
реальность около 6-7 км/ч, а тут отличие на порядок (а это многовато) + данные для поездов не завышенны
>в статье, в конце-концов, ни слова о том, что это задачи из учебника какого-нибудь?
беглый гуглинг говорит про возможного автора Н. Я. Виленкина (http://www.e-reading.ws/bookreader.php/97471/Pavlov_-_Matematicheskie_olimpiady_po_ligam._5-9_klassy.html)
отсутствие ссылок на источники в статье удручает
>ссылку дал исключительно для того…
это популяризация науки, это другое
ps what-if.xkcd.com по русски -> chtoes.li
реальность около 6-7 км/ч, а тут отличие на порядок (а это многовато) + данные для поездов не завышенны
и? вот и отход от реальности, в чем проблема? где-то написано, что увеличение реальных данных на порядок — очень плохо?
вот вам новый вариант задачи, из близкого будущего :)
2032 год. Из китайских городов A и B, расстояние между которыми 100 км, одновременно навстречу друг другу выезжают два высокоскоростных поезда, их скорости 400 км/ч и 600 км/ч соответственно. Одновременно из города А в направлении B вылетает муха-робот со скоростью 200 км/ч, летит до встречи с поездом, выехавшим из B… Какое расстояние пролетит муха до того, как поезда встретятся?
отсутствие ссылок на источники в статье удручает
мне кажется, что
>в чем проблема?
проблема в понятии материальной точки и в том что оно нормально укладывается только к 8 классу, в 5 классе дети хорошо понимают как «лисичка бегает за зайчиком». + при этом учитель может оказатся в очень глупой ситуации когда ребенок спросит «а почему муха летит быстрее поезда»
>их скорости 400 км/ч и 600 км/ч соответственно муха-робот со скоростью 200 км/ч
суть задачи потерялась, тк скорость мухи должна быть >> скоростей поездов
поезда можно было бы заменить на катера, а муху на вертолёт и всё сразу стало бы нормально
проблема в понятии материальной точки и в том что оно нормально укладывается только к 8 классу, в 5 классе дети хорошо понимают как «лисичка бегает за зайчиком». + при этом учитель может оказатся в очень глупой ситуации когда ребенок спросит «а почему муха летит быстрее поезда»
>их скорости 400 км/ч и 600 км/ч соответственно муха-робот со скоростью 200 км/ч
суть задачи потерялась, тк скорость мухи должна быть >> скоростей поездов
поезда можно было бы заменить на катера, а муху на вертолёт и всё сразу стало бы нормально
Вы учитель? Дети бывают разные — кто-то и в 11 классе понимает хорошо только как «лисичка бегает за зайчиком»
естественно потерялась, зато соответствует реальности, ведь так? :)
суть задачи потерялась, тк скорость мухи должна быть >> скоростей поездов
естественно потерялась, зато соответствует реальности, ведь так? :)
Пишут, что скорость полёта слепня до 60 км/ч, это уже не так сильно отличается от условия. Можно заменить муху на стрижа, который действительно летает на скорости 200 км/ч.
Я не задавался целью подсадить читателей на олимпиадные задачи, но напомнить об интересных темах, которые есть даже в школьной программе: бином Ньютона, геометрические прогрессии, принцип Дирихле и другие. Хорошо, когда мозги работают. А в задаче про муху просто нужна сообразительность.
Я не задавался целью подсадить читателей на олимпиадные задачи, но напомнить об интересных темах, которые есть даже в школьной программе: бином Ньютона, геометрические прогрессии, принцип Дирихле и другие. Хорошо, когда мозги работают. А в задаче про муху просто нужна сообразительность.
>что скорость полёта слепня до 60 км/ч
мгновенная и средняя скорости это разные скорости
мгновенная и средняя скорости это разные скорости
господи, да вы зануднее меня на порядок и это очень плохо :)
wildwildworld.net.ua/articles/samye-bystrye-sushchestva
Абсолютным рекордсменом по скорости передвижения является — сапсан. Эта птица способна развивать скорость выше 200 км/ч при полете по прямой. А в пикирующем полете во время охоты сапсан способен разогнаться до 325 км/ч(это даже быстрее, чем многие спортивные автомобили именитых марок)!
wildwildworld.net.ua/articles/samye-bystrye-sushchestva
>господи, да вы зануднее меня на порядок и это очень плохо :)
нужно закругляться, bcove.me/1xwb2ne8 ;)
нужно закругляться, bcove.me/1xwb2ne8 ;)
Замените уже на беспилотник, который пытается определить, в каком из поездов едет ...( подставить: Джеймс Бонд, террорист, дед-мороз и так далее по желанию :))
А ник-то как в тему.
Задача-ловушка. Правило «в семье ровно один мальчик» никак не влияет на вероятность рождения мальчика в целом в стране.Больше всего думал здесь, но так и не понял в чём именно заключается ловушка. Поясните подробнее?
Условие составлено так, что может показаться, что будет больше мальчиков или девочек. Правило «последний ребенок в семье — мальчик» является лишним условием, сбивающим с толку.
Некоторые рассуждают, что раз мальчик есть в каждой семье, то мальчиков всего должно быть больше. Есть и противоположное мнение: до первого мальчика может родиться сколько угодно девочек, значит девочек будет больше. Кое-кто даже вспомнит геометрическое распределение и рассчитает математическое ожидание числа детей в семье как 1 / 0.5 = 2, и сделает верный вывод, что в среднем в семье будет по 2 ребенка, то есть 1 мальчик и 1 девочка.
Однако это всё не требуется для решения задачи, так как на распределение мальчиков и девочек в стране не влияет то, в какой семье их родили. Это правило (последний ребенок в семье — мальчик) не изменяет того, что мальчики и девочки рождаются поровну. То есть, ответ содержится практически в условии: 50% мальчиков, 50% девочек.
Некоторые рассуждают, что раз мальчик есть в каждой семье, то мальчиков всего должно быть больше. Есть и противоположное мнение: до первого мальчика может родиться сколько угодно девочек, значит девочек будет больше. Кое-кто даже вспомнит геометрическое распределение и рассчитает математическое ожидание числа детей в семье как 1 / 0.5 = 2, и сделает верный вывод, что в среднем в семье будет по 2 ребенка, то есть 1 мальчик и 1 девочка.
Однако это всё не требуется для решения задачи, так как на распределение мальчиков и девочек в стране не влияет то, в какой семье их родили. Это правило (последний ребенок в семье — мальчик) не изменяет того, что мальчики и девочки рождаются поровну. То есть, ответ содержится практически в условии: 50% мальчиков, 50% девочек.
Как это не влияет, если число семей конечно.
Так как мне не интуитивно понятно ваше объяснение я все посчитал:
Какие в семье могут быть варианты:
М, ДМ, ДДМ, ДДДМ,…
Посчитаем вероятности этих вариантов:
М — 1/2 — 0 девочек
ДМ — 1/4 — 1 девочка
ДДМ — 1/8 — 2 девочки
ДДД...n штук… ДМ — 1/2^(n+1) — n девочек
Понятно, что количество мальчиков всегда равно 1.
Считаем среднее значение количества девочек:
0*1/2 + 1*1/4 + 2*1/8 +… + n*1/2^(n+1) +… = sum(n/2^(n+1)) = 1.
Доля мальчиков — 1/2. Ч.т.д.
Какие в семье могут быть варианты:
М, ДМ, ДДМ, ДДДМ,…
Посчитаем вероятности этих вариантов:
М — 1/2 — 0 девочек
ДМ — 1/4 — 1 девочка
ДДМ — 1/8 — 2 девочки
ДДД...n штук… ДМ — 1/2^(n+1) — n девочек
Понятно, что количество мальчиков всегда равно 1.
Считаем среднее значение количества девочек:
0*1/2 + 1*1/4 + 2*1/8 +… + n*1/2^(n+1) +… = sum(n/2^(n+1)) = 1.
Доля мальчиков — 1/2. Ч.т.д.
Хм. Вы смело отбросили вероятность того, что последней (на текущий момент) может родится девочка. Думаю вот так будет нагляднее
Согласен с вашим вариантом подсчёта количества в среднем мальчиков:
Nm = sum[P(Di) * P(M)]
Nm — количество мальчиков
P(Di) — вероятность рождения ребёнка в i-м поколении
P(M) — вероятность рождения мальчика
Nm = 1*1/2 + 1/2 * 1/2 + 1/4 * 1/2 = сумм(1/2^(n+1) ) = 1
А девочек в среднем будет
Nf = sum[P(Di) * P(F)] + sum[P(Di) * Nf(i)]
Из непонятного тут Nf(i) — кол-во девочек в этом поколении
Первая составляющая эквивалентна кол-ву мальчиков. Те — 1
Вторая часть будет sum[P(Di) * Nf(i)] = (собственно вы это и посчитали уже) = 1
Общая же значение будет в среднем 2 девочки в семье.
Т.е. соотношение будет один мальчик к двум девочкам.
Поколение Вероятность рождения ребёнка в этом поколении Количество уже рождённых девочек Вероятность рождения мальчика
1 100% 0 50%
2 50% 1 50%
3 25% 2 50%
4 12.5% 3 50%
Согласен с вашим вариантом подсчёта количества в среднем мальчиков:
Nm = sum[P(Di) * P(M)]
Nm — количество мальчиков
P(Di) — вероятность рождения ребёнка в i-м поколении
P(M) — вероятность рождения мальчика
Nm = 1*1/2 + 1/2 * 1/2 + 1/4 * 1/2 = сумм(1/2^(n+1) ) = 1
А девочек в среднем будет
Nf = sum[P(Di) * P(F)] + sum[P(Di) * Nf(i)]
Из непонятного тут Nf(i) — кол-во девочек в этом поколении
Первая составляющая эквивалентна кол-ву мальчиков. Те — 1
Вторая часть будет sum[P(Di) * Nf(i)] = (собственно вы это и посчитали уже) = 1
Общая же значение будет в среднем 2 девочки в семье.
Т.е. соотношение будет один мальчик к двум девочкам.
Наличие семей, в которых есть только девочки, а мальчик пока не родился, усложняет решение задачи через рассмотрение распределения мальчиков и девочек в семьях. Вероятность смерти родителей до рождения мальчика не задана. Задерка между рождением детей тоже влияет на текущее распределение детей в семьях.
>> Наличие семей, в которых есть только девочки, а мальчик пока не родился, усложняет решение задачи через рассмотрение распределения мальчиков и девочек в семьях.
Собственно определить среднее отношение мальчиков и девочек в семье и является условием задачи. Нигде же не сказано что все семьи уже родили всех своих детей, как-раз наоборот, все семьи находятся в процессе рождения детей, до тех пор пока не появится мальчик.
>> Вероятность смерти родителей до рождения мальчика не задана. Задержка между рождением детей тоже влияет на текущее распределение детей в семьях.
Не находите ли Вы странным, что все эти возможные условия оправданы условием задачи и замечательным образом решаются если учитывать, что последний ребёнок в семье мог ещё не родился? Может в этом кроется решение задачи?
Собственно определить среднее отношение мальчиков и девочек в семье и является условием задачи. Нигде же не сказано что все семьи уже родили всех своих детей, как-раз наоборот, все семьи находятся в процессе рождения детей, до тех пор пока не появится мальчик.
>> Вероятность смерти родителей до рождения мальчика не задана. Задержка между рождением детей тоже влияет на текущее распределение детей в семьях.
Не находите ли Вы странным, что все эти возможные условия оправданы условием задачи и замечательным образом решаются если учитывать, что последний ребёнок в семье мог ещё не родился? Может в этом кроется решение задачи?
Собственно определить среднее отношение мальчиков и девочек в семье и является условием задачи.В задаче спрашивается об отношении мальчиков и девочек в стране, а не в семье. Распределение мальчиков и девочек по семьям может принимать очень причудливый вид в зависимости от всех этих переменных, но ответ к задаче от этого не зависит, так как дети рождаются всё равно с вероятностями 50%.
Некоторые рассуждают, что раз мальчик есть в каждой семье, то мальчиков всего должно быть больше.Ну я примерно понял, что это имелось в виду под «ловушкой») Просто смутило дальнейшее выражение в кавычках, которое названо почему-то «правилом». Просто такие «ловушки» есть и в остальных задачах, на то они и занимательные.
Ну да, объяснение тут на самом деле очень простое как раз — правила того как семьи планируют своих детей, количества детей в разных семьях итд итп никак не влияют на вероятности рождения детей, очевидно (ведь опыт [тервер], заключающийся в рождении очередного ребёнка делается до всего этого и независимо от последующих действий). А эта вероятность рождения уже задана в условии.
Тоже не могу осмыслить. Мне кажется условие нужно учитывать. Влияние условия прямое же.
" семья производит на свет детей до первого мальчика", а не «последний ребенок в семье — мальчик».
Оно говорит именно о том, что в семье будет только один мальчик.
" семья производит на свет детей до первого мальчика", а не «последний ребенок в семье — мальчик».
Оно говорит именно о том, что в семье будет только один мальчик.
3я по мне показалась наиболее интересной и обманчивой, заключение в статье имхо «слегка» (т.е. совсем) неправильно. Вероятность рождение и родилось это вещи совершенно разные.
На деле имеем, в семье шанс родиться мальчику = 50%,
шанс рождения девочки равен 50% / n, где n — кол-во родившихся девочек (n > 0), для n = 0 шанс так же = 50%.
Т.е. имеем
Мальчики рождаются: 0.5*1 + 0.5*1 + 0.5*1 + 0.5*1 и т.д.
Девочки: 0.5*0 + 0.5 * 1 + 0.25 * 2 + 0.125 * 3 и т.д.
На деле имеем, в семье шанс родиться мальчику = 50%,
шанс рождения девочки равен 50% / n, где n — кол-во родившихся девочек (n > 0), для n = 0 шанс так же = 50%.
Т.е. имеем
Мальчики рождаются: 0.5*1 + 0.5*1 + 0.5*1 + 0.5*1 и т.д.
Девочки: 0.5*0 + 0.5 * 1 + 0.25 * 2 + 0.125 * 3 и т.д.
Основной подвох 3-ей задачи в том, что распределение мужского и женского населения зависит от вероятностей рождения мальчиков и девочек, но не зависит от того, когда семья прекращает рождение детей. Но даже если пойти сложным путём и рассчитывать математическое ожидание числа девочек в семье, то получим 1 девочку (геометрическое распределение, см. коментарий выше). Число мальчиков в семье фиксировано (1). Значит, в семье в среднем 1 девочка и всегда 1 мальчик, то есть общее число мальчиков и девочек в стране равно.
Нет, в стране может быть семья с 2 девочками и 1 мальчиком, а обратной семьи с 2 мальчиками и 1 девочкой не может быть.
При этом абсолютно верно что вероятность рождения мальчика и девочки одинаковая — и 1/2.
Получается в стране всегда будет перевес девочек. Посчитать математически я на работе не могу, Но ответ в статье к задаче не верен.
При этом абсолютно верно что вероятность рождения мальчика и девочки одинаковая — и 1/2.
Получается в стране всегда будет перевес девочек. Посчитать математически я на работе не могу, Но ответ в статье к задаче не верен.
Может быть семья вообще без девочек.
Таким образом, в среднем количество девочек будет равно количеству мальчиков
Таким образом, в среднем количество девочек будет равно количеству мальчиков
Ответ в статье к задаче верен.
Если мальчики и девочки рождаются с равными вероятностями, то как может быть перевес девочек?
Если мальчики и девочки рождаются с равными вероятностями, то как может быть перевес девочек?
семьи с 2 мальчиками и 1 девочкой не может бытьЗато может быть семья без девочек вообще: родился мальчик и всё, больше детей заводить им нельзя. А семьи, где есть только одна девочка и ноль мальчиков, не может быть.
В этом плане «обратной» семьёй «2 мальчика — 1 девочка» является составная семья «1 мальчик — 1 девочка» + «1 мальчик — 0 девочек».
З.Ы. Да, не обновил страницу перед комментом :)
З.Ы. Да, не обновил страницу перед комментом :)
На примере: есть 128 семей. Мальчик будет в каждой, т.е. их 128, они нас больше не интересуют.
Считаем девочек.
64 семей без девочек вообще.
32 семей с одной девочкой. 32 девочки.
16 семей с 2 девочками. 32+16*2=64 девочки
8 семей с 3 девочками. 32+16*3+8*3=88 девочек
4 семьи с 4 девочками. 32+16*3+8*3+4*4=104 девочки
2 семьи с 5 девочками. 114 девочек.
1 семья с 6, 120.
*половина семьи с 7 девочками, 123.5 девочек и т.д.*
Если семей больше, там будет предел, стремящийся к количеству семей. А при конечном количестве семей девочек будет несколько меньше.
Считаем девочек.
64 семей без девочек вообще.
32 семей с одной девочкой. 32 девочки.
16 семей с 2 девочками. 32+16*2=64 девочки
8 семей с 3 девочками. 32+16*3+8*3=88 девочек
4 семьи с 4 девочками. 32+16*3+8*3+4*4=104 девочки
2 семьи с 5 девочками. 114 девочек.
1 семья с 6, 120.
*половина семьи с 7 девочками, 123.5 девочек и т.д.*
Если семей больше, там будет предел, стремящийся к количеству семей. А при конечном количестве семей девочек будет несколько меньше.
64*0 + 32*1 + 16*2 + 8*3 + 4*4 + 2*5 + 1*6 + 7/2 + 8/4 + 9/8 + 10/16 + 11/32 + 12/64 = 127.78125
Сумма бесконечной геометрической прогрессии равна 128, значит математическое ожидание числа девочек всё-таки равно числу мальчиков при любом числе семей. А вот реальная доля (не ожидание) может отличаться от 50% (на то оно и распределение). Чтобы устремить долю мальчиков к 50%, нужно число семей и поколений устремить к бесконечности (число поколений, чтобы компенсировать возможный начальный перекос численности).
Сумма бесконечной геометрической прогрессии равна 128, значит математическое ожидание числа девочек всё-таки равно числу мальчиков при любом числе семей. А вот реальная доля (не ожидание) может отличаться от 50% (на то оно и распределение). Чтобы устремить долю мальчиков к 50%, нужно число семей и поколений устремить к бесконечности (число поколений, чтобы компенсировать возможный начальный перекос численности).
50% будет при бесконечном числе семей и потенциальных детей в семье.
Поскольку в реальности детей гораздо меньше бесконечности, девочек должно получиться всё-таки меньше.
Поскольку в реальности детей гораздо меньше бесконечности, девочек должно получиться всё-таки меньше.
Логика хромает. Хорошо это видно на примере одной или двух семей. Сколько этот подсчёт даёт для одной семьи (0 девочек?), для двух семей (1 девочку?).
Верное утверждение => семьи где мальчиков больше встречаются чаще (1 мальчик, 0 девочек). Зато девочки берут числом, как у моих знакомых: 5 девочек + 1 мальчик :)
Ловушка — методика подсчёта с семьями. Неверно, что будет 64 семьи без девочек, 32 семьи с одной девочкой,… — это возможное, но крайне невероятное событие.
P.S. интереса ради предлагаю провести численный эксперимент. Это не сложно, но никаких 127.78 девочек там не получится.
Верное утверждение => семьи где мальчиков больше встречаются чаще (1 мальчик, 0 девочек). Зато девочки берут числом, как у моих знакомых: 5 девочек + 1 мальчик :)
Ловушка — методика подсчёта с семьями. Неверно, что будет 64 семьи без девочек, 32 семьи с одной девочкой,… — это возможное, но крайне невероятное событие.
P.S. интереса ради предлагаю провести численный эксперимент. Это не сложно, но никаких 127.78 девочек там не получится.
«Неверно, что будет 64 семьи без девочек, 32 семьи с одной девочкой»
Это как раз верно.
Я свою ошибку понял.
«Мальчик будет в каждой, т.е. их 128, они нас больше не интересуют.»
Вот это не верно. В реальности будут семьи и только с девочками.
Допустим, в стране в среднем рожают 1 ребёнка. Получим 64 мальчика + 64 девочки.
Допустим, рожают 2 детей. Получим варианты — 1 ребёнок в семье (64 мальчика) или 2 ребёнка (32 мальчика + 96 девочек), суммарно по 96 каждых.
Допустим, рожают 3 детей. Получим варианты — 1 ребёнок в семье (64 мальчика), или 2 ребёнка (32 мальчика + 32 девочки), или 3 ребёнка (16 мальчиков + 80 девочек), суммарно 112 каждых.
Логику можно продолжить.
Так что мы либо рассматриваем вариант с конечным количеством детей в семье (тогда семьи без мальчиков приведут соотношение к 50%), либо с бесконечным и мальчиками в каждой семье (тогда маловероятные семьи с огромным количеством девочек приведут к 50%).
Это как раз верно.
Я свою ошибку понял.
«Мальчик будет в каждой, т.е. их 128, они нас больше не интересуют.»
Вот это не верно. В реальности будут семьи и только с девочками.
Допустим, в стране в среднем рожают 1 ребёнка. Получим 64 мальчика + 64 девочки.
Допустим, рожают 2 детей. Получим варианты — 1 ребёнок в семье (64 мальчика) или 2 ребёнка (32 мальчика + 96 девочек), суммарно по 96 каждых.
Допустим, рожают 3 детей. Получим варианты — 1 ребёнок в семье (64 мальчика), или 2 ребёнка (32 мальчика + 32 девочки), или 3 ребёнка (16 мальчиков + 80 девочек), суммарно 112 каждых.
Логику можно продолжить.
Так что мы либо рассматриваем вариант с конечным количеством детей в семье (тогда семьи без мальчиков приведут соотношение к 50%), либо с бесконечным и мальчиками в каждой семье (тогда маловероятные семьи с огромным количеством девочек приведут к 50%).
Доля девочек не зависит от распределения детей по семьям. Будем считать, что детей приносит аист. У него есть источник детей, где они появляются с вероятностью 50% мальчики и 50% девочки. Аист берет ребенка наугад и несет его в любую семью, где нет мальчика. Все дети в семьях — это бывшие дети в источнике, откуда их берет аист и где их поровну мальчиков и девочек. Распределение полов в семьях тоже совпадает с распределением полов в источнике.
Ну как сказать:
Усреднение по 10000 запускам даёт: 128 мальчиков, 128.3113 девочек. Исходный код:
{'boys': 128, 'girls': 116}
{'boys': 128, 'girls': 121}
{'boys': 128, 'girls': 127}
{'boys': 128, 'girls': 163}
{'boys': 128, 'girls': 127}
{'boys': 128, 'girls': 148}
{'boys': 128, 'girls': 140}
{'boys': 128, 'girls': 123}
{'boys': 128, 'girls': 138}
{'boys': 128, 'girls': 148}
Усреднение по 10000 запускам даёт: 128 мальчиков, 128.3113 девочек. Исходный код:
import random
def test(n):
boys = 0
girls = 0
for i in range(n):
while True:
if random.randint(0, 1) == 0:
break
girls += 1
boys += 1
return {'boys': boys, 'girls': girls}
if __name__ == '__main__':
for i in range(10):
print test(128)
Боюсь, ваш генератор недостаточно рандомный.
В python используется Mersenne Twister — очень неплохой генератор псевдослучайных чисел. Для этой задачи его должно за глаза хватать. 9.6. random — Generate pseudo-random numbers:
Python uses the Mersenne Twister as the core generator. It produces 53-bit precision floats and has a period of 2**19937-1. The underlying implementation in C is both fast and threadsafe. The Mersenne Twister is one of the most extensively tested random number generators in existence. However, being completely deterministic, it is not suitable for all purposes, and is completely unsuitable for cryptographic purposes.
На моём мониторе, вертикальная линия треугольника наклонена на 3 пикселя против часовой, горизонтальная на 2 пикселя по часовой. Не мог сосредоточится на задаче, так как угол должен быть прямым, а пиксели на мониторе прямоугольными. =) Ну и www.braingames.ru/ уже 8 лет отмечают.
Третья классная. Вроде кажется, что девочек должно быть больше, есть семьи с двумя-тремя и так далее девочками. Но все равное получается 50%.
Почему-то сразу (и в обед к тому же) вспомнился задачник Григория Остера )) А сколько вы сразу решили не залебнувшись от смеха?
N мудрецов выстроились «паровозиком», на каждого надели колпак белого или черного цвета.Никакого самоуважения у этих мудрецов…
мегаборода!
3. Если говорите строго, то ответ неверен. Строгий ответ: теория вероятности в аксиоматике Колмагорова оперирует набором последовательностей случайных величин. И в ее рамках да, ничего не меняется.
P.S.Однако данную задачу можно рассматривать аналогично знаменитой задаче с конвертом и вот тогда…
P.S.Однако данную задачу можно рассматривать аналогично знаменитой задаче с конвертом и вот тогда…
3. Если добавить, что население страны и число поколений стремятся к бесконечности, то решение (и условие) будет достаточно строгим.
P.S. Раз зашла речь про парадоксы, хочу поделиться самыми парадоксальными для меня: про конверты, парадокс Монти Холла, парадокс брадобрея, полная неожиданность. И ещё самая сложная логическая задача, хоть и не парадокс.
P.S. Раз зашла речь про парадоксы, хочу поделиться самыми парадоксальными для меня: про конверты, парадокс Монти Холла, парадокс брадобрея, полная неожиданность. И ещё самая сложная логическая задача, хоть и не парадокс.
Ну да, если рассмотривать случайную величину равную длине последовательности. Из условия задачи следует, что вероятность появление последовательности длины l равны 0.5^(-l)
В такой формулировке равенство мальчиков и девочек означает, что матожидание равно 2.
Ну а теперь надо посчитать сумму ряда l*0.5:(-l). Если честно, мне лень было выводить его руками я взял и подсчитал его численно. И да это двойка.
Однако я не уверен, что при другом подходе к задаче матожидание не измениться (на памяти задача с хордами или парадокс Бертрана)
В такой формулировке равенство мальчиков и девочек означает, что матожидание равно 2.
Ну а теперь надо посчитать сумму ряда l*0.5:(-l). Если честно, мне лень было выводить его руками я взял и подсчитал его численно. И да это двойка.
Однако я не уверен, что при другом подходе к задаче матожидание не измениться (на памяти задача с хордами или парадокс Бертрана)
Я могу вам ещё одну задачку подкинуть, в своё время на ней запоролись все участники олимпиады. Сформулирую по памяти, примерно: была построена лодка из дерева (плотность 750 кг/м3) размерами 3х1 метр. Высота бортов — 50 см. В случае пробоя днища, до какого уровня поднимется вода, перед тем как пустая лодка потонет?
До высоты бортов?
Эм, с такой плотностью оно не потонет вообще, у воды плотность выше :)
З.Ы. Под «потонет» я понимаю «верхняя точка лодки ниже уровня воды»
З.Ы. Под «потонет» я понимаю «верхняя точка лодки ниже уровня воды»
*не туда*
После окончания олимпиады, нам прислали результаты и официальное решение каждой задачи. Я может плохо запомнил само условие задачи, но решение я запомнил дословно — «Дерево в воде не тонет».
Мы долго угорали над нашей невнимательностью и скользкости формулировки задачи, но все участники высчитывали уровень воды, при известной плотности материала лодки. А когда он получался выше борта, то начинали искать «ошибки» в своих расчётах, и некоторые находили ведь :)
Мы долго угорали над нашей невнимательностью и скользкости формулировки задачи, но все участники высчитывали уровень воды, при известной плотности материала лодки. А когда он получался выше борта, то начинали искать «ошибки» в своих расчётах, и некоторые находили ведь :)
Лодка не потонет (не пойдёт ко дну и не оторвётся от поверхности воды). Если под «потонет» понимать, что уровень воды в лодке и снаружи от лодки выровняется, и допустить, что лодка — это короб без крышки с равной толщиной стенок и днища, то решение будет таким:
Пусть x м — уровень воды в лодке. Пусть d м — толщина стенок. Предположим, что дниже полностью ушло под воду. Тогда объем вытесненной воды равен 3d + 8xd. 8 — это суммарная длина бортов. Масса вытесненной воды 1000 (3d + 8xd).
Общий объем лодки 3d + 0.5 * 8d. Общая масса лодки 750 (3d + 0.5 * 8d).
1000 (3d + 8xd) = 750 (3d + 0.5 * 8d).
Решаем уравнение, x = 0.28125 (м).
Пусть x м — уровень воды в лодке. Пусть d м — толщина стенок. Предположим, что дниже полностью ушло под воду. Тогда объем вытесненной воды равен 3d + 8xd. 8 — это суммарная длина бортов. Масса вытесненной воды 1000 (3d + 8xd).
Общий объем лодки 3d + 0.5 * 8d. Общая масса лодки 750 (3d + 0.5 * 8d).
1000 (3d + 8xd) = 750 (3d + 0.5 * 8d).
Решаем уравнение, x = 0.28125 (м).
del
В 10-ой задаче последнему мудрецу достаточно вычислить количество колпаков одного цвета и дать бинарный ответ — чётное это число или нечётное.
Решение в статье строится на том же принципе.
В маткружке как-то разбирали обобщённое решение этой задачи для колпаков разных цветов — трёх и более. К сожалению, решение не отложилось в памяти. :-(
Хорошее расширение задачи про колпаки. В решении, приведенном в статье, складывают по модулю 2. Если цветов колпаков N, то расчёты нужно вести по модулю N, причем тут уже будет разница, где складывать, а где вычитать. Цвета впереди стоящих нужно складывать, а произнесенные цвета вычитать.
Точно! Сообразил.
Допустим, используются чёрные, белые и красные колпаки, которые у нас будут обозначены как 0, 1 и 2.
Тогда последний мудрец просчитывает сумму всех видимых ему колпаков, вычисляет остаток от деления на 3 и называет цвет, соответствующий этому остатку.
Б --> К --> Ч --> Б --> Б --> Ч даст 1 (4 % 3).
Тот, кто находится перед ним, по разнице в остатках (между произнесённым и видимыми впереди) может определить свой цвет.
Он видит 2, значит, на нём красный колпак: 2 + 2 = 1 (mod 3)
Спасибо вам!
Допустим, используются чёрные, белые и красные колпаки, которые у нас будут обозначены как 0, 1 и 2.
Тогда последний мудрец просчитывает сумму всех видимых ему колпаков, вычисляет остаток от деления на 3 и называет цвет, соответствующий этому остатку.
Б --> К --> Ч --> Б --> Б --> Ч даст 1 (4 % 3).
Тот, кто находится перед ним, по разнице в остатках (между произнесённым и видимыми впереди) может определить свой цвет.
Он видит 2, значит, на нём красный колпак: 2 + 2 = 1 (mod 3)
Спасибо вам!
В одном варианте 10й задачи количество мудрецов бесконечное, нужно придумать алгоритм действий, чтобы число неправильных ответов было конечно. Самое веселое, что в таком решении мудрецам даже необязательно слышать, что говорят предыдущие. Но у решения есть небольшой нюанс ;)
6я задача ещё напрямую следует из малой теоремы Ферма
Поясните подробнее, пожалуйста.
Малая теорема Ферма: a^p == a (mod p).
(n + 1)^p — n^p — 1 == n + 1 — n — 1 == 0 (mod p) — значит делится нацело на p.
(n + 1)^p — n^p — 1 == n + 1 — n — 1 == 0 (mod p) — значит делится нацело на p.
У меня в школе на олимпиаде задача про муху была. Я честно подсчитал скорость, записал ее в ответе… а потом меня обломали и сказали, что правильный ответ — мухи с такой скоростью не летают :-(
Дополню:
1. Каждое утро монах несет воду в монастырь на вершине горы. Путь долгий и приходит он только к вечеру. На следующий день он спускается. По пути он когда хочет останавливается передохнуть и вниз он обычно идет быстрее чем наверх. Требуется доказать, что на дороге к монастырю всегда будет точка, которую он проходит в одно и то же время дня при подъеме и спуске.
2. (для программистов) Имеется 100 мешков с монетами, причем известно, что в одном мешке все монеты фальшивые, они на 1 грамм легче настоящих. Как за 1 взвешивание определить в каком мешке фальшивки?
1. Каждое утро монах несет воду в монастырь на вершине горы. Путь долгий и приходит он только к вечеру. На следующий день он спускается. По пути он когда хочет останавливается передохнуть и вниз он обычно идет быстрее чем наверх. Требуется доказать, что на дороге к монастырю всегда будет точка, которую он проходит в одно и то же время дня при подъеме и спуске.
2. (для программистов) Имеется 100 мешков с монетами, причем известно, что в одном мешке все монеты фальшивые, они на 1 грамм легче настоящих. Как за 1 взвешивание определить в каком мешке фальшивки?
Решение
1. Пусть высота горы равна 1. Построим зависимость высоты монаха над основанием горы от времени. Когда он поднимается, получаем непрерывную неубывающую функцию, когда спускается — непрерывная невозрастающая функция. В начальный момент времени функция подъема имеет значение 0, функция спуска 1, в конечный момент — наоборот.
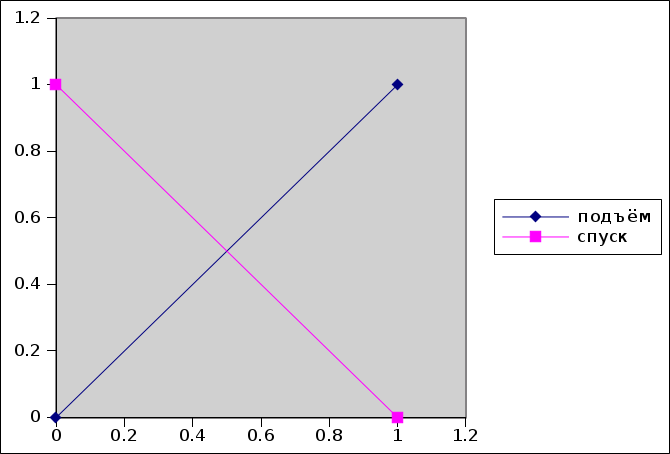
Вычтем из неубывающей функции невозрастающую. Получается неубывающая непрерывная функция, проходящая значения от -1 до 1. Помнится, в матанализе была теорема, согласно которой такая функция где-то на отрезке, где всё это выполняется, принимает значение 0. Там функция подъема пересекается с функцией спуска, то есть монах находится на одной высоте в одно время.
2. Дольше всего до меня доходило, что взвешивание — это определение веса, а не сравнение весов. Кроме того, я сделал допущение, что нам известен вес правильной монетки, а не только разница в весе с фальшивкой.
Берем из первого мешка одну монетку, из второго две, из третьего три и так далее. Все их кладем на весы и узнаем вес. Считаем, сколько должно было бы получиться, если бы все монеты были правильными (вес правильной монеты * число монет). Вычитаем из этого числа то, что показали весы. Это и будет номер мешка с подделками, так как он дал вклад в уменьшение веса, равный числу использованных монет, то есть своему номеру.

Вычтем из неубывающей функции невозрастающую. Получается неубывающая непрерывная функция, проходящая значения от -1 до 1. Помнится, в матанализе была теорема, согласно которой такая функция где-то на отрезке, где всё это выполняется, принимает значение 0. Там функция подъема пересекается с функцией спуска, то есть монах находится на одной высоте в одно время.

2. Дольше всего до меня доходило, что взвешивание — это определение веса, а не сравнение весов. Кроме того, я сделал допущение, что нам известен вес правильной монетки, а не только разница в весе с фальшивкой.
Берем из первого мешка одну монетку, из второго две, из третьего три и так далее. Все их кладем на весы и узнаем вес. Считаем, сколько должно было бы получиться, если бы все монеты были правильными (вес правильной монеты * число монет). Вычитаем из этого числа то, что показали весы. Это и будет номер мешка с подделками, так как он дал вклад в уменьшение веса, равный числу использованных монет, то есть своему номеру.
решение 2
>Дольше всего до меня доходило, что взвешивание — это определение веса, а не сравнение весов.
Со сравнением весов тоже можно — просто берем вначале из первых 50 мешков на одну чашу, и из других 50 на другую, а дальше логика схожа.
Тогда нам не нужен реальный вес, а нужна как раз разница. Увидев эту разницу в весе двух куч монеток, мы узнаем порядковый номер мешка, ну а то куда клонятся весы покажет правильную часть мешков.
Со сравнением весов тоже можно — просто берем вначале из первых 50 мешков на одну чашу, и из других 50 на другую, а дальше логика схожа.
Тогда нам не нужен реальный вес, а нужна как раз разница. Увидев эту разницу в весе двух куч монеток, мы узнаем порядковый номер мешка, ну а то куда клонятся весы покажет правильную часть мешков.
Комментарий
Браво! Ваше решение лучше, так как для него не требуется знание веса правильной монетки, ведь эти веса компенсируются справа и слева.
Хотя в первом комментарии я под сравнением понимал только куда клонится стрелка (>, =, <), без разницы. Имея в арсенале только такое сравнение, задачу не решить за одно взвешивание.
Хотя в первом комментарии я под сравнением понимал только куда клонится стрелка (>, =, <), без разницы. Имея в арсенале только такое сравнение, задачу не решить за одно взвешивание.
Отлично! Чуть ниже решение первой задачи, а пока — продолжаем: На краю пропасти за ветку куста зацепиласть паутинка с повисшим на ней пауком. Паутинка растягивается, паук лезет наверх. За минуту паук проползает 1см, паутинка растягивается на 5см. Общая стартовая длина — 1м. Все эти величины, в общем, не важны, требуется ответ на вопрос — доберется ли когда-нибудь паук до верха, при условии, что живет он вечно, паутинка не рвется, а пропасть имеет бесконечную глубину? Причем требуется именно простой ответ, в духе даосских монахов не знающих математики.
Ответ: доберется. Простого доказательства я не придумал. Под спойлером доказательство того, что доля оставшегося пути всё время уменьшается и не выходит на плато.
Интересно после этого услышать простое доказательство без использования сложной математики.
Доказательство
Пусть s — оставшийся путь паука, в метрах, l — общая длина паутины, в метрах, v1 — скорость паука, v2 — скорость увеличения паутины.
Доля оставшегося пути равна s/l. На следующем шаге пауку останется пройти s — v1 + s/l * v2, а длина паутины будет l + v2.
Сравним s/l и s — v1 + s/l * v2.
Домножим обе части сравнения на положительное число l * (l+v2).
Получим сравнение sl + s*v2 и sl — v1*l + s * v2.
Сократим. Получим слева 0, справа -v1*l. Значит s/l > s — v1 + s/l * v2, то есть доля оставшегося пути постоянно убывает.
Разделим -v1*l обратно на l * (l+v2) и получим v1/(l+v2), которое убывает как гипербола, следовательно его первообразная (доля оставшегося пути) ведет себя как логарифм, то есть не выходит на плато.
Доля оставшегося пути равна s/l. На следующем шаге пауку останется пройти s — v1 + s/l * v2, а длина паутины будет l + v2.
Сравним s/l и s — v1 + s/l * v2.
Домножим обе части сравнения на положительное число l * (l+v2).
Получим сравнение sl + s*v2 и sl — v1*l + s * v2.
Сократим. Получим слева 0, справа -v1*l. Значит s/l > s — v1 + s/l * v2, то есть доля оставшегося пути постоянно убывает.
Разделим -v1*l обратно на l * (l+v2) и получим v1/(l+v2), которое убывает как гипербола, следовательно его первообразная (доля оставшегося пути) ведет себя как логарифм, то есть не выходит на плато.
Интересно после этого услышать простое доказательство без использования сложной математики.
Откуда взялась s/l*v2?
В общем случае задача сводится к задаче исчерпания одного бесконечного множества другим. В рамках теории множеств — исчерпает, в рамках интуиционизма — нет.
В общем случае задача сводится к задаче исчерпания одного бесконечного множества другим. В рамках теории множеств — исчерпает, в рамках интуиционизма — нет.
s/l — доля оставшегося пути. Всего паутина вырастает на v2, а на её часть, расположенную выше паука, приходится часть s/l от общего роста. Итого s/l * v2.
В условии сказано: паук прополз 1 см, паутина удлинилась НА 5 см.
Правильно, а кусок паутины, расположенный выше паука, удлиннился на s/l * 5см. Считаем, что паутина удлинняется равномерно по всей длине. s/l — доля этого куска паутины во всей паутине.
Да, я такой вариант не рассматривал. Но что, если паутинка растягивается под весом паука?
Если паутинка растягивается под весом паука, то растягиваться на 5 см будет только та её часть, которая над пауком. Тогда паук будет за ход подниматься на 1 см и опускаться на 5 см и, очевидно, никогда не доберется до вершины.
А вот и нет. В условиях стоит слово бесконечность. И вот при переходе в бесконечность мы с удивлением обнаруживаем, что длина пути, пройденного пауком и длина паутинки равны. Однако тут есть момент, мы делали бесконечный переход, опираясь на теорию множеств, в интуиционизме это не так.
Слово «очевидно» тут очень подозрительно выглядит. Насколько я помню, в оригинале задачи как раз и было сказано, что паутина растягивается под весом паука, так что ваше решение не совсем верно. Моя вина — неточно поставил условие.
Насколько я помню эта задача была в разделе про ценность попыток достичь цели в условиях, когда достижение её «очевидно» бессмысленно, т.е. непрерывные усилия перебарывают кажущуюся очевидность. Это означает, что данная задача должна иметь положительное решение «очевидное» для даоса :) Видимо я пока не достиг. А в книге решения не было.
Насколько я помню эта задача была в разделе про ценность попыток достичь цели в условиях, когда достижение её «очевидно» бессмысленно, т.е. непрерывные усилия перебарывают кажущуюся очевидность. Это означает, что данная задача должна иметь положительное решение «очевидное» для даоса :) Видимо я пока не достиг. А в книге решения не было.
Если бы я знал! Оно как дао ходит вокруг и никак не дается. Я её решал еще более худшим образом (как настоящий программист): я составил вечный цикл с единственным условием выхода — достижение верха с точностью 1 см. Оно и посчитало… И я очень надеялся, что кто-то тут найдет простое решение.
Предлагаю еще немного разнообралить задачу — каждые 20 секунд паук чихает, при этом выделяется 0.0001 л воздуха, при направлении чиха строго против растягивания паутины. Требуется определить среднее отклонение скорости растяжения нити в различные сезоны года если вычих воздуха происходит со скоростью 0.0001 м/с?
Браво! Вторая задача с поправками bogolt — совершенно точно. А вот первая ;) нет. Это реальная задача из даосских то ли сказок, то ли анекдотов, у них не всегда поймешь. Монахи не знали математики, их решение было следующим: какая разница, в какой день пойдет монах? Сегодня он пошел наверх, а второй он, сегодня же, пошел вниз. У них ведь одна дорога на двоих, значит они точно встретятся. Напоминаю, после решения должно наступать просветление.
Еще немного в тему парадоксов: 4 задачки из книги The Art Of Thinking Clearly.
Про эти 4 задачки в книге
Парадокс этих задач в том, что самый очевидный ответ является неверным. По статистике 60% людей отвечают на эти вопросы неправильно, хотя по сложности они едва ли сложнее задач 5го класса.
Задача 2.
Длину стороны CB обозначим H, Длину СМ (и АМ) обозначим L
Угол САВ обозначим «a», угол ABM — «b».
Нужно доказать a>b.
Ход решения.
Поигравшись с суммами углов треугольников получаем, что угол CMB равен a+b.
Его тангенс: tg(a+b) = H/L.
С другой стороны, tg(a) = H/(2*L).
Следовательно, tg(a+b) = 2*tg(a).
0<a+b<pi/2, в этом диапазоне производная тангенса больше 1, значит tg(a+b) > 2*tg((a+b)/2).
Получаем: 2*tg((a+b)/2) < 2*tg(a) => (a+b)/2 < a => a>b.
Длину стороны CB обозначим H, Длину СМ (и АМ) обозначим L
Угол САВ обозначим «a», угол ABM — «b».
Нужно доказать a>b.
Ход решения.
Поигравшись с суммами углов треугольников получаем, что угол CMB равен a+b.
Его тангенс: tg(a+b) = H/L.
С другой стороны, tg(a) = H/(2*L).
Следовательно, tg(a+b) = 2*tg(a).
0<a+b<pi/2, в этом диапазоне производная тангенса больше 1, значит tg(a+b) > 2*tg((a+b)/2).
Получаем: 2*tg((a+b)/2) < 2*tg(a) => (a+b)/2 < a => a>b.
В копилку задачек можно добавить ту, что про бессмертных эльфов в тюряге, как-то мелькала на хабре.
Вот она: habrahabr.ru/post/69558/
Про первую задачу, возможно и легенда, но много упоминаний видел:
Один из выдающихся математиков современности, Джон фон Нейман, когда ему задали эту задачу, задумался лишь на миг и сказал: «Ну, конечно, 200 км!» Приятель спросил его: «Как вам удалось так быстро получить ответ?» «Я просуммировал ряд», — ответил математик.
Один из выдающихся математиков современности, Джон фон Нейман, когда ему задали эту задачу, задумался лишь на миг и сказал: «Ну, конечно, 200 км!» Приятель спросил его: «Как вам удалось так быстро получить ответ?» «Я просуммировал ряд», — ответил математик.
К задаче про девочек-мальчиков хочется продолжение:
Можно ли придумать стратегию, при которой соотношение будет получаться отличным от 50/50?
при условии, что вероятность именно 0.5, и не зависит от особенностей пары.
Пример стратегии: продолжать заводить детей до тех пор, пока в семье не будет достигнуто превышение количества мальчиков. Продолжительность жизни считаем конечной.
Можно ли придумать стратегию, при которой соотношение будет получаться отличным от 50/50?
при условии, что вероятность именно 0.5, и не зависит от особенностей пары.
Пример стратегии: продолжать заводить детей до тех пор, пока в семье не будет достигнуто превышение количества мальчиков. Продолжительность жизни считаем конечной.
Если всех детей независимо от пола растят на равных правах, то, кажется, распределение полов сдвинуть не получится. Вроде бы был реальный пример страны, где детей одного пола чаще убивали при помощи абортов, в итоге этого пола стало меньше.
Аборты — это вы уже про какие-то новые времена. Но вообще в прошлом это была обычная практика в некоторых странах.
Сразу вспомнились книги Перельмана. Занимательная физика, алгебра, геометрия и т.д.) Да и вообще, школьные олимпиады :) Первую задачу решал наверное в классе 7-8, точно не вспомню)
Так, например, закон Архимеда нельзя применить к лому, который лежит на дне бассейна.
C чего бы это?
Именно за счёт силы Архимеда лом ПОЛНОСТЬЮ находящийся в воде будет легче, чем на суше.
Извините за путаницу. С одной стороны, сила Архимеда равна нулю, когда погруженное в жидкость тело герметично прижато ко дну. С другой стороны, если плотность тела больше плотности воды, то не применяется правило, согласно которому масса плавающего тела равна массе вытесненной воды. В последнем случае вместо этого применяется аналогичное правило, но сформулированное не для масс, а для объёмов, что важно для решения задачи, а замечание про герметично прилегающее ко дну тело к решению задачи не относится.
Sign up to leave a comment.
10 занимательных задач