 Распространение света в реальном мире это чрезвычайно сложное явление, зависящее от слишком многих факторов, и, располагая ограниченными вычислительными ресурсами, мы не можем себе позволить учитывать в расчетах все нюансы. Поэтому освещение в OpenGL основано на использовании приближенных к реальности упрощенных математических моделей, которые выглядят достаточно похожими, но рассчитываются гораздо проще. Эти модели освещения описывают физику света исходя из нашего понимания его природы. Одна из этих моделей называется моделью освещения по Фонгу (Phong). Модель Фонга состоит из трех главных компонентов: фонового (ambient), рассеянного/диффузного (diffuse) и бликового (specular). Ниже вы можете видеть, что они из себя представляют:
Распространение света в реальном мире это чрезвычайно сложное явление, зависящее от слишком многих факторов, и, располагая ограниченными вычислительными ресурсами, мы не можем себе позволить учитывать в расчетах все нюансы. Поэтому освещение в OpenGL основано на использовании приближенных к реальности упрощенных математических моделей, которые выглядят достаточно похожими, но рассчитываются гораздо проще. Эти модели освещения описывают физику света исходя из нашего понимания его природы. Одна из этих моделей называется моделью освещения по Фонгу (Phong). Модель Фонга состоит из трех главных компонентов: фонового (ambient), рассеянного/диффузного (diffuse) и бликового (specular). Ниже вы можете видеть, что они из себя представляют:

Часть 1
- OpenGL
- Создание окна
- Hello Window
- Hello Triangle
- Shaders
- Текстуры
- Трансформации
- Системы координат
- Камера
Часть 2
- Цвета
- Основы освещения
- Материалы
- Карты освещения
- Источники света
- Множественное освещение
Часть 3
- Фоновое освещение: даже в самой темной сцене обычно всегда есть хоть какой-нибудь свет (луна, дальний свет), поэтому объекты почти никогда не бывают абсолютно чёрными. Чтобы имитировать это, мы используем константу окружающего освещения, которая всегда будет придавать объекту некоторый оттенок.
- Диффузное освещение: имитирует воздействие на объект направленного источника света. Это наиболее визуально значимый компонент модели освещения. Чем большая часть поверхности объекта обращена к источнику света, тем ярче он будет освещен.
- Освещение зеркальных бликов: имитирует яркое пятно света (блик), которое появляется на блестящих объектах. По цвету зеркальные блики часто ближе к цвету источника света, чем к цвету объекта.
Для создания визуально интересных сцен нам нужно смоделировать хотя бы эти 3 составляющих свет компонента. Начнем с самого простого: с фонового освещения.
Фоновое освещение
Свет обычно исходит не от одного, а от многих источников света находящихся вокруг нас, даже если мы их не видим непосредственно. Одним из свойств света является то, что он может рассеиваться и отражаться во многих направлениях, достигая мест, которые не находятся в прямой видимости; таким образом свет может отражаться от разных поверхностей и оказывать косвенное влияние на освещение объекта. Алгоритмы, в которых учитываются эти свойства света, называются алгоритмами глобального освещения, но они трудозатратны и/или сложны.
Поскольку мы не очень любим трудные и ресурсоёмкие алгоритмы, то начнем с использования весьма упрощенной модели глобального освещения, а именно с Фонового освещения. В предыдущем разделе вы видели, как использовался неяркий постоянный цвет, который суммировался с цветом фрагмента объекта, и это создавало впечатление наличия в сцене рассеянного света, хотя прямого источника такого света не было.
Добавить фоновое освещение в сцену очень просто. Для этого нужно взять цвет источника света, умножить его на небольшой константный коэффициент фонового освещения, затем умножить полученное значение на цвет объекта и использовать вычисленную величину как цвет фрагмента:
void main()
{
float ambientStrength = 0.1f;
vec3 ambient = ambientStrength * lightColor;
vec3 result = ambient * objectColor;
color = vec4(result, 1.0f);
}Если вы сейчас запустите программу, то увидите, что на ваш объект успешно наложен первый компонент модели освещения Фонга. Объект довольно темный, но не полностью, поскольку к нему применено фоновое освещение (обратите внимание, что куб лампы не изменился, потому что для его визуализации мы применяем другой шейдер). Сцена должна выглядеть примерно так:
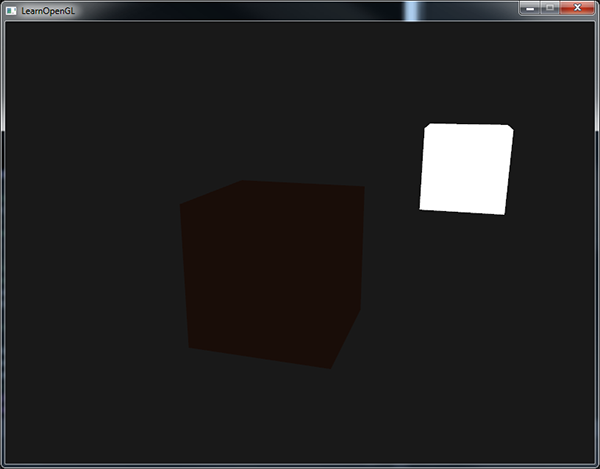
Диффузное освещение
Фоновое освещение само по себе не дает никаких интересных результатов, зато диффузное освещение оказывает на внешний вид объекта весьма значительное визуальное воздействие. Чем более перпендикулярно направлению лучей источника света расположены фрагменты объекта, тем большую яркость им придает диффузная составляющая освещения. Чтобы лучше понять диффузное освещение, взгляните на следующее изображение:
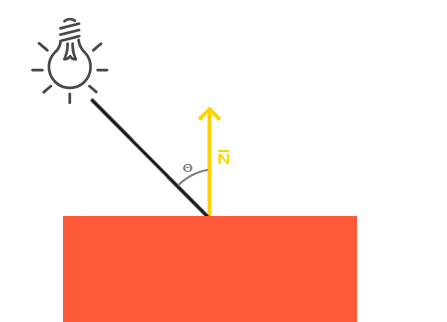
p>Слева мы видим исходящий от источника света луч, направленный на некоторый фрагмент нашего объекта. Нам нужно измерить угол падения луча на фрагмент. Воздействие света источника на цвет фрагмента становится максимальным при перпендикулярном направлении луча к поверхности объекта. Для измерения угла между лучом света и фрагментом мы воспользуемся так называемым вектором нормали, который является перпендикуляром к поверхности фрагмента (вектор нормали изображен в виде желтой стрелки); мы поговорим об этом позже. Тогда угол между двумя векторами можно легко вычислить с помощью скалярного произведения.
Возможно, вы помните из урока по трансформациям, что чем меньше угол между двумя единичными векторами, тем больше результат скалярного произведения стремится к значению 1.0. Когда угол между обоими векторами составляет 90 градусов, скалярное произведение этих векторов становится равным 0. То же самое относится и к углу Θ: чем больше становится Θ, тем меньшее влияние оказывает источник света на цвет фрагмента.
Обратите внимание, что для получения (только) косинуса угла между обоими векторами мы будем работать с единичными векторами (векторами единичной длины), поэтому должны убедиться, что все векторы нормализованы, в противном случае скалярное произведение векторов вернет результат, превышающий значение косинуса (см. урок Трансформации).
Таки образом, возвращаемая в результате скалярного произведения величина, может быть использована для вычисления силы влияния источника света на цвет фрагмента; это приведет к различной освещенности фрагментов, зависящей от их ориентации по отношению к направлению лучей света.
Итак, что нам нужно для расчета диффузного освещения?
- Вектор нормали: вектор, перпендикулярный освещаемой поверхности
- Направленный луч света: вектор направления, который является разностью между позицией источника света и позицией фрагмента. Для вычисления этого луча, нам нужны координата источника света и координата фрагмента.
Вектора нормалей
Вектор нормали — это (единичный) вектор, перпендикулярный поверхности, построенной на данной вершине. Так как вершина сама по себе не имеет поверхности (это всего лишь точка в пространстве), то для нахождения вектора нормали используются соседние вершины. Для вычислении нормалей вершин куба мы можем сделать небольшую хитрость и применить к граням векторное произведение, но поскольку куб по форме представляет собой довольно простую фигуру, то мы добавим нормали к данным вершин вручную. Обновленный массив вершинных данных можно найти здесь. Попытайтесь вообразить нормали в виде векторов, направленных перпендикулярно поверхностям плоскостей куба (куб состоит из 6 плоскостей).
Поскольку мы добавили дополнительные данные в массив вершин, то нам необходимо обновить вершинный шейдер освещения:
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
...Теперь, после добавления каждой вершине вектора нормали и обновления вершинного шейдер, нам также необходимо обновить указатели атрибутов вершин. Обратите внимание, что объект-лампа извлекает данные вершин из этого же самого массива, но вершинный шейдер лампы не использует вновь добавленные вектора нормалей. Нам не нужно обновлять ни шейдеры лампы, ни её атрибуты, но в связи с изменением размера массива вершин, мы должны изменить настройку указателей атрибутов.
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), (GLvoid*)0);
glEnableVertexAttribArray(0);Для каждой вершины мы хотим использовать только первые 3 float-значения, а последние 3 значения пропускать, поэтому нам нужно только обновить параметр шага (stride) до величины, равной 6 размерам переменной типа GLfloat, и все.
Работа с массивом вершин, в котором шейдер использует не все данные, может показаться не неэффективной, но эти данные уже были загружены в память GPU из массива объекта-контейнера, поэтому никаких новых данных нам загружать не нужно. На практике такой подход более эффективен по сравнению с созданием для лампы собственного нового VBO.
Все расчеты освещения выполняются во фрагментном шейдере, поэтому нам нужно перенаправить векторы нормалей из вершинного шейдера во фрагментный шейдер. Давайте это сделаем:
out vec3 Normal;
void main()
{
gl_Position = projection * view * model * vec4(position, 1.0f);
Normal = normal;
} Осталось только объявить соответствующую входную переменную во фрагментном шейдере:
in vec3 Normal;Вычисление диффузного цвета
Теперь у нас для каждой вершины есть вектор нормали, но нам по-прежнему нужны вектора с координатами источника света и фрагмента. Так как позиция источника света задана одной не изменяющейся переменной, то мы просто объявим её во фрагментном шейдере как uniform-переменную:
uniform vec3 lightPos;А затем присвоим ей значение в игровом цикле (или вне его, поскольку значение этой переменной не меняется). В качестве местоположения источника света мы используем объявленный в предыдущем уроке вектор lightPos:
GLint lightPosLoc = glGetUniformLocation(lightingShader.Program, "lightPos");
glUniform3f(lightPosLoc, lightPos.x, lightPos.y, lightPos.z); Последнее, что потребуется, это позиция текущего фрагмента. Мы собираемся производить все расчеты освещения в мировом пространстве координат, поэтому и позиции вершин нам будут нужны нужна в мировых координатах. Преобразование позиции вершины в мировые координаты достигается умножением её атрибута позиции только на матрицу модели (без матриц вида и проекции). Это легко может быть выполнено в вершинном шейдере, поэтому давайте объявим в нем выходную переменную и вычислим координаты вершины в мировом пространств:
out vec3 FragPos;
out vec3 Normal;
void main()
{
gl_Position = projection * view * model * vec4(position, 1.0f);
FragPos = vec3(model * vec4(position, 1.0f));
Normal = normal;
}И, наконец, добавьте соответствующую входную переменную во фрагментный шейдер:
in vec3 FragPos;Теперь, когда все необходимые переменные установлены, мы можем начать во фрагментном шейдере расчеты освещения.
Первое, что нам нужно вычислить, это вектор направления между источником света и фрагментом. Мы уже говорили о том, что этот вектор является разностью позиций источника света и фрагмента. Как вы, возможно, помните из урока по трансформациям, мы можем легко вычислить эту разность, вычитая один вектор из другого. Мы также хотим удостовериться в том, что все интересующие нас вектора будут единичной длины, поэтому мы подвергаем нормализации как полученный при вычитании вектор направления источника света, так и вектор нормали:
vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);При расчете освещения нам обычно не важны ни размеры векторов, ни их местоположение; нас интересуют только направления. Так как значимой характеристикой является только ориентация векторов, то почти все вычисления производятся с векторами единичной длины, поскольку это упрощает большинство расчетов (например, скалярное произведение). Поэтому при выполнении расчетов освещения всегда проверяйте, сделали ли вы нормализацию соответствующих векторов, что бы быть уверенным в том, что они действительно являются единичными. Отсутствие нормализации векторов весьма часто встречающаяся ошибка.
Дальше, посредством скалярного произведения векторов norm и lightDir, нам нужно вычислить величину воздействия диффузного освещения на текущий фрагмент. Затем, это значение умножается на цвет источника света, и в результате мы получим компоненту диффузного освещения, которая будет становиться темнее с ростом угла между векторами:
float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;Если угол между векторами больше 90 градусов, то результат скалярного произведения будет отрицательным, и мы получим отрицательную составляющую диффузного света. По этой причине мы используем функцию max, которая возвращает наибольший из переданных ей параметров, и гарантирует, что диффузная компонента света (и, следовательно, цвета) никогда не будут меньше 0.0. Моделей освещения для отрицательных значений цвета не существует, так что если вы не один из эксцентричных художников, то от отрицательных цветов лучше держаться подальше.
Теперь, когда у нас есть фоновый и диффузный компоненты, мы суммируем их цвета, а затем умножаем результат на цвет объекта, получая таким образом результирующий цвет выходного фрагмента:
vec3 result = (ambient + diffuse) * objectColor;
color = vec4(result, 1.0f);Если ваше приложение (и шейдеры) скомпилированы успешно, вы увидите что-то вроде этого:
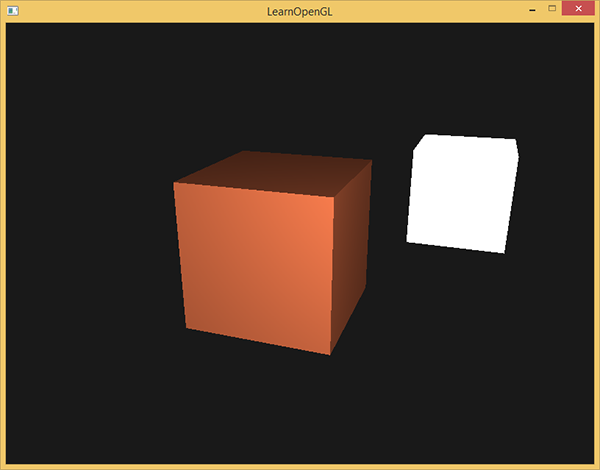
Вместе с компонентой диффузного освещения куб начинает выглядеть более реалистично. Попробуйте мысленно представить себе нормали плоскостей куба, а потом, перемещаясь вокруг него понаблюдать за изменением яркости, и увидеть, что с увеличением угла между нормалью и направлением источника света, фрагменты становятся темнее.
Если у вас возникли сложности, то не стесняйтесь сравнивать свой исходный код с полным исходным кодом и кодом фрагментного шейдера.
Еще кое-что
В настоящее время мы передаем вектора нормалей и вершинного шейдера непосредственно в шейдер фрагментов. Однако вычисления, которые мы производили в шейдере фрагментов, выполнялись в координатах мирового пространства, поэтому не должны ли мы преобразовать в мировые координаты так же и вектора нормалей? Вообще то должны, но сделать это будет не так просто, как умножить вектор на матрицу модели.
Во-первых, вектора нормалей это только направления, и они не представляют собой определенных позиции в пространстве. Кроме того, у нормалей нет гомогенной компоненты (w-компонента положения вершины). Это означает, что производимые перемещения модели не должны влиять на вектора нормалей. Поэтому, если мы хотим умножить нормали на матрицу модели, то должны удалить часть матрицы, отвечающей за перемещения, и взять только левую верхнюю матрицу размером 3x3 (заметьте, мы могли бы установить w-компоненту вектора нормали в 0.0 и умножить его на целую матрицу 4x4, что также устранит воздействие значений сдвигов). Таким образом мы применим к векторам нормалей, только преобразования масштаба и поворота.
Во-вторых, если матрица модели выполняет неравномерное масштабирование, то вершины координаты вершин будут изменены таким образом, что вектор нормали
больше не будет перпендикулярен поверхности, поэтому преобразовывать нормали такими матрицами модели мы тоже не сможем. На следующем рисунке показан эффект, производимый на вектор нормали такой матрицей модели (с неоднородным масштабированием):
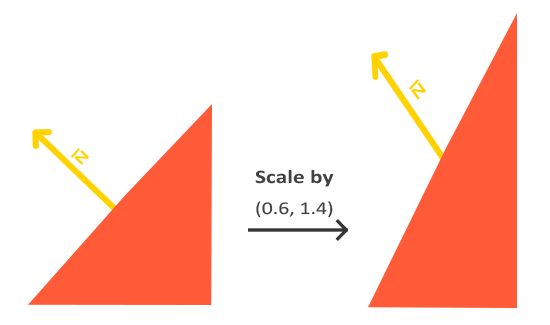
Всякий раз, когда мы применяем неоднородное масштабирование, нормали перестают быть перпендикулярными своим поверхностям, что искажает освещение. (Примечание: однородное масштабирование для нормалей безвредно, так как при этом изменяются направления векторов остаются прежними, а изменяются только их размеры, которые легко корректируются путем нормализации).
Приемом, решающим эту проблему, может служить применение другой матрицы модели, специально предназначенной для векторов нормалей. Эта матрица называется матрицей нормалей, она использует несколько линейных алгебраических операций для устранения эффекта неправильного масштабирования нормалей. Если вы хотите знать, как рассчитывается эта матрица, то предлагаю вам следующую статью.
Матрица нормалей определяется как «транспонированная обратная подматрица 3х3 левого верхнего угла матрицы модели». Уфф, это уже слишком, и если вы не совсем понимаете, что всё это значит, не переживайте; обратные и транспонированные матрицы мы еще не обсуждали. Обратите внимание, что во многих обучающих примерах матрица нормалей вычисляется применением вышеописанных операций к матрице модели-вида, но поскольку мы работаем в мировом пространстве (а не в пространстве вида), то используем только одну матрицу модели.
В вершинном шейдере мы можем создать матрицу нормалей самостоятельно, используя для этого функции обращения и транспонирования, которые работают с любыми типами матриц. Обратите внимание, что мы приводим матрицу к типу 3x3, чтобы гарантировать утрату матрицей своих сдвигающих свойств и обеспечить возможность умножения на вектор нормали типа vec3:
Normal = mat3(transpose(inverse(model))) * normal;В примерах из раздела о рассеянном освещении всё работало корректно потому что мы не производили над объектом никаких операций масштабирования, поэтому не было необходимости использовать матрицу нормалей и можно было просто умножить нормали на матрицу модели. Однако, если вы будете применять неравномерное масштабирование, то умножение вектора нормали именно на матрицу нормалей станет весьма существенным.
Обращение матриц является дорогостоящей операцией даже для шейдеров, поэтому везде, где это возможно, старайтесь избегать выполнения в шейдерах подобных вычислений, тем более что они будут сделаны для каждой вершины вашей сцены. В учебных целях это допустимо, но в прикладных приложениях скорее всего вы предпочтете рассчитывать матрицу нормалей на CPU, и перед визуализацией передавать ее шейдерам с помощью uniform-переменной (также как и матрицу модели).
Освещение зеркальных бликов
Если вы еще не окончательно изнурены всеми этими расчетами освещения, то можем приступить к завершению знакомства с моделью Фонга, добавив последнюю компоненту зеркальных бликов.
Освещение зеркальных бликов, так же как и рассеянное освещение, основано на векторе направления источника света и нормали поверхности объекта, но кроме этого в вычислениях учитывается и позиция наблюдателя, то есть направление, в котором игрок смотрит на фрагмент. Зеркальное освещение основано на отражательных свойствах света. Если представить поверхность объекта в виде зеркала, то освещение бликов будет наибольшим в том месте, где бы мы увидели отраженный от поверхности свет источника. Этот эффект показан на следующем изображении:
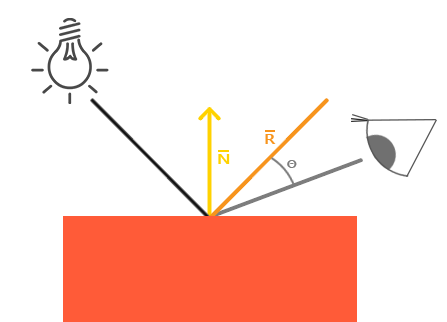
Вектор отражения вычисляется путем отражения направления света относительно вектора нормали. Затем мы вычисляем угловое расстояние между этим вектором отражения и направлением взгляда; чем меньше угол между ними, тем большее воздействие на цвет фрагмента оказывает освещение зеркальных бликов. В результате этого эффекта, когда мы смотрим в направлении источника света, то видим на поверхности объекта отраженный блик.
Вектор просмотра — это еще одна дополнительная переменная, необходимая для рассчета освещения зеркальных бликов. Мы можем её вычислить используя мировые координаты точки зрения наблюдателя и положения фрагмента. Затем мы вычисляем интенсивность блика, умножаем ее на цвет освещения и добавляем к вычисленным ранее компонентам фонового и рассеянного освещения.
Мы решили производить расчеты освещения в мировом пространстве, но большинство людей предпочитают это делать в пространстве вида. Преимущество рассчетов освещения в координатах вида заключается в том, что позиция наблюдателя всегда находится в (0,0,0), и вычислять её не нужно. Тем не менее, я считаю, что вычисление освещения в мировых координатах в учебных целях более понятно. Если вы всё же хотите рассчитать освещенность в пространстве вида,
то вам нужно умножать все соответствующие вектора на матрицу вида (не забудьте также изменить и матрицу нормалей).
Чтобы получить координаты наблюдателя в мировом пространстве, мы просто берем вектор положения объекта камеры (которая, разумеется, и является наблюдателем). Так что давайте добавим еще одну uniform-переменную в шейдер фрагментов и передадим в него соответствующий вектор положения камеры:
uniform vec3 viewPos;GLint viewPosLoc = glGetUniformLocation(lightingShader.Program, "viewPos");
glUniform3f(viewPosLoc, camera.Position.x, camera.Position.y, camera.Position.z);Теперь, когда у нас есть все необходимые переменные, мы можем вычислить интенсивность блика. Для начала мы зададим зеркальному блику среднее значение интенсивности, чтобы он не оказывал слишком сильного воздействия:
float specularStrength = 0.5f;Если бы мы установили значение этой переменной в 1.0f, то получили бы очень яркий компонент зеркального блика, который для кораллового куба был бы чрезмерным. О правильной настройке всех этих интенсивностей освещения и о том, как они влияют на объекты мы поговорим в следующем уроке. А пока вычислим вектор направления взгляда и соответствующий ему вектор отражения относительно оси, которой является нормаль:
vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);Обратите внимание, что мы инвертировали вектор lightDir. Функция reflect ожидает, что первый вектор будет указывать направление от источника света к положению фрагмента, но вектор lightDir в настоящее время указывает в обратную сторону, то есть от фрагмента к источнику света (направление зависит от порядка вычитания векторов, которое мы делали при вычислении вектора lightDir). Поэтому, для получения правильного вектора отражения, мы меняем его направление на противоположное посредством инверсии вектора lightDir. Предполагается, что второй аргумент должен быть единичной длинны, и мы передаем нормализованный вектор norm.
Остается только вычислить компонент зеркального блика. Это выполняется по следующей формуле:
float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;Сначала вычисляется скалярное произведение векторов отражения и направления взгляда (с отсевом отрицательных значений), а затем результат возводится в 32-ю степень. Константное значение 32 задает силу блеска. Чем больше это значение, тем сильнее свет будет отражаться, а не рассеиваться, и тем меньше станет размер пятна блика. Ниже вы можете видеть изображение, демонстрирующее воздействие различных значений блеска на внешний вид объекта:

Мы не хотим, чтобы компонент зеркальных бликов слишком выделялся, поэтому оставим показатель степени равным 32. Остается только сложить полученную величину вместе с компонентами фонового и рассеянного освещения, после чего умножить результат на цвет объекта:
vec3 result = (ambient + diffuse + specular) * objectColor;
color = vec4(result, 1.0f);Теперь мы рассчитали все компоненты освещения модели освещения Фонга. С положения вашей точки зрения вы должны увидеть что-то вроде этого:

Здесь вы можете найти полный исходный код приложения, а тут вершинный и фрагментный шейдеры.
В те времена, когда щейдеры еще только начали появляться, разработчики проводили вычисления освещения по модели Фонга в вершинном шейдере. Преимущество такого подхода заключалось в его большей производительности, так как обычно вершин гораздо меньше, чем фрагментов, и поэтому (дорогие) расчеты освещения выполняются реже. Однако вычисленное в вершинном шейдере значение цвета является точным только для этой вершины, а цвета окружающих её фрагментов получают путем интерполяции освещения соседних вершин. Поэтому, если не использовалось большое количество вершин, то освещение было не очень реалистичным:
Если модель освещения Фонга реализована в вершинном шейдере, то она называется методом тонирования Гуро, а не Фонга. Обратите внимание, что из-за интерполяции освещение выглядит несколько шероховатым. Как видите, модель Фонга дает более сглаженные результаты освещения.
К настоящему моменту вы должны начать понимать, насколько мощными средствами являются шейдеры. С небольшими количеством входных данных при помощи шейдеров можно рассчитать освещение всех объектов сцены. В следующих уроках мы углубимся в те возможности, которые предоставляет эта модель освещения.
Упражнения
- Сейчас наш источник света это скучная неподвижная лампа. Сделайте его движущимся вокруг сцены, используя функции sin или cos. Наблюдение за изменением освещения даст вам хорошее представление о модели Фонга: решение.
- Попробуйте менять в модели освещения силы воздействия фоновой, рассеянной и зеркальной компонент, и посмотрите, как это отразится на результате. Также поэкспериментируйте с коэффициентом блеска. Попытайтесь понять, почему определенные значения дают соответствующие им визуальные эффекты.
- Рассчитайте освещение по Фонгу в пространстве вида, а не в мировом: решение.
- Реализуйте освещение методом Гуро, а не Фонга. Если вы все сделали правильно, то освещение куба должно выглядеть не совсем хорошо (особенно зеркальные блики). Объясните, почему у куба такой странный вид: решение.
