
В 1850 году преподобный Томас Киркман, британский математик и настоятель прихода в Ланкашире, сформулировал невинно выглядящую головоломку в развлекательном журнале для любителей математики «Записная книжка леди и джентльменов»:
«Пятнадцать юных школьниц выходят на прогулку семь дней рядами по трое: нужно каждый день располагать их так, чтобы одна и та же пара школьниц никогда не встречалась дважды в одном ряду».
Задачка выглядит простой, но если попробовать её решить, то сразу понимаешь, что это не так. Можете попробовать решить её с карандашом и бумагой или сыграть в HTML-версию.
В силу своей ложной простоты задача быстро стала знаменитой. Свои решения присылали любители математики, а учёные публиковали научные статьи с попыткой сформулировать общее решение для проблемы.
В результате, эта головоломка помогла сформировать новое направление математики: комбинаторные схемы, которому сейчас посвящены толстые учебники. Что началось как простая задачка по распределению людей по группам (или схемам, как в итоге их назвали), теперь стало методом, который применяется в экспериментальном дизайне, кодах коррекции ошибок в информатике, криптографии, сельском хозяйстве, спорте и даже в мошенничествах с азартными играми (была история, когда преступный картель заработал миллионы долларов за семь лет, скупая билеты со всеми возможными комбинациями 5 из 46 в лотерее 6 из 46, если стоимость билетов была ниже, чем дополнительные бонусы за выигрыш 5 из 46 плюс вероятность выигрыша джекпота).
Например, классический код Хамминга для коррекции ошибок использует решение задачи про школьниц (создание групп из трёх школьниц, где ни одна пара не повторяется), но только для схемы из семи девушек (бит).
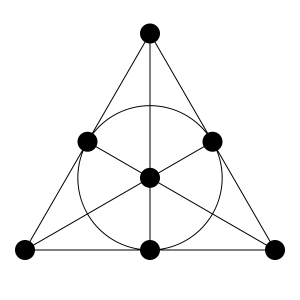
Плоскость Фано для (7, 3, 2)
Удивительнее всего, что за 165 лет математики так и не смогли решить задачу в общем виде. Они так и не могут дать ответ, каково решение у головоломки при начальных условиях: есть n школьниц, нужно создать группы размером k, так что наборы из t девушек никогда не встречались дважды в одной группе. Такая формулировка называется схемой (n, k, t).
Например, для группы из 19 девушек существует более 11 миллиардов возможных триплетов, в которых каждая пара встречается только однажды. Это число и является ответом. Но количество вариантов растёт экспоненциально при увеличении количества школьниц.
Понятно, что задача решается при некоторых условиях и не решается при некоторых других. Например, если из шести школьниц составить триплеты из всех возможных пар, то задача очевидно не решается (со школьницей Аней существует пять возможных пар, в то же время в каждом триплете есть две пары с Аней, а пять не делится на два). То есть по принципу делимости сразу отсеивается много вариантов (n, k, t).
В то же время есть (n, k, t), которые вполне соответствуют принципу делимости, но всё равно не имеют решения: например, (47, 3, 2).
За минувшие годы решение стало известно для многих сочетаний (n, k, t), которые были проверены алгебраически или перебором на компьютерах. Но как решить это в общем виде, что делать с исключениями типа (47, 3, 2)? Как понять, имеет задача решение или нет?
Эта задача долгое время считалась одной из самых знаменитых проблем в комбинаторике, говорит математик Джил Калай (Gil Kalai) из Еврейского университета в Иерусалиме в интервью Wired. Он вспоминает, как спорил по этому поводу с коллегами полтора года назад, и они пришли к выводу, что «мы никогда не узнаем ответ, потому что задача явно слишком сложная».
Однако всего через две недели юный профессор математики Питер Киваш (Peter Keevash) из Оксфорда доказал, что Калай не прав. В научной статье от января 2014 года он доказывает, что решение задачи почти всегда существует, если выполняется условие делимости. В новой работе от апреля 2015 года он показал, как подсчитать примерное количество решений для заданных параметров.
Никто не ожидал, что к решению задачи можно применить теорию вероятности, но метод отлично сработал.
Возвращаясь к лотереям, мошенники поняли, что можно сократить количество покупаемых билетов, если скупить все комбинации 5 из 46 (при указании 6 из 46 чисел), тогда они получат абсолютно все дополнительные призы, а могут ещё получить и джекпот. Хотя схема (46, 6, 5) пока не рассчитана, но есть схемы, достаточно близкие для практического применения. Одну из них, вероятно, использовал преступный картель.
Количество новых рассчитанных схем постоянно растёт. Многие из них находят практическое применение, как (15, 3, 2) из классической задачи, и (46, 6, 5). Выходят 1000-страничные справочники со схемами. Тем не менее, математики до сих пор теряются в догадках, как определить, существует ли решение для конкретных заданных условий. Благодаря Кивашу мы узнали, что вероятность этого достаточно высока. Так что хотя бы теперь ясно, что при всех неизвестных лучше искать решение, чем отказываться от него. Тем более, существуют инструменты для генерации примерных схем для любых параметров.
Но благодаря работам Киваша появилась надежда, что можно разработать метод для создания точных схем для любых параметров. Если это произойдёт, то станет экстраординарным прорывом в математике.
Впрочем, работа Киваша чисто теоретическая. Специалисты говорят, что создание практических алгоритмов на основе его метода потребует упорного труда ещё нескольких поколений математиков.