В предыдущих статьях мы применили Байесовские сети доверия (БСД) для анализа решений инвестора по опциону колл на акции, затем по самой акции. Далее рассмотрели пример с более развитой версией БСД – диаграммой влияния, которая дополнена узлами решений и полезностей. Сегодня усложним задачу, и построим небольшую диаграмму влияния для анализа арбитражных возможностей при создании синтетической позиции по акции.
В архиве ХАБРа имеются очень качественные материалы Технологического Центра Дойче Банка, в которых детально раскрыты понятия паритета европейских опционов, и арбитражного подхода в финансовой инженерии. Эти материалы помогут нам существенно сократить вводную часть.
Итак, речь пойдет о синтетических финансовых инструментах. Так условно называют инструменты, составленные (синтезированные) из других инструментов. По сути, каждый синтетический инструмент представляет собой портфель инструментов, обладающий собственными параметрами риска и доходности. Характеристики синтетического финансового инструмента (портфеля) можно специально «подогнать», или подобрать так, что они будут копировать характеристики какого-либо другого инструмента. Тогда синтетический инструмент бу��ет давать такой же финансовый результат, как и реплицируемый инструмент, но этот результат будет получен другими средствами. Для чего это нужно?
Использование синтетических инструментов обосновано различными вескими причинами. Например, на рынке может отсутствовать финансовый инструмент, интересующий инвестора. Хорошо известен классический пример: на Чикагской бирже опционов в 1973 г. первоначально были открыты торги только опционами колл на акции, поэтому инвесторы, которым были нужны опционы пут, могли получить их только синтетическим путем [2].
Еще более интересны случаи, когда синтетические позиции позволяют инвесторам извлекать арбитражную прибыль. Такое бывает возможно, если стоимость финансового инструмента в конкретных периодах времени расходится со стоимостью его синтетического аналога. На практике хорошо отработаны алгоритмы создания синтетических инструментов с использованием фундаментальной зависимости между премиями опционов колл и пут на одни и те же акции с одинаковой ценой исполнения и сроком истечения. При непрерывном начислении процента эта зависимость выглядит следующим образом:
Это же выражение при обычном дисконтировании выглядит так:
Здесь С – стоимость опциона колл; Р – стоимость опциона пут; S – стоимость акции; Х – цена исполнения опционов; r – безрисковая ставка процента, Т – срок действия опционов. Теорема паритета европейских опционов достаточно строго доказана и описана в литературе по финансовой инженерии, но главное – формула паритета позволяет при известной стоимости опциона колл найти стоимость опциона пут, и наоборот. Используя формулу паритета европейских опционов, конструируют и анализируют синтетические позиции, построенные с использованием опционов, акций и заемных (наличных) средств. Например, если переписать базовую формулу в следующей последовательности:
то, по сути, мы получим готовый наглядный алгоритм конструирования синтетической акции. Знаки в выражении говорят нам о том, что нужно сделать с конкретными инструментами: купить, продать или занять. В частности, мы видим, что для синтеза акции (S) с использованием опционов нужно купить опцион колл, продать пут, и иметь сумму денег, равную дисконтированной стоимости цены исполнения опционов.
Для того чтобы реализовать возможности формулы паритета опционов, в следующем примере построим модель принятия решений опытным инвестором, который сравнивает две альтернативы:
- купить акцию;
- сформировать синтетическую позицию, аналогичную этой же акции.
Инвестору известно, что при наличии арбитражных возможностей на фондовом рынке он сможет получить дополнительный доход. Предположим, что у инвестора имеются в наличии 100 руб., при этом стоимость европейского трехмесячного опциона колл на акцию на рынке составляет 3 руб., а опциона пут 0,56 руб. Цена исполнения опционов составляет 100 руб., текущий (спот) курс акции равен 100 руб., ставка без риска равна 10 % годовых [1].
На основе анализа состояния рынка акций и собственного опыта инвестор считает, что к моменту формирования синтетической позиции цена акции спот с вероятностью 20% может быть равна 101 руб., и с вероятностью 30% может составлять 99 руб. С учетом этих и других ожиданий он строит следующую диаграмму влияния (Рис. 1).
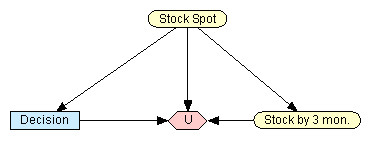
Диаграмма состоит из четырех узлов:
- родительский узел случайной переменной цены акции спот;
- узел случайной переменной цены акции в момент исполнения опционов, т.е. через три месяца;
- узел решений, представляющий два альтернативных варианта решения: Stock (d1) – купить акцию; Synthetic (d2) – сформировать синтетическую позицию, аналогичную этой акции;
- узел полезности U, представляющий ожидаемые результаты инвестирования.
Как и в предыдущих примерах, сеть строится в программе Netica. Для начала поясним некоторые связи на диаграмме. Связь, направленная от узла цены акции спот к узлу цены акции в момент исполнения опционов говорит о том, что наличие арбитражной возможности в любом направлении может повлиять на цену данной акции. Связь, направленная от узла цены акции спот к узлу решений говорит о том, что наличие или отсутствие арбитражных возможностей может повлиять на принятие решения инвестором.
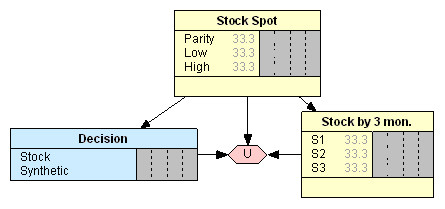
До инициализации модели машина заполняет таблицы равными вероятностями состояний (Рис. 2). Для того чтобы модель заработала, необходимо заполнить все таблицы условных и безусловных вероятностей. Узел цены акции спот является родительским, поэтому таблицу безусловных вероятностей (ТБВ, Таблица 1) его состояния заполняем исходя из арбитражных ожиданий инвестора. В частности, мы уже отметили, что он ожидает цену спот выше цены, соответствующей состоянию паритета опционов (High) с вероятностью 20%, ниже паритета (Low) 30%, а самого паритета с вероятностью 50%.
Таблица 1. ТБВ для узла цены акции спот.
№ | Состояние цены акции | Вероятность, % |
1 | Parity | 50 |
2 | Low | 30 |
3 | High | 20 |
Узел цены акции через три месяца является зависимым, поэтому для него необходимо составить таблицу условных вероятностей (ТУВ, Таблица 2). Здесь инвестор исходит из того, что если арбитражные возможности на рынке отсутствуют, то спрос арбитражеров на данную акцию не изменится, поэтому ее курс с равной вероятностью может принять любое значение (1-я строка ТУВ). Если цена акции спот снизится относительно состояния паритета, что приведет к возможности арбитража, то спрос инвесторов на данную акцию может увеличиться, и ее курс вырастет (2-я строка ТУВ). Наконец, если цена акции спот повысится относительно состояния паритета, то акция будет нужна арбитражерам для продажи, что может привести к снижению ее курса (3-я строка ТУВ).
Таблица 2. ТУВ для узла цены акции через 3 месяца.
№ | Цена акции спот | Цена акции через 3 месяца, % | ||
S1=104 | S2=100 | S3=96 | ||
1 | Parity | 33,33 | 33,33 | 33,34 |
2 | Low | 40 | 30 | 30 |
3 | High | 30 | 30 | 40 |
В таблице полезности необходимо представить все ожидаемые доходы (убытки), которые могут быть получены как по обычной акции, так и по синтетической позиции (Таблица 3). В случае покупки обычной акции (все варианты решения d1) получение дохода возможно, если курс акции к моменту исполнения опционов достигнет уровня S1 (104 руб.); при курсе S2 (100 руб.) инвестор не получает ничего и при курсе S3 (96 руб.) инвестор получит убыток 4 руб.
В случае формирования синтетической позиции (все варианты решения d2) доход зависит от стратегии инвестора. При паритете цен опционов синтетическая позиция полностью эквивалентна позиции по обычной акции, поэтому и ожидаемые результаты должны совпадать. Из формулы паритета опционов (см. выше) мы видим, что для формирования синтетической позиции инвестору нужно купить опцион колл и продать пут, что требует в сумме:
3 руб. – 0,56 руб. = 2,44 руб.
Инвестор тратит эту сумму из имеющихся у него 100 руб., а остаток в сумме:
100 руб. – 2,44 руб. = 97,56 руб.
размещает на трехмесячный депозит под 10%, и по окончании срока договора получает:
97,56 руб. · (1 + 0,1 · 3/12) = 100 руб.
Если через три месяца курс акции достигнет 104 руб. (S1), то инвестор исполнит опцион колл и выиграет 4 руб.
Если курс акции составит 100 руб. (S2), то опционы исполняться не будут, но инвестор останется «при своих».
Если курс акции составит только 96 руб. (S3), то опцион пут будет исполнен контрагентом, т.е. инвестор купит ее за 100 руб., и получит убыток 4 руб. Эти результаты заносим в ячейки Таблицы 3 для варианта решения d2 в случае состояния паритета опционов.
Наличие арбитражных возможностей дает инвестору следующие варианты действий. Если состояние паритета опционов нарушено, и курс акции в этот момент равен 101 руб. (High), то инвестор может занять ее у брокера и продать, купить опцион колл и продать пут, что даст ему следующий результат:
101 руб. – 3 руб. + 0,56 = 98,56 руб.
Эту сумму инвестор может разместить на трехмесячный депозит под 10% и получить:
98,56 руб. · (1 + 0,1 · 3/12) = 101,024 руб.
Если через три месяца курс акции достигнет 104 руб. (S1), то инвестор исполнит опцион колл, т.е. купит акцию за 100 руб., вернет ее брокеру, и получит:
101,024 руб. – 100 руб. = 1,024 руб.
Если курс акции достигнет 100 руб. (S2), то опционы исполняться не будут, инвестор купит акцию на спотовом рынке, вернет ее брокеру, его доход также составит 1,024 руб.
Если курс акции достигнет только 96 руб. (S3), то опцион пут будет исполнен контрагентом, инвестор купит у него акцию за 100 руб., вернет ее брокеру, его доход также составит 1,024 руб.
При наличии арбитражной возможности в другом направлении инвестор может поступить иначе. Например, если акция в этот момент стоит 99 руб. (Low), то инвестор может занять нужную сумму на три месяца под 10%, купить акцию, опцион пут, и продать колл, для чего потребуется сумма:
0,56 руб. + 99 руб. – 3 руб. = 96,56 руб.
Через три месяца долг составит:
96,56 руб. · (1 + 0,1 · 3/12) = 98,97 руб.
Если к этому моменту курс акции достигнет 104 руб. (S1), то опцион колл исполнит контрагент, т.е. инвестор продаст ему акцию за 100 руб., рассчитается за кредит, и получит:
100 руб. – 98,97 руб. = 1,03 руб.
Если курс акции будет равен 100 руб. (S2), то инвестор продаст акцию на спотовом рынке, рассчитается за кредит, и получит также 1,03 руб.
Наконец, если курс акции достигнет только 96 руб. (S3), то инвестор сам исполнит опцион пут, т.е. продаст акцию за 100 руб., рассчитается за кредит и также получит 1,03 руб. Результаты реализации арбитражных возможностей заносим в соответствующие ячейки Таблицы 3 для решения d2.
Таблица 3. Состояния узла полезности.
№ | Решение D | Цена акции через 3 месяца | Полезность U, руб. | ||
Parity | Low | High | |||
1 | d1 | S1 | 4 | 4 | 4 |
2 | d1 | S2 | 0 | 0 | 0 |
3 | d1 | S3 | -4 | -4 | -4 |
4 | d2 | S1 | 4 | 1,03 | 1,024 |
5 | d2 | S2 | 0 | 1,03 | 1,024 |
6 | d2 | S3 | -4 | 1,03 | 1,024 |
После завершения этой работы инициализируем модель, и можем приступать к вероятностным выводам (Рис. 3). По результатам расчета полезности довольно трудно судить заранее о том, какое решение даст лучший результат. Например, можно видеть, что в случае выбора обычной акции отрицательных результатов (убытков) больше, но при этом суммы дох��дов выше, чем при выборе синтетической позиции.
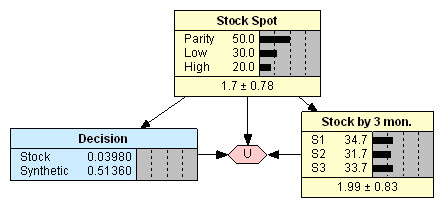
После инициализации модель подтверждает положительный результат инвестирования в случае выбора синтетической позиции в отсутствие других свидетельств о состоянии рынка. Таким образом, решением инвестора в условиях полной неопределенности должно быть формирование синтетической позиции. Однако если бы инвестор мог знать заранее, что курс акции достигнет 104 руб., то он мог бы получить больший доход (Рис. 4). При отсутствии информации об арбитражных возможностях этот вариант является самым выгодным.
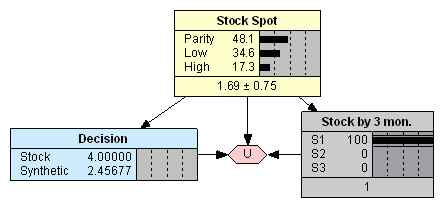
Следующее состояние, тем не менее, показывает, что если бы было известно, что курс акции через три месяца не превысит цену исполнения, то преимущество вновь было бы на стороне синтетической позиции (Рис. 5).
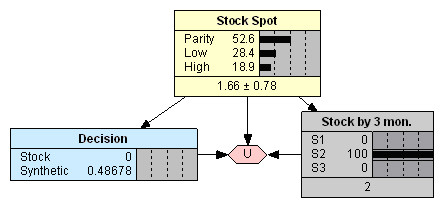
Наличие (отсутствие) арбитражных возможностей усложняет вывод. Например, при отсутствии априорной информации о курсе акции состояние, соответствующее паритету опционов, использованных для формирования синтетической позиции, делает выбор безразличным (Рис. 6), так как оба решения дают одинаковый убыток.
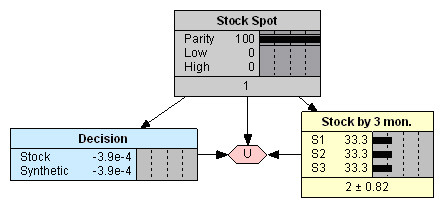
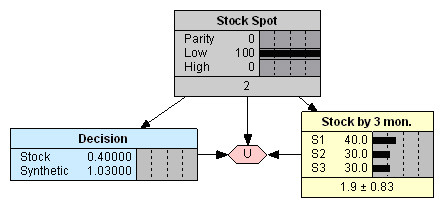
Появление арбитражных возможностей, как при пониженной цене спот акции относительно состояния паритета опционов, так и при повышенной, вновь дает преимущество в выигрыше в случае выбора синтетической позиции (Рис. 7 и 8). При этом убыток в случае выбора обычной акции мог бы быть максимальным.
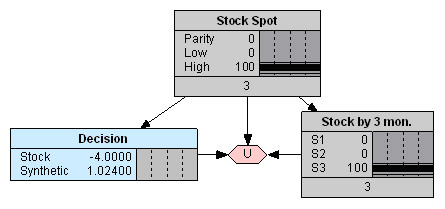
Конечно, следует отметить, что построенная диаграмма влияния является лишь исходным «каркасом» модели. В более сложную модель, приближенную к реальности, необходимо вводить дополнительные переменные, с помощью которых будет учитываться влияние:
финансового состояния компании-эмитента акции;
состояния отрасли, к которой принадлежит данная компания;
макроэкономических показателей состояния отрасли и экономики в целом;
уровня и тенденции изменения процентных ставок;
текущего состояния рынка производных финансовых инструментов (опционов), фондового рынка в целом, и других показателей.
Остается добавить, что русскоязычной (в т.ч. переводной) литературы практического плана по синтетическим инструментам почти нет, поэтому информацию приходится собирать по крупицам. Приведу лишь два источника, в которых есть полноценные главы, посвященные этой теме.
Литература:
1. Буренин А.Н. Форварды, фьючерсы, опционы, экзотические и погодные производные. М.: НТО, 2011.
2. Маршалл Джон Ф., Бансал Викул К. Финансовая инженерия: Полное руководство по финансовым нововведениям / пер. с англ. М.: ИНФРА-М, 1998.