Tereshkov Aug 2 2021 at 12:47

Заставляем компьютер выводить общие законы физики из наблюдений

5 min

Programming*Compilers*Machine learning*PhysicsAstronomy

Как правило, компьютеры в естественных науках занимаются либо получением чисел из чисел, либо выводом формул из формул. Попытаемся решить более экстравагантную задачу — из набора численных данных вывести формулы общих физических законов, причём не только неизвестные параметры формул, но и сам их вид. В качестве примера рассмотрим задачу о кеплеровых орбитах — в частности, о движении спутника вокруг Земли, и получим законы сохранения энергии и момента импульса, из которых в небесной механике и выводятся эллипсы орбит и законы Кеплера.

Вдохновением для этих занятий послужила замечательная статья из Science, которая убедила меня и многих других в том, что к таким задачам в принципе можно подступиться. Как и у авторов статьи, наш пример будет немного игрушечным, хоть и для совсем другой физической системы. Более того, мы ещё сильнее ограничим пространство поиска (до $2^{64}$ формул, что тоже немало), зато обойдёмся без 32 процессорных ядер и без GPU, а решение получим меньше чем за минуту против десятков минут или даже пары дней, как в статье. Для всего этого нам понадобится лишь 300 строк кода на C — и никаких фреймворков.

Вход и выход

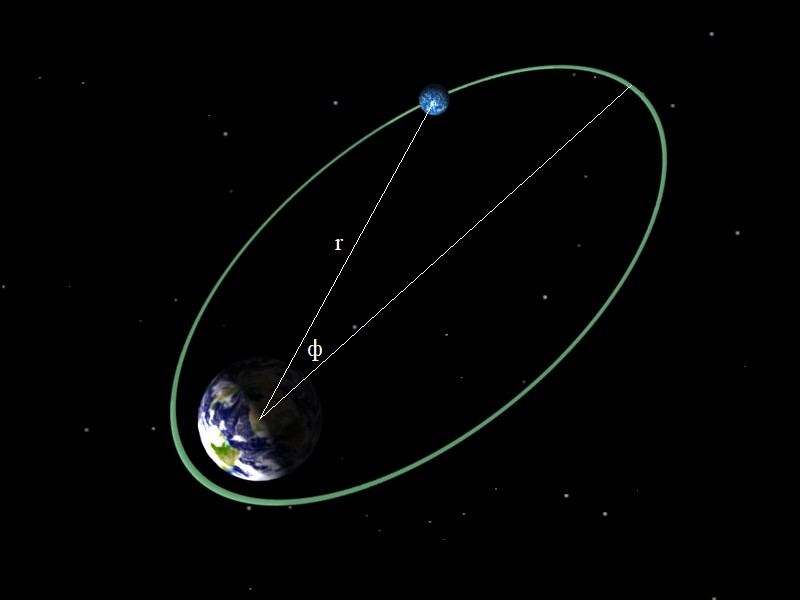
Итак, будем рассматривать движение спутника вокруг Земли, подчиняющееся закону всемирного тяготения $F={GMm}/{r^2}$ , где для удобства возьмём GM=1 и m=1 . Источником измерительных данных будет служить симулятор, выдающий массив полярных координат спутника в плоскости орбиты: расстояний и углов $\phi$ . Для основного алгоритма поиска симулятор является чёрным ящиком, так что никакого закона тяготения алгоритм поиска изначально не знает.

Вопрос о выходных данных сложнее. В ответе требуется иметь не число и не массив чисел, а формулу. Представим её в виде байт-кода простейшей стековой виртуальной машины, которая может оперировать следующими базовыми понятиями:

Действительные переменные
Целые числовые константы от 0 до 5
Сложение, вычитание, умножение, деление
Возведение в квадрат

Система команд виртуальной машины

Код	Мнемоника	Значение
0	0	Загрузка константы 0
...	...	...
5	5	Загрузка константы 5
6	a	Загрузка переменной a
...	...	...
9	d	Загрузка переменной d
10	+	Сложение
11	-	Вычитание
12	*	Умножение
13	/	Деление
14	^	Возведение в квадрат
15	.	Нет операции

Такой ограниченный набор позволяет уместить каждую команду виртуальной машины в 4 бита. Если теперь дополнительно ограничить длину формулы 16 командами, то любая формула будет представима в виде одного 64-битного целого числа. Это сулит исключительные удобства: тип данных uint64_t поддерживается как родной современными процессорами и компиляторами, любая формула целиком помещается в регистр процессора и легко передаётся в функции по значению. По сравнению с подходом авторов статьи в Science, всё это сильно упрощает и ускоряет обработку данных, а в конце концов позволяет быстро получить решение даже на весьма убогой машине.

В качестве четырёх допустимых переменных a, b,c, d у нас будут выступать расстояния и углы $\phi$ , взятые от симулятора, а также скорости их изменения (иными словами, производные по времени) $\dot r$ и $\dot \phi$ . Коль скоро мы взялись искать законы сохранения, то решением для нас будет любая формула, которая при подстановке в неё переменных, соответствующих истинному движению спутника, не будет изменять своего значения вдоль всей его орбиты, как бы ни менялись при этом сами переменные:

$f(r, \phi, \dot r, \dot \phi)=const$

Критерии качества формулы

Условие f=const можно записать и иначе: скорость изменения самой сохраняющейся величины должна быть нулевой, то есть $\dot f=0$ . Разумеется, из-за численных ошибок (а в реальной жизни ещё и из-за ошибок измерения) ни одна найденная нами формула не будет удовлетворять этому условию точно. Следовательно, мы можем лишь пожелать иметь как можно меньшее среднеквадратичное значение $RMS(\dot f)$ , посчитанное вдоль всей орбиты. Тогда для удобства ранжирования формул по качеству можно взять величину $S=-lg(RMS(\dot f))$ . Чем она больше, тем точнее сохраняется найденная величина .

Однако сразу же приходит понимание того, что существует множество формул вроде f = 0 или f=r/r+42 , которые совершенно постоянны и будто бы идеально соответствуют выбранному критерию качества (для них $S=\infty$ ), однако на самом деле тривиальны, поскольку просто не зависят ни от одной переменной. Поэтому необходим дополнительный критерий: у функции должны быть ненулевые составляющие градиента, то есть ненулевая чувствительность к её аргументам. В зависимости от того, к каким именно аргументам (среди четырёх имеющихся) мы потребуем чувствительности, алгоритм будет сходиться к разным сохраняющимся величинам.

Закон сохранения момента импульса

Начнём с очевидного. Потребуем ненулевой чувствительности к и запустим поиск максимума случайным перебором формул (ничего проще и тупее и не придумаешь!). Уже через несколько секунд начнут попадаться формулы вроде da^..*5/........ .

Попробуем расшифровать эту формулу. Воспользуемся мнемониками команд нашей виртуальной машины. Учтём соответствия переменных $a=r, d=\dot \phi$ . Наконец, вспомним о том, что последовательность команд стековой машины фактически содержит формулу вычисляемого выражения в обратной польской записи. Тогда окажется, что компьютер предлагает нам формулу $f=\dot \phi r^2 /5$ . Делитель 5 не играет никакой роли в том, будет ли величина сохраняться или нет, и его можно смело отбросить. Получается, что мы нашли соотношение

$r^2 \dot \phi=const$

Это не что иное, как закон сохранения момента импульса. Момент импульса — это, грубо говоря, произведение импульса тела на плечо . У нас m=1 , $v=r \dot \phi$ , так что закон имеет в точности тот вид, который мы и обнаружили. Можно даже вычислить конкретное значение этой константы. Для той орбиты, которая заложена в симулятор, получается $r^2 \dot \phi=2$ . Итак, у нас есть первый нетривиальный результат. Его наглядной геометрической трактовкой служит второй закон Кеплера:

За равные промежутки времени радиус-вектор спутника заметает равные площади.

Закон сохранения энергии

Закон сохранения энергии найти намного сложнее. Начинать следует с того, чтобы направить поиск в нужное русло, а именно потребовать, чтобы сохраняющаяся величина имела ненулевую чувствительность к скоростям $\dot r$ и $\dot \phi$ . В противном случае алгоритм будет постоянно натыкаться на формулы момента импульса. Их много, они рассеяны по всему пространству поиска, выглядят совершенно по-разному, украшены всевозможными бесполезными множителями и делителями, но физически все выражают один и тот же закон сохранения момента импульса, с которым мы уже разобрались. Теперь эти формулы стали для нас помехой, и найти среди них гораздо более сложные и редкие формулы закона сохранения энергии очень трудно. Когда эта помеха наконец исключена, обнаруживается, что случайный поиск не приносит больше ничего. Разумеется, бессмысленно надеяться и на исчерпывающий перебор среди всех $2^{64}$ формул. Ну а поскольку мы ищем дискретную величину, не даст результата и градиентный спуск.

Однако ничто не мешает применить, например, генетические алгоритмы или имитацию отжига. Наш метод будет похож на имитацию отжига. Создадим начальный набор случайных формул. На каждом шаге "отжига" будем вносить в формулы небольшие случайные модификации (менять одну из 16 команд виртуальной машины). Если критерий качества формулы при этом возрос, то есть S'>S , то модифицированная формула заменяет исходную. Если же он снизился, то модифицированная формула тоже может заменить исходную, но лишь с вероятностью p=exp((S'-S)/T) , где — "температура". Обычно по мере "отжига" уменьшают "температуру", однако даже без этого "охлаждения" удаётся получить результат. Спустя 1000 шагов при размере набора 500 формул часто находится несколько подходящих вариантов (их точное количество и вид зависят от генератора случайных чисел). Например:

.c^d3a-*d5.5++-+
d5.d+da.*-c.^++.

Расшифруем первую формулу (вторая даёт то же самое):

$f=\dot r^2 + \dot \phi (3-r)-(\dot \phi+5+5)=\dot r^2 - \dot \phi(r-2)-10$

После отбрасывания бесполезного члена -10 остаётся странное выражение, как будто бы не похожее ни на один из известных законов сохранения:

$\dot r^2 - \dot \phi(r-2)=const$

Однако можно вспомнить, что раньше мы получили закон сохранения момента импульса в виде $r^2 \dot \phi=2$ . Если теперь подставить этот момент импульса вместо 2, то получим:

$(\dot r^2 + r^2 \dot \phi^2)/2-1/r=const$

А это уже закон сохранения энергии. Первый член представляет собой кинетическую энергию, в которой квадрат скорости выражен в полярных координатах. Второй член -1/r описывает потенциальную энергию гравитационного притяжения, раз уж мы приняли GM=1 . Их сумма, то есть полная энергия, постоянна.

Итак, мы нашли в аналитическом виде два фундаментальных закона сохранения, опираясь лишь на численные данные о координатах движущегося спутника, с чем себя и поздравим.

Код на GitHub

Tags:

Hubs: