Приветствую читателей Хабра!
С момента моего дебюта на этой платформе многое изменилось, в том числе и моя карьера. Благодаря статье меня заметила компания и теперь, будучи инженером-исследователем в компании "Geogracom", я столкнулся с непростой задачей, которая заставила изучить новые для себя техники и архитектуры.
В этой статье мы рассмотрим подход к решению задачи классификации облака точек, основанный на использовании воксельного представления и сиамских нейронных сетей с 3D свертками. Задача стала особенно актуальной, когда столкнулся с необходимостью классифицировать данные, имея всего 10 примеров для каждого класса, что существенно ограничивало применение традиционных методов машинного обучения.
Надеюсь многим будет интересно и полезно!
История задачи
В нашем проекте мы столкнулись с задачей, которая на первый взгляд казалась довольно простой: необходимо было классифицировать объекты по части большого файла формата LAS, распределяя их по трем классам - провода, деревья и мосты, имея всего по 10 примеров для каждого класса. Сразу отмечу, что с классификацией проводов сложностей не возникло благодаря их характерным особенностям (очень маленькое количество точек на один объект), однако деревья и мосты "кинули вызов" из-за их морфологического разнообразия �� часто визуального сходства.
Использование классических подходов, основанных на статистических характеристиках — среднем значении, дисперсии, плотности распределения точек и тд — не принесло ожидаемых результатов. Разнообразие форм деревьев и схожесть некоторых мостов с ними существенно усложнило задачу, до такой степени, что даже я периодически не мог классифицировать объекты на основе представленных данных.
Первоначально я не рассматривал возможность использования нейронных сетей из-за очень ограниченного объема данных. Столкнувшись с неэффективностью традиционных методов и ограниченными сроками, я задался вопросом о возможности обучения нейронной сети на таком малом количестве примеров, вспомнив, что по нескольким фотографиям человека учат сеть его идентифицировать.
В ходе "гуглинга" я обнаружил, что сиамские архитектуры уже успешно применяются для решения подобных задач, благодаря их способности эффективно работать с малым объемом данных. Вспомнил о 3D свертке и было принято решение опробовать данный метод.
Но оставался еще один вопрос - разное количество точек в разных объектах для классификации. Эту проблему удалось решить с помощью перехода к воксельному представлению, напоминая знакомые концепции обработки изображений в работе с трехмерными данными и значительно упростив процесс классификации.
А теперь расскажу подробнее об этом и покажу реализацию в коде.
Что такое воксели?
Воксели, или объемные пиксели, представляют собой трехмерные аналоги двухмерных пикселей, которые используются в графике и обработке изображений. Это маленькие кубики, которые в совокупности формируют трехмерное пространство, позволяя представить объемные данные в дискретизированной форме.
Воксельное представление позволяет эффективно анализировать сложные трехмерные структуры, делая его идеальным для работы с облаками точек, где требуется дискретизация непрерывного трехмерного пространства. Этот подход значительно упрощает обработку и анализ трехмерных данных, обеспечивая единообразную и упорядоченную структуру для последующего анализа и визуализации.


Вроде не сложно для понимания. Думаю, что все мы хотя бы раз встречались с таким представлением данных (Любителям minecraft привет).
С вокселями разобрались. Теперь давайте посмотрим в коде переход от point cloud в воксели и сохраним результат в формате ply для наглядности.
Нам понадобятся понадобятся библиотеки: laspy, open3d, torch, numpy. Минимальный джентльменский набор при работе с point cloud)))
Код
Функции
def read_las_file(file_path):
"""
Читает файл LAS и возвращает координаты точек.
"""
with laspy.open(file_path) as file:
las = file.read()
points = np.vstack((las.x, las.y, las.z)).transpose()
return pointsdef normalize_points(points):
"""
Нормализует координаты точек, помещая их в единичный куб.
"""
min_point = np.min(points, axis=0)
max_point = np.max(points, axis=0)
normalized_points = (points - min_point) / (max_point - min_point)
return normalized_pointsdef voxelize(points, grid_size):
"""
Преобразует точки в воксели с учетом размера сетки.
"""
normalized_points = normalize_points(points)
indices = np.floor(normalized_points * grid_size).astype(int)
indices = np.clip(indices, 0, grid_size - 1)
unique_voxels = np.unique(indices, axis=0)
return unique_voxelsdef create_voxel_cubes(voxels, voxel_size=1):
"""
Создает маленькие кубы для визуализации каждого вокселя.
"""
cubes = []
for voxel in voxels:
center = voxel * voxel_size
cube = o3d.geometry.TriangleMesh.create_box(width=voxel_size,
height=voxel_size,
depth=voxel_size)
cube.translate(center - np.array([voxel_size/2, voxel_size/2, voxel_size/2]))
cubes.append(cube)
return cubesdef save_as_ply(cubes, file_name):
"""
Сохраняет воксельные кубы в файл PLY.
"""
mesh = o3d.geometry.TriangleMesh()
for cube in cubes:
mesh += cube
o3d.io.write_triangle_mesh(file_name, mesh)Основная часть
input_file_path = 'input_path'
output_file_path = 'output_path'
grid_size = 100
files = [f for f in os.listdir(input_file_path) if f.endswith('.las')]
for i in files:
points = read_las_file(os.path.join(input_file_path, i))
voxels = voxelize(points, grid_size=grid_size)
cubes = create_voxel_cubes(voxels)
base = os.path.splitext(i)[0]+'.ply'
output_path = os.path.join(output_file_path, base)
save_as_ply(cubes, output_path)Результат
В итоге мы перешли от point cloud в воксели


Сиамские нейронные сети
Общее описание и архитектура
Сиамская нейронная сеть – это тип архитектуры, включающей две или более идентичных подсети с одинаковыми параметрами, обновляемыми зеркально. Эта конфигурация предназначена для оценки сходства входных данных на основе их признаков. В отличие от традиционных нейронных сетей, которые требуют обновления при добавлении новых классов и большого объема данных для обучения, сиамские сети изучают функцию сходства, позволяя классифицировать новые классы данных без повторного обучения сети. Это делает их особенно полезными в задачах, где требуется гибкость и эффективность при ограниченном наборе данных.
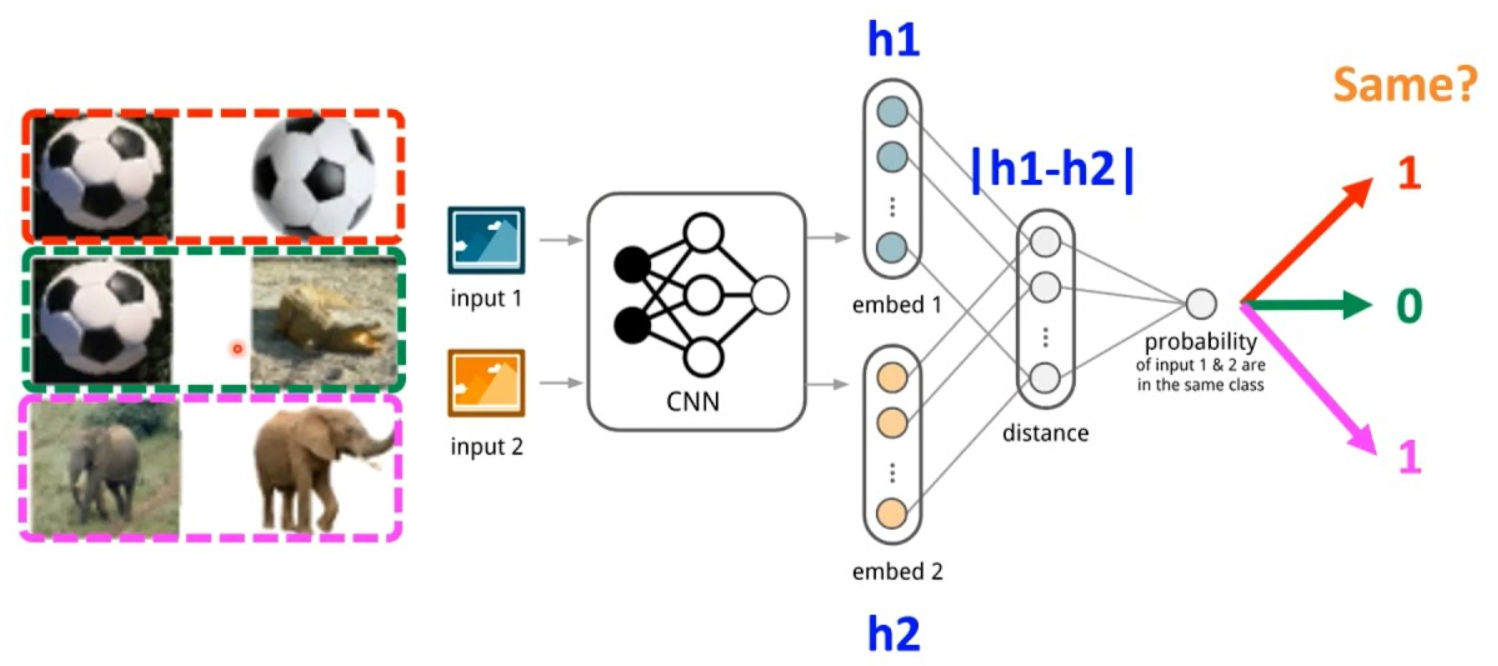
Функция потерь Triplet Loss
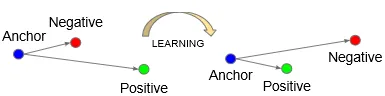
Давайте начнем с аналогии. По крайней мере мне было проще понять именно так. Отмечу, что на схеме выше была представлена сеть с двумя подсетями, но далее буду писать про сеть с тремя подсетями.
Представьте, что вы участвуете в соревновании по бегу с двумя друзьями, где один друг всегда должен финишировать раньше другого. Ваша задача — максимизировать расстояние между вторым и третьим бегунами, сохраняя при этом первого ближе к себе. В контексте сиамских сетей, Triplet Lossработает аналогично, где "бегуны" — это элементы данных: "anchor" (аналог вас), "позитивный" пример (ваш друг, который должен быть ближе) и "негативный" пример (друг, от которого нужно оторваться).
Формула функции потерь Triplet Loss в контексте нейронных сетей выражается следующим образом:
где:
L(a, p, n) обозначает потерю для тройки: anchor (a), позитивный (p) и негативный пример (n)
d(a, p) и d(a, n) представляют собой расстояния (обычно Евклидовы) между anchor и позитивным примером и между анкером и негативным примером соответственно.
margin (порог) — это гиперпараметр, задающий минимальное расстояние, которое должно быть между позитивными и негативными парами.
Элементы, влияющие на обучение и настраиваемые параметры:
Расстояние d: выбор функции расстояния влияет на способ измерения различий между примерами.
Margin: пороговое значение, которое определяет, насколько далеко негативные примеры должны быть от анкера по сравнению с позитивными примерами. Больший margin способствует увеличению различий между классами в пространстве признаков.
Тут так же видно, что нет сложных формул, поэтому понять достаточно просто. Меня это очень удивило, что столь простая идея (в плане архитектуры и функции потерь) работает настолько хорошо. Не большой спойлер - модель после обучения не ошибается на валидации, на тесте и в процессе эксплуатации, по крайней мере "пока что".
Реализация нейронной сети
Теперь давайте посмотрим на реализацию нейронной сети и на цикл обучения. Замечу, что сама по себе сеть примитивная, но вся красота заключается именно в цикле обучения и в функции потерь.
Функции
def train_epoch(model, dataloader, loss_fn, optimizer, device):
model.train()
running_loss = 0.0
for data in dataloader:
anchor, positive, negative = [d.to(device) for d in data]
optimizer.zero_grad()
anchor_output = model(anchor)
positive_output = model(positive)
negative_output = model(negative)
loss = loss_fn(anchor_output, positive_output, negative_output)
loss.backward()
optimizer.step()
running_loss += loss.item()
return running_loss / len(dataloader)def validate_epoch(model, dataloader, loss_fn, device):
model.eval()
running_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for data in dataloader:
anchor, positive, negative = [d.to(device) for d in data]
anchor_output = model(anchor)
positive_output = model(positive)
negative_output = model(negative)
loss = loss_fn(anchor_output, positive_output, negative_output)
running_loss += loss.item()
total += anchor.size(0)
correct += (torch.norm(anchor_output - positive_output, dim=1) <
torch.norm(anchor_output - negative_output, dim=1)).sum().item()
accuracy = 100 * correct / total
return running_loss / len(dataloader), accuracydef log_to_file(log_path, epoch, train_loss, val_loss, val_accuracy):
with open(log_path, "a") as log_file:
log_file.write(f"Epoch {epoch}, Train Loss: {train_loss}, Validation Loss: {val_loss}, Validation Accuracy: {val_accuracy}%\n")
def save_model(model, epoch, save_path="model_checkpoint"):
if not os.path.exists(save_path):
os.makedirs(save_path)
torch.save(model.state_dict(), os.path.join(save_path, f"model_epoch_{epoch}.pth"))
Архитектура
class Siamese3DNetwork(nn.Module):
def __init__(self, grid_size):
super(Siamese3DNetwork, self).__init__()
self.conv_layers = nn.Sequential(
nn.Conv3d(1, 32, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.MaxPool3d(kernel_size=2, stride=2),
nn.Conv3d(32, 64, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.MaxPool3d(kernel_size=2, stride=2),
nn.Conv3d(64, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(),
nn.MaxPool3d(kernel_size=2, stride=2)
)
self.flattened_size = 128 * (grid_size // 8) ** 3
self.fc_layers = nn.Sequential(
nn.Linear(self.flattened_size, 512),
nn.ReLU(),
nn.Linear(512, 256)
)
def forward(self, x):
x = self.conv_layers(x)
x = x.view(-1, self.flattened_size)
x = self.fc_layers(x)
return xЦикл обучения
input_file_path = 'input_path'
grid_size = 100
log_path = 'log_path.txt'
batch_size = 8
num_epochs = 30
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
dataset = VoxelTripletDataset(root_dir=input_file_path, grid_size=grid_size)
train_size = int(0.8 * len(dataset))
val_size = len(dataset) - train_size
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
model = Siamese3DNetwork(grid_size)
triplet_loss = nn.TripletMarginLoss(margin=9.0, p=2)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
model.to(device)
for epoch in range(num_epochs):
train_loss = train_epoch(model, train_loader, triplet_loss, optimizer, device)
val_loss, val_accuracy = validate_epoch(model, val_loader, triplet_loss, device)
print(f"Epoch {epoch+1}, Train Loss: {train_loss}, Validation Loss: {val_loss}, Validation Accuracy: {val_accuracy}%")
log_to_file(log_path, epoch+1, train_loss, val_loss, val_accuracy)
save_model(model, epoch+1)Результаты
Проведенные эксперименты и тестирование выбранной архитектуры наглядно мне показали эффективность и скорость. Модель демонстрирует великолепные результаты, точно классифицируя как валидационный, так и тестовый наборы данных без ошибок. Отд��льно стоит отметить высокую скорость предсказаний даже при работе на процессоре, что является важным критерием для компании
Выводы
Весь процесс от исследования до реализации занял несколько дней, но результаты оказались действительно впечатляющими как в плане точности, так и скорости. В ходе работы я рассмотрел несколько альтернативных подходов для работы с небольшим объемом данных. Хотя некоторые из них показались сложными для быстрого изучения и написания, они остаются в запасе для реализации. Уверен, что встречусь еще ни раз с задачами, где простые решения не принесут желаемого результата, и тогда придется обратиться к более сложным методам. Буду рад, если кого-то натолкнул на мысли в их собственных проектах. Надеюсь, что вам было интересно и полезно. Уверен, что это не последняя моя статья на Хабре :-) Самое лучшее для закрепления материала- это попытаться объяснить кому-то.