
Специальная теория относительности - удивительная теория, которая опровергла многие представления о мире, в которых человечество не сомневалось всю историю своего существования.
Многие слышали про волшебства вроде замедления времени, сокращения длины, относительности одновременности, парадокса близнецов и т.д., но мало кто понимает почему так происходит. В этой статье я хочу наглядно показать, что все это проще, чем кажется на первый взгляд.
Для иллюстраций я написал интерактивный визуализатор СТО, работающий в браузере. Ссылка на него и исходники проекта в конце статьи.
Я потратил много времени на чтение статей и просмотр видеороликов, но все это не давало мне понимания, а лишь запутывало и вызывало новые вопросы. Многие материалы противоречат друг другу, некоторые вообще транслируют откровенную дезинформацию. Да, можно придерживаться принципа “Shut up and calculate” и просто пользоваться формулами преобразования координат из учебников, но мне хотелось получить более интуитивное понимание процессов. Все же теория относительности - не квантовая механика, ее должно быть возможно понять.
После долгого изучения, я смог отфильтровать и объединить разрозненную информацию в единую картину. Оказалось, все не так сложно, и сейчас я хочу поделиться результатом. Все цитаты ученых и исторические события немного искажены для упрощения повествования.
Вступление
Начнем с пространственно-временной диаграммы. По горизонтальной оси будет положение в пространстве в метрах, а по вертикальной - время в секундах.
В середине некоторое начало координат, где нахожусь я как наблюдатель.

Возьмем двух котов, за которыми мы начнем наблюдение в нулевой момент времени. Один из них спит. Он неподвижен относительно нас, поэтому его мировая линия - просто вертикальная прямая.
Другой кот начинает бежать вправо с некоторой скоростью. Угол наклона синей линии определяется скоростью кота. Видно, что угол наклона 45 градусов, значит он бежит ровно 1м/с.
Спойлер
Скорость равна тангенсу угла наклона синей линии (относительно вертикальной оси) т.к. тангенс по определению равен отношению противолежащего катета к прилежащему.
Каждую секунду мы как-бы фотографируем положения котов, что соответствует их изображениям на мировых линиях.
Все знают, что движение относительно. Бегущий кот движется относительно нас так же как и мы относительно него. Нет какого-то абсолютного движения, которое лучше других. Это называется принципом относительности Галилея и ему уже 400 лет.
Попробуем догнать бегущего кота и посмотреть как будет выглядеть эта диаграмма в его системе отсчета (в ней бегущий кот неподвижен, а спящий - движется в противоположную сторону). Для этого нам нужно просто сдвинуть все точки диаграммы влево вдоль горизонтальных линий так, чтобы линия бегущего кота стала вертикальной (неподвижной). Расстояния между котами в каждый момент времени при этом должны оставаться неизменными.
Пока что все хорошо, никакой чертовщины не происходит. Такое преобразование называется преобразованием Галилея. Оно понятное, логичное и мы без задней мысли пользовались им многие сотни лет.
Проблемы
А потом в конце 19го века появилась внезапная новость: Эксперименты показали, что скорость света одинакова во всех системах отсчета. Как бы ни двигался источник света относительно наблюдателя или наблюдатель относительно источника, в какую сторону и в каком направлении - измеренная скорость света всегда одинакова и равна 299 792 458 м/с.

То есть скорость котов, скорость звука, скорость чего угодно в разных системах отсчета разная, а скорость света - нет. Преобразования Галилея на свет просто не действуют.

Такую информацию сложно принять, ведь она противоречит базовой интуиции и всей физике, известной на тот момент. Многие ученые пытались найти ошибку, но все было тщетно.
Ничего не оставалось, кроме как плюнуть на все это и изобрести физику заново.

Такую физику, чтобы скорость света была постоянна, и при этом другие физические законы не сломались.
Как это сделать? Что ж, откроем пространственно-временную диаграмму и попытаемся что-то придумать.
Для начала нарисуем кота, который бежит со скоростью света. Но эта скорость настолько большая, что линия кота будет практически горизонтальна (ведь скорость определяется углом наклона линии). Поэтому скукожим диаграмму по горизонтали в 300 миллионов раз. Таким образом, линии горизонтальной сетки будут отмерять уже не метры, а световые секунды.
В таком масштабе линия бегущего со скоростью света кота будет расположена под углом 45 градусов (1 световая секунда в секунду). И для наглядности я нарисовал еще одного кота, который тоже бежит со скоростью света, но в противоположную сторону.
Если мы начнем двигаться относительно неподвижного спящего кота то линии световых котов будут менять свой угол наклона, что нам не подходит, ведь это противоречит эксперименту.
Значит, теперь наша задача - сделать невозможное. Изменить преобразования Галилея так, чтобы выполнялось три условия:
То, ради чего мы все это затеяли: линии световых котов не должны менять своего угла. Это будет значить, что скорость света будет для нас всегда одинакова, независимо от того, с какой скоростью мы движемся относительно источника этого света.
Новое преобразование должно быть совместимо со старым. Т.е. на обычных скоростях все должно работать как работало до этого.
И еще желательно, чтобы прямые линии оставались прямыми (например, мировая линия бегущего с постоянной скоростью кота должна оставаться прямой), иначе будет нарушен закон сохранения энергии.
И тут приходит Эйнштейн с друзьями и заявляет:
Мы кое-что придумали. Но придется пожертвовать евклидовостью нашего пространства-времени.

Чтобы понять что они такое придумали, нужно сказать пару слов о евклидовом пространстве.
Евклидово пространство
В любом пространстве можно поставить две точки. Будь это привычное “пространственное” пространство с осями X-Y-Z, или пространство-время, как у нас на диаграмме с осями X-t, или любое другое. И между этими двумя точками можно измерить расстояние.
Для измерения расстояния мы привыкли использовать теорему Пифагора. На двумерной плоскости оно выглядит так:

Квадрат длины зеленого отрезка равен сумме квадратов длин его проекций на оси.
Формула, которая измеряет расстояние между двумя точками по их координатам называется метрикой. Пространства с такой метрикой называются евклидовыми. В других (неевклидовых) пространствах метрики другие.
Важно, что расстояния между точками не меняются при движениях и вращениях системы координат. Как бы мы ни двигали и не вращали нашу пару осей относительно пары точек, вычисленное по этой формуле расстояние между ними не изменится.

На нашей евклидовой пространственно-временной диаграмме расстояние между точками будет таким:
Спойлер
Обычно переменную t для удобства домножают на скорость света, чтобы временнАя координата тоже измерялась в метрах.
Пространство Минковского
Так что же конкретно предложили Эйнштейн с друзьями? Они сказали:
А давайте в метрике плюс заменим на минус, и вместо сдвигов будем вращать точки вокруг центра координат.
Посмотрим. Меняем в метрике плюс на минус, получаем следующее:
Новая метрика означает новое пространство. Пространство с такой метрикой назвали пространством Минковского.
Теперь нужно вращать. Но что вообще это значит?
Вращение - это такая операция, при котором расстояние от точки до центра вращения остается неизменным. Но тут нам предлагают вращать в таком пространстве, где это самое расстояние до центра считается по формуле с минусом вместо плюса:
(Мы вращаем вокруг центра координат, поэтому ∆x = x, а ∆t = t.)
Если в нормальном вращении точки движутся по окружностям, то по каким траекториям они будут двигаться теперь?
Эти новые траектории должны представлять собой линии равных расстояний от центра. Для наглядности нарисуем пунктиром такие траектории, для которых расстояния до центра равно целым числам, так же, как до этого мы рисовали горизонтальные прямые, отмечающие секунды.
Засунем эту формулу в программу и посмотрим как это отразится на котах:

Странно. Вроде, все выглядит так же, как было изначально. Что-то тут не так. Попробуем снова скукожить диаграмму по горизонтали так, чтобы сетка отмеряла световые секунды и мы увидели световых котов.
Оказалось, что горизонтальные пунктирные прямые, по которым раньше смещались коты при изменении скорости наблюдателя, стали кривыми. Но мы это заметили только отдалив масштаб так, чтобы в график попадали очень высокие скорости. Кстати, эти новые кривые линии называются гиперболами.
А теперь попробуем повращать. Если в нормальном евклидовом пространстве для вращения точки вокруг центра координат, нужно умножить ее координаты на всякие синусы и косинусы угла поворота, то в пространстве Минковского это немного проще:

Это называется преобразованиями Лоренца. Вместо угла тут скорость относительно наблюдателя. Кстати, по этим формулам видно, что если подставить нулевую скорость относительно наблюдателя или бесконечную скорость света, то знаменатели превращаются в единицу и формулы превращаются в обычные преобразования Галилея.
Посмотрим как теперь будут смещаться коты при изменениях скорости наблюдателя.
Обратите внимание, что коты, которые находятся на линиях, соответствующих скорости света, остаются на этих линиях при любых скоростях наблюдателя.
Это значит, что как бы быстро ни двигался наблюдатель, световые коты все равно убегают от него со скоростью света.
Похоже, мы добились того, чего хотели:
При любых скоростях наблюдателя, коты на световых прямых остаются на них
В масштабе маленьких скоростей все работает так же, как работало раньше
Осталось проверить соответствие третьему требованию: чтобы прямые линии оставались прямыми. Для этого расположим пять спящих котов в разных координатах и посмотрим что будет, если мы начнем двигаться мимо них с огромной скоростью.
Обратите внимание на точки котов. Они сдвигаются вдоль гипербол, но линии, их соединяющие, всегда остаются прямыми.
Отлично, все работает. Мы изобрели такой мир, в котором постоянство скорости света не выглядит как чушь. Но это привело к катастрофическим последствиям, которые изменили всё.
Итак, подытожим: Раньше при увеличении скорости бегущего кота, его точки смещались вдоль горизонтальных линий, соответствующих одинаковому времени. А теперь эти линии стали кривыми.
Получается, теперь точки смещаются не только по горизонтали, но еще и по вертикали. А по вертикали то мы отмеряем время. Вот тут и начинается основное веселье.

Чтобы проиллюстрировать эффект замедления времени, выдадим нашим котам часы и еще раз посмотрим на диаграмму.

Мы неподвижны относительно спящего кота, поэтому для нас гиперболы и прямые линии находятся на одной высоте. Его часы тикают нормально. А бегущий кот пересекает гиперболы реже, чем горизонтальные прямые. Поэтому когда у нас часы натикали 6 секунд, у бегущего кота натикало меньше пяти. Получается, для нас время у бегущего кота идет замедленно, но сам он этого не замечает.
Разница во времени будет тем больше, чем выше его скорость (длина красного отрезка в треугольнике). Точно также симметрично происходит в системе бегущего кота. Если мы его догоним и посмотрим на спящего, увидим, что теперь у спящего время замедлено:

Итак, спящий кот думает. что время замедлено у бегущего, а бегущий - что у спящего.
Проиллюстрируем это на примере двух космических кораблей, на которых установлены одинаковые периодично мигающие лампочки. Как только один из них начинает двигаться, другой видит, что лампочка на первом стала мигать реже. И цвет ее стал красным, ведь замедление времени вызывает также и уменьшение частоты испускаемого света.
Но если мы будем двигаться вместе с ним, то увидим, что наоборот у неподвижного корабля ламбочка мигает реже и краснее.
Получается, время теперь относительно!
Некоторые говорят, что физики сами себе палки в колеса вставляют. Придумали какую-то хитрую модель пространства, а потом удивляются, что возникают странности. В реальности то это ни на что не повлияет.
Чтобы проверить реальность ли это или просто математический трюк, попросим бегущего кота пробежать немного (например, 4 секунды по его часам) со скоростью две трети скорости света, а потом развернуться и вернуться обратно.
Что мы увидим? Пока мы спали 12.5 секунд, второй кот побегал, вернулся и у него натикало всего 8.
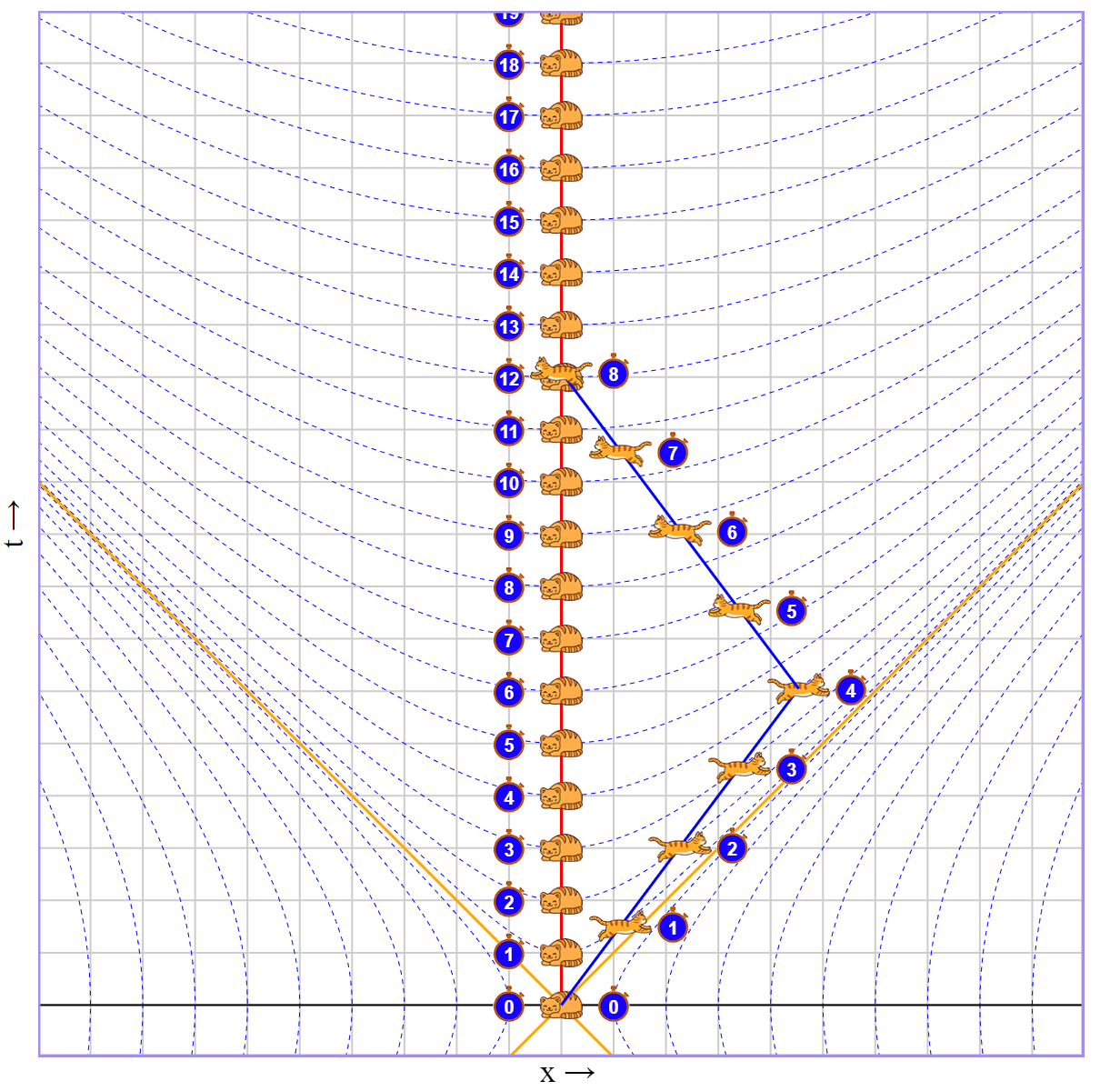
Да, это тот самый знаменитый парадокс близнецов. И чем быстрее и дольше второй кот бегает, тем менее постаревшим он вернется.
Кстати, этот эффект был напрямую проверен в 1971 году в эксперименте Ха́фелем и Ки́тингом. Упрощенно он выглядел так: Они взяли пару сверхточных атомных часов, синхронизировали их друг с другом, одни оставили на земле, а со вторыми совершили кругосветное путешествие на самолетах, после чего встретились в исходной точке. Самолет летит достаточно быстро, чтобы относительное замедление времени можно было измерить, и в итоге, на тех часах, что летали на самолете, натикало меньше времени в соответствии с предсказаниям теории относительности.
Но вернемся к близнецам и сути парадокса. Почему именно бегущий кот остался моложе, а не спящий? Ведь вроде бы мы можем перейти в систему отсчета бегущего и увидеть симметричную картину.
Парадокс близнецов
На самом деле ситуация не симметричная, т.к. именно бегущий кот менял направление движения. Давайте разобьем его путь на куски с постоянной скоростью и посмотрим на ситуацию в системе отсчета бегущего кота. А чтобы убедиться, что никакого обмана нет, обратите внимание, что при преобразованиях координат коты смещаются строго вдоль гипербол.
Для начала запустим кота вправо и перейдем в его систему отсчета. Затем перенесемся на 4 секунды вперед и опустим график вниз, чтобы второй этап начался с нуля. И перейдем в неподвижную систему отсчета где кот разворачивается и запускаем кота влево на 4 секунды:
Все сошлось! Никакого подвоха, спящий кот постарел сильнее. Чем быстрее кот убегает, тем дальше в будущем он окажется по возвращении. Так что, если вы очень ждете новый сезон сериала или выхода Nintendo Wii, вы знаете что делать.
Относительность одновременности
Вернемся к нашему кошачьему лежбищу.
Допустим, все коты в нулевой момент времени одновременно проснулись. Если мы будем смотреть на это неподвижно, то все будет хорошо. Но стоит нам начать двигаться, например, вправо со скоростью в половину скорости света, оказывается, что те коты, что слева еще не проснулись, а те что справа, проснулись уже давно.
Одновременность, оказывается, тоже относительна.
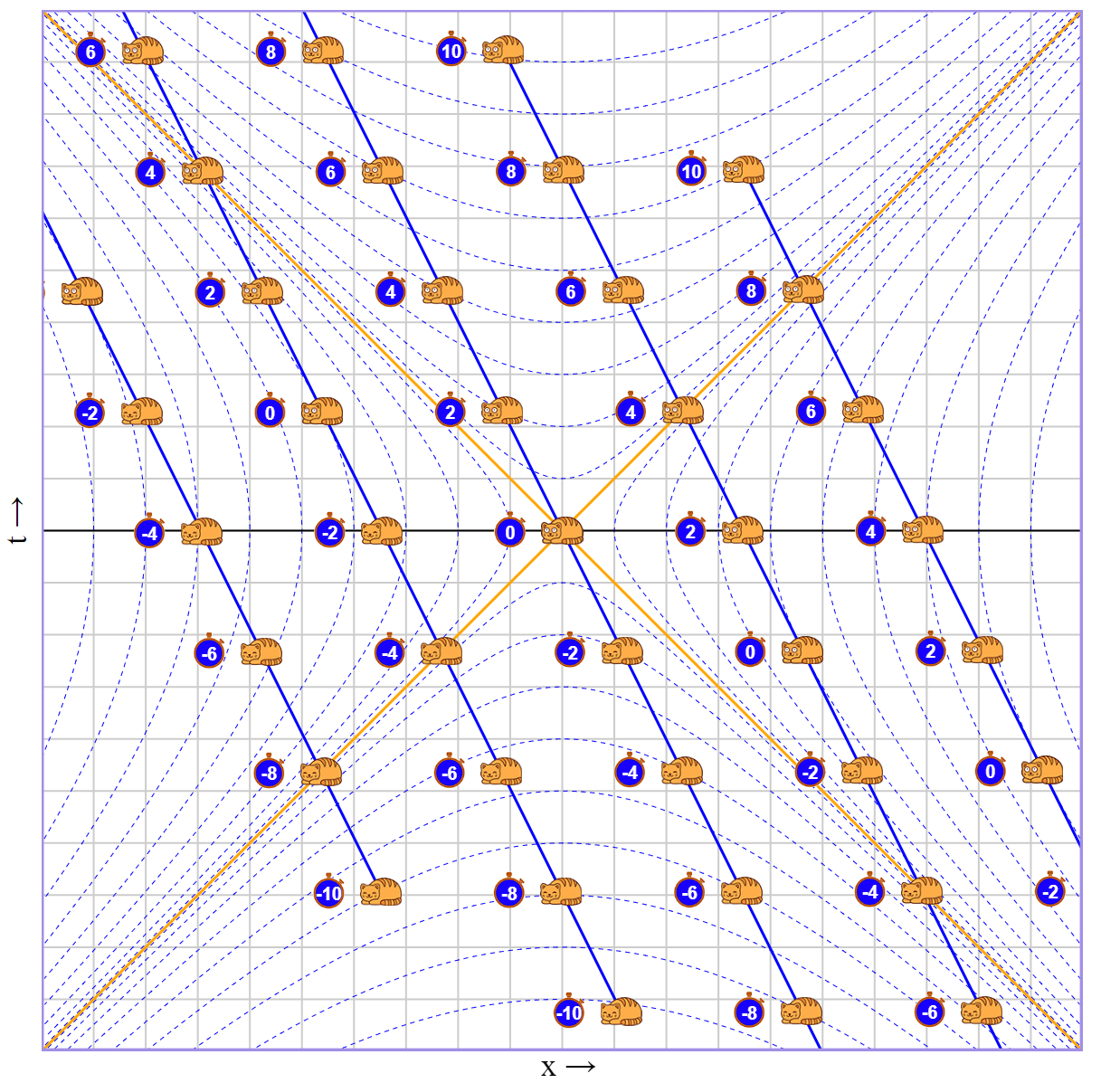
Если мы движемся вправо, то слева мы видим прошлое, и чем дальше, тем раньше. А справа - будущее. Получается, пространство и время буквально частично меняются местами (и это мы еще в общую теорию относительности не заходили).
Куда ни глянь, везде все становится относительным. Может хотя бы расстояния останутся абсолютными?

Сокращение длины
Возьмем очень длинную стрелу, положим ее перед собой и на оба ее конца повесим часы.

Теперь измерим длину этой стрелы. А что вообще такое длина? Это когда мы одновременно фиксируем положения концов и линейкой измеряем количество метров между ними. Думаю, вы уже догадались где тут будет подвох.
Измерим длину пока она неподвижна: Берем линейку и прикладываем ее вдоль горизонтальной оси. Вдоль стрелы укладывается ровно 4 узла сетки, значит ее длина 4 световые секунды.
А теперь запустим эту стрелу вправо со скоростью в половину скорости света:
Снова приложим линейку. На этот раз длина уже значительно меньше четырех. Но почему?

Обратите внимание на показания часов. Часы на правом конце показывают на две секунды меньше, чем на левом.То есть правый конец стрелы находится в прошлом относительно левого. Получается, левый конец стрелы буквально опережает правый, и из-за этого вся стрела становится короче. Но, опять же, это только для неподвижного наблюдателя так. Если бы мы двигались вместе со стрелой, то ее длина была бы нормальной.
В общем, длина оказалась тоже относительной. Кстати, это тоже не математический трюк, а вполне измеримая реальность с множеством примеров.
Возьмем два провода, расположим их параллельно и пустим по ним ток в одну сторону. В такой ситуации они начнут притягиваться. Раньше это объясняли тем, что движущиеся электроны в проводе создают магнитные поля, которые взаимодействуют, создавая силу Ампера, притягивающую провода друг к другу. Или отталкивающую, если токи текут в разные стороны.

А с теорией относительности оказалось, что никаких магнитных полей, сил Ампера и всего этого не нужно. Достаточно знать только то, что заряды одного знака отталкиваются, а разных знаков - притягиваются. И все.
Как только электроны начинают двигаться, для неподвижного наблюдателя расстояния между ними сокращаются. Сами электроны при этом тоже сплющиваются, но это не важно. Из-за этого их количество на единицу длины провода становится больше, и положительно заряженные атомы меди в одном проводе начинают сильнее притягиваться к электронам в другом проводе. А отталкивание между электронами разных проводов при этом не увеличится, ведь для них плотность электронов в чужом проводе не изменилась.
Ровно наоборот будет происходить если мы догоним электроны и посмотрим на летящие вниз атомы меди. Электроны думают, что это плотность положительных ионов меди стала выше. И результат тот же самый - провода притягиваются.
А если мы изменим направление тока в одном из проводов, то электроны станут двигаться относительно друг друга уже с двойной скоростью, и электроны одного провода будут видеть огромную плотность электронов в другом и станут отталкиваться гораздо сильнее, чем притягиваются к положительным ионам. В сумме окажется, что провода станут отталкиваться.
А уравнения описывающие процессы оказались точно такими же, как были с раньше с магнитными полями, только теперь никаких магнитных полей не нужно. Оказалось, что это просто электрическое поле так выглядит для подвижного наблюдателя. Эти рассуждения можно обобщить на любую систему с движущимися зарядами и полностью избавиться от такой сущности, как магнитное поле.
Путешествия "быстрее света"
А еще такие сокращения длин открывают для нас возможности перемещений на огромные расстояния за сколь угодно короткое время.
Допустим, на расстоянии 7 световых лет от нас расположена некоторая чужая галактика, куда мы очень хотим попасть (очень маленькая галактика). По “нормальной” логике, если мы будет лететь туда со скоростью в половину скорости света, то достигнем ее за 14 лет. И так на самом деле будет для неподвижного относительно галактики наблюдателя (спящего кота).
Но что почувствуем мы? Обратимся к диаграмме.
Чем выше наша скорость, тем ближе становится галактика (ведь длина сокращается).

Обратите внимание на синий отрезок. Его длина соответствует времени, через которое мы достигнем галактики (координата галактики станет равна нулю, т.е. сравняется с нашей). Чем выше наша скорость, тем короче отрезок. И при приближении к скорости света его длина стремится к нулю.
Последний кадр анимации соответствует скорости 96% от скорости света. При этом длина синего отрезка - 2 единицы (в этом случае это соответствует двум годам). Т.е. мы преодолеем 7 световых лет всего за два года. А если еще ускориться, то можно долететь хоть за одну секунду нашего локального времени.
Но есть одно “но”. Мы можем за секунду своего времени долететь до галактики на расстоянии миллион световых лет, но на самой галактики при этом пройдет миллион лет, ведь для стороннего наблюдателя мы будем лететь миллион лет со скоростью почти скорость света.
Этим эффектом объясняется почему короткоживущие частицы из космоса (например, мюоны, которые распадаются через пару микросекунд после рождения) способны пролететь огромное расстояние и достигнуть детекторов на поверхности земли, не успев распасться.
Заключение
Итак, подведем итоги.
Со времен Галилея в мире науки все было хорошо и понятно, пока в 19м веке не выяснилось, что измеренная скорость света не зависит от скорости наблюдателя, т.е. преобразования Галилея на свет просто не действуют. Для решения этой проблемы придумали выполнять преобразования координат не привычными сдвигами, а вращением в пространстве Минковского.
Это новое преобразование объясняло постоянство скорости света и не противоречило экспериментам на обычных скоростях.
Но побочным эффектом в таком пространстве стало замедлении времени, сокращение длин и другие чудеса, которые мало того, что подтвердились в эксперименте, так еще и много чего объяснили и предсказали.
Для закрепления давайте посмотрим на пример из жизни: Возьмем неподвижный корабль с двумя лампочками и попросим его мигать ими синхронно. И возьмем еще один такой же корабль, запустим его в полет и посмотрим на все это с земли.
Мы видим сразу несколько релятивистских эффектов:
Во-первых, на движущемся корабле лампочки мигают реже из-за эффекта замедления времени.
Во-вторых, эти лампочки стали красными, ведь замедление времени вызывает также и уменьшение частоты испускаемого света.
В третьих, левая лампочка на нем загорается раньше правой из-за того, что левая часть корабля находится в будущем относительно правой.
И в четвертых, длина корабля по оси движения уменьшилась по той же самой причине - левая часть догоняет правую, так как она в будущем относительно правой.
Ну а в системе отсчета движущегося корабля все происходит наоборот:
Тема оказалась для меня настолько интересной, что я решил изложить материал в виде ютуб ролика для тех, кому удобнее воспринимать информацию в формате видео. И даже создал экспериментальный канал (это видео в нем первое). Буду рад подпискам для мотивировации к созданию новых статей и видео.
Надеюсь, теперь вы по настоящему поняли специальную теорию относительности. А если у вас остались вопросы, буду рад ответить на них в комментариях.
Визуализатор
Для иллюстраций и анимаций я написал интерактивный браузерный визуализатор, где можно двигать ползунки, менять режимы и наблюдать за преобразованиями Лоренца.
Визуализатор: https://dudarion.github.io/Interactive-Minkowski-diagram/
Проект на гитхабе: https://github.com/Dudarion/Interactive-Minkowski-diagram
Сам я железячник/сишник/питонист, и этот проект стал моим первым знакомством с js. Поэтому прошу сильно не пинать за излишнюю красоту кода.
Спасибо за внимание!