В отличие от окружающего нас мира, в котором всё конечно, в математике мы часто сталкиваемся с бесконечными объектами. Например, бесконечны множества целых, рациональных, алгебраических, конструктивных или действительных чисел. На лекции мы рассмотрим задачи, в которых проявляются некоторые принципы работы с бесконечными множествами. Иногда эти принципы сильно отличаются от тех, к которым мы привыкли в случае «конечного» мира.
Представим себе гипотетический отель с бесконечным количеством номеров. Все номера в отеле уже заселены. но в определенный момент в отель приезжает еще один постоялец. Несмотря на то, что в каждом номере отеля уже есть хотя бы один жилец, комнату для нового все же можно найти. Ведь наш отель бесконечен, и если попросить всех постояльцев переселиться на один номер дальше, самый первый номер окажется свободен. И даже если приедет несколько новых постояльцев, путем серии подобных переселений, можно будет найти место и для них.
А теперь представим, что у нас три таких гильберотовых отеля. Два из них закрываются на ремонт, и постояльцев нужно расселить в один оставшийся. Даже такой необычный случай не должен вызвать никаких проблем, всем постояльцам найдется место в третьем бесконечном отеле. Например, мы можем последовательно расселять постояльцев из двух отелей по четным и нечетным номерам соответственно.
Представим еще более странную ситуацию: бесконечное количество гильбертовых отелей закрывается на ремонт, и нам нужно расселить всех их постояльцев в один бесконечный отель. Если мы воспользуемся приемом из предыдущего примера, но будем расселять постояльцев последовательно по диагонали, рано или поздно нам удастся распределить всех.
Попробуем формализовать рассмотренные нами только что задачи с точки зрения теории множеств. Что мы по сути сейчас делали? Мы нумеровали комнаты отеля. Такая ситуация в математике называется счетным множеством: бесконечное множество K, которое можено перенумеровать. Бесконечное множество называется счетным, если существует взаимно однозначное соответствие между элементами множества K и натуральными числами {1, 2, …}. Формальное представление рассмотренных нами задач выглядит следующим образом:
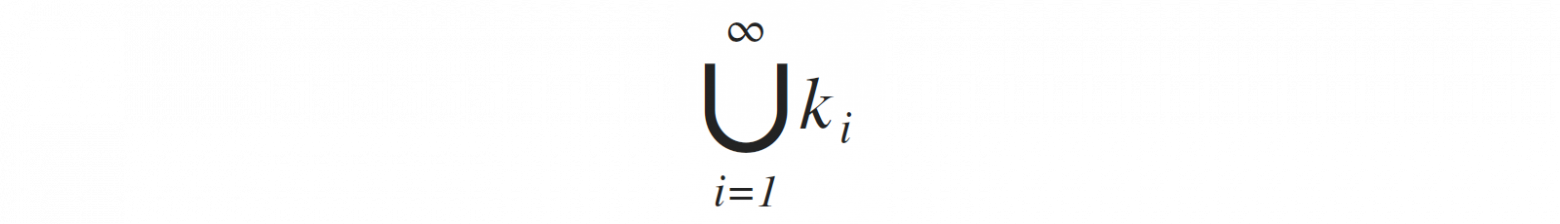
Но перейдем к более привычным для нас множествам – числовым. И начнем с натуральных чисел. Очевидно, что множество натуральных чисел (ℕ) счетное просто по определению. Если мы добавим к натуральным числам ноль и отрицательные числа, мы получим множество целых чисел. Счетное ли это множество? Мы уже говорили выше, что если объединить два счетных множества, результат также будет счетным множеством. От добавления 0 множество не потеряет свойства быть счетным.
Далее рассмотрим рациональные числа. Это множество чисел, представимых в виде m/n, где m – целое число, а n – натуральное:

Таким образом, рациональные числа представляют собой счетное число счетных множеств и при объединении также станут счетным множеством.
Алгебраические числа – это множество корней многочленов с целыми коэффициентами. Будет ли это множество счетным? Множества корней многочленов разных степеней являются счетными множествами, а значит, результат их объединения также будет счетным множеством. Из этого следует, что множество алгебраических чисел (𝔸) – это счетное множество.
Существуют так называемые трансцендентные числа: в это множество (𝕀) входят действительные (ℝ), но не алгебраические (𝔸) числа. К этому множеству относятся числа e, π и т.д.
Раз уж мы упомянули действительные числа, остановимся на них подробнее, тем более, что как раз их множество счетным не является, что мы сейчас и докажем. И для этого нужно доказать что множество бесконечных десятичных дробей несчетно. Для простоты представим, что после запятой у нас могут быть только нули и единицы:

Допустим, что у нас есть бесконечная таблица, в которой пронумерованы все числа, указанного нами вида.
Докажем, что такой таблицы существовать не может, сконструируем такую дробь, встретить которую в этой таблице невозможно:
0,x1, x2, x3, x4, x x5 …
Где x1≠a1, x2≠b2, x3≠c3 и т.д. Называется это канторовым диагональным процессом, он приводит нас к числу, которого нет в нашей таблице. А значит, множество у нас несчетное.
Посмотрев лекцию до конца, вы узнаете какие бывают задачи, связанные с бесконечными множествами, и как они решаются.
Гильбертов отель
Представим себе гипотетический отель с бесконечным количеством номеров. Все номера в отеле уже заселены. но в определенный момент в отель приезжает еще один постоялец. Несмотря на то, что в каждом номере отеля уже есть хотя бы один жилец, комнату для нового все же можно найти. Ведь наш отель бесконечен, и если попросить всех постояльцев переселиться на один номер дальше, самый первый номер окажется свободен. И даже если приедет несколько новых постояльцев, путем серии подобных переселений, можно будет найти место и для них.
А теперь представим, что у нас три таких гильберотовых отеля. Два из них закрываются на ремонт, и постояльцев нужно расселить в один оставшийся. Даже такой необычный случай не должен вызвать никаких проблем, всем постояльцам найдется место в третьем бесконечном отеле. Например, мы можем последовательно расселять постояльцев из двух отелей по четным и нечетным номерам соответственно.
Представим еще более странную ситуацию: бесконечное количество гильбертовых отелей закрывается на ремонт, и нам нужно расселить всех их постояльцев в один бесконечный отель. Если мы воспользуемся приемом из предыдущего примера, но будем расселять постояльцев последовательно по диагонали, рано или поздно нам удастся распределить всех.
Попробуем формализовать рассмотренные нами только что задачи с точки зрения теории множеств. Что мы по сути сейчас делали? Мы нумеровали комнаты отеля. Такая ситуация в математике называется счетным множеством: бесконечное множество K, которое можено перенумеровать. Бесконечное множество называется счетным, если существует взаимно однозначное соответствие между элементами множества K и натуральными числами {1, 2, …}. Формальное представление рассмотренных нами задач выглядит следующим образом:
- K – счетное множество, следовательно, K∪{a} также будет счетным множеством.
- К1, K2 – счетные множества, следовательно, К1∪K2 будет счетным множеством.
- K1, K2, K3, K4, … – счетные множества, следовательно, объединенное множество также будет счетным:
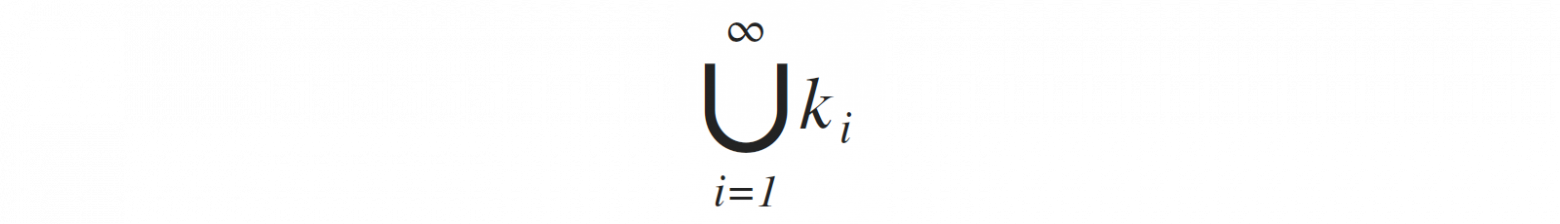
Счетные и несчетные множества
Но перейдем к более привычным для нас множествам – числовым. И начнем с натуральных чисел. Очевидно, что множество натуральных чисел (ℕ) счетное просто по определению. Если мы добавим к натуральным числам ноль и отрицательные числа, мы получим множество целых чисел. Счетное ли это множество? Мы уже говорили выше, что если объединить два счетных множества, результат также будет счетным множеством. От добавления 0 множество не потеряет свойства быть счетным.
Далее рассмотрим рациональные числа. Это множество чисел, представимых в виде m/n, где m – целое число, а n – натуральное:

Таким образом, рациональные числа представляют собой счетное число счетных множеств и при объединении также станут счетным множеством.
Алгебраические числа – это множество корней многочленов с целыми коэффициентами. Будет ли это множество счетным? Множества корней многочленов разных степеней являются счетными множествами, а значит, результат их объединения также будет счетным множеством. Из этого следует, что множество алгебраических чисел (𝔸) – это счетное множество.
Существуют так называемые трансцендентные числа: в это множество (𝕀) входят действительные (ℝ), но не алгебраические (𝔸) числа. К этому множеству относятся числа e, π и т.д.
Раз уж мы упомянули действительные числа, остановимся на них подробнее, тем более, что как раз их множество счетным не является, что мы сейчас и докажем. И для этого нужно доказать что множество бесконечных десятичных дробей несчетно. Для простоты представим, что после запятой у нас могут быть только нули и единицы:

Допустим, что у нас есть бесконечная таблица, в которой пронумерованы все числа, указанного нами вида.
| 0,a1, a2, a3, a4, a5 … |
| 0,b1, b2, b3, b4, b5 … |
| 0,c1, c2, c3, c4, c5 … |
| 0,d1, d2, d3, d4, d5 … |
| ... |
| ... |
| ... |
Докажем, что такой таблицы существовать не может, сконструируем такую дробь, встретить которую в этой таблице невозможно:
0,x1, x2, x3, x4, x x5 …
Где x1≠a1, x2≠b2, x3≠c3 и т.д. Называется это канторовым диагональным процессом, он приводит нас к числу, которого нет в нашей таблице. А значит, множество у нас несчетное.
Посмотрев лекцию до конца, вы узнаете какие бывают задачи, связанные с бесконечными множествами, и как они решаются.
