В компании Intel разрабатывают не только ПО для «внешних» потребителей — пишутся и программы, которые используются только внутри Intel. Среди них довольно много средств для численного моделирования различных физических процессов, протекающих при изготовлении процессоров — ведь именно последние и являются основной продукцией Интела. В этих программах, конечно, широко используются различные методы вычислительной математики и физики.
Вот некоторое время назад мне понадобилось программно решать одно уравнение методом Ньютона. Казалось бы, все просто, но для этого надо уметь вычислять производную левой части уравнения. Эта левая часть у меня была довольно сложная — даже просто вычисление ее значений в программе было разбросано по нескольким функциям, — и перспектива вычислять производную на бумажке меня не радовала. Перспектива воспользоваться каким-нибудь пакетом символьных вычислений меня радовала не больше — перенабирать все формулы, содержащие к тому же несколько частных случаев, далеко не очень приятно. Вариант вычислять производную численно как разность значений функции в двух соседних точках, деленную на соответствующее приращение независимой переменной, чреват потерей точности и вообще необходимостью подбирать подходящее приращение этой переменной.
Подумав некоторое время, я применил следующий подход. Потом я узнал, что он называется «автоматические дифференцирование», для него существует довольно обширная литература на английском, и ряд библиотек — но на русском я нашел только некоторые научные статьи про применение этого метода, и пост на Хабрахабре, в котором все рассказывается через смесь дуальных и комплексных чисел, и понять который с ходу, на мой взгляд, тяжело. С другой стороны, для понимания и практического применения автоматического дифференцирования не нужны никакие дуальные числа, и этот подход я тут и изложу.
Итак, пусть у нас есть какая-нибудь функция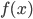 . Пусть мы в некоторой точке
. Пусть мы в некоторой точке 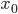 знаем ее значение
знаем ее значение 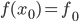 , и знаем значение ее производной
, и знаем значение ее производной  . Мы знаем только только два числа:
. Мы знаем только только два числа: 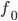 и
и  , больше ничего знать нам не надо — ни выражения для
, больше ничего знать нам не надо — ни выражения для 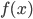 , ни даже значения
, ни даже значения 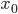 . Рассмотрим функцию
. Рассмотрим функцию 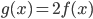 и зададимся вопросом: чему равно ее значение и значение ее производной в точке
и зададимся вопросом: чему равно ее значение и значение ее производной в точке 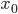 ? Очевидно:
? Очевидно: 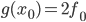 и
и 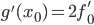 . Обратите внимание, что в правой части здесь стоят только те числа, которые мы знаем.
. Обратите внимание, что в правой части здесь стоят только те числа, которые мы знаем.
Вопрос чуть сложнее: рассмотрим функцию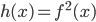 , и зададимся про нее тем же вопросом. Несложно видеть, что и в этом случае мы легко находим
, и зададимся про нее тем же вопросом. Несложно видеть, что и в этом случае мы легко находим 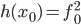 , и
, и 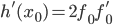 . Аналогично, для
. Аналогично, для 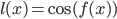 имеем
имеем 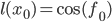 и
и 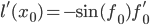 . И так далее: для любой элементарной функции, примененой к
. И так далее: для любой элементарной функции, примененой к 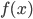 , мы можем вычислить значение и производную, используя только два числа:
, мы можем вычислить значение и производную, используя только два числа: 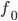 и
и  .
.
Далее, пусть есть еще какая-нибудь функция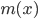 , и про нее мы тоже знаем только два числа:
, и про нее мы тоже знаем только два числа: 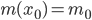 и
и 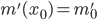 . Тогда для функции
. Тогда для функции 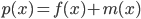 мы столь же легко можем вычислить и значение, и производную в той же точке; и аналогично для любой бинарной операции. Например, для умножения имеем: если
мы столь же легко можем вычислить и значение, и производную в той же точке; и аналогично для любой бинарной операции. Например, для умножения имеем: если 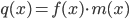 , то
, то 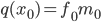 и
и 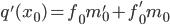 .
.
Таким образом, мы можем свободно выполнять любые операции над парами чисел (значение функции, значение ее производной), и никакой дополнительной информации нам не понадобится. Если в некоторой точке мы знаем значения некоторых «базовых» функций и значения их производных, то для любой сложной функции, определяемой через эти «базовые», мы можем автоматически вычислить и ее значение, и значение ее производной.
Легко пишется класс, который реализует такую арифметику:
Теперь, если у нас есть код, вычисляющий некоторую функцию, то достаточно просто заменить везде , и, во-вторых, собственно сама
, и, во-вторых, собственно сама  . Любую константу
. Любую константу  , не зависящую от
, не зависящую от  , надо, конечно, заменить на
, надо, конечно, заменить на 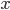 — на
— на 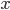 , для которого мы вычисляем функцию. В реальной программе, скорее всего, соответствующая переменная будет называться тоже
, для которого мы вычисляем функцию. В реальной программе, скорее всего, соответствующая переменная будет называться тоже
Вот пример вычисления функции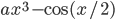 вместе с ее производной:
вместе с ее производной:
Вот пример кода, решающего уравнение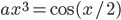 методом Ньютона (здесь я еще, естественно, операторы сделал глобальными, чтобы работало
методом Ньютона (здесь я еще, естественно, операторы сделал глобальными, чтобы работало
Все это будет работать, даже если у нас в коде есть не очень сложные ветвления, циклы, вызовы других функций и т.д. — главное везде все промежуточные переменные (и в том числе результаты промежуточных функций) сделать
Конечно, можно придумать и такую функцию, для которой такой подход работать не будет — вдруг вам придет в голову вычислять функцию
Напоследок несколько слов об обобщениях этого подхода. На случай нескольких независимых переменных все обобщается очевидным образом: просто будем хранить соответствующее количество производных. Полезно, наверное, класс
Также несложно все обобщить и на случай производных высших степеней. Я этого сам не делал, но с ходу мне кажется, что это не очень сложно, хотя немного подумать придется. Во-первых, конечно, можно вручную для каждого оператора и элементарной функции вывести формулы пересчета всех производных до нужной степени, и забить эти формулы в код. Во-вторых, можно все-таки думать в терминах дуальных чисел (см. по ссылкам из начала поста), или (как, на мой взгляд, проще), в терминах разложения в ряд Тейлора: если мы храним не производные, а коэффициенты разложения в ряд, то нам надо просто уметь выполнять операции над рядами, что довольно просто.
В-третьих, есть еще один интересный подход, который я краем глаза видел в одном из open-source кодов для автоматического дифференцирования (см. по ссылкам из википедии). Можно сделать класс
Вот некоторое время назад мне понадобилось программно решать одно уравнение методом Ньютона. Казалось бы, все просто, но для этого надо уметь вычислять производную левой части уравнения. Эта левая часть у меня была довольно сложная — даже просто вычисление ее значений в программе было разбросано по нескольким функциям, — и перспектива вычислять производную на бумажке меня не радовала. Перспектива воспользоваться каким-нибудь пакетом символьных вычислений меня радовала не больше — перенабирать все формулы, содержащие к тому же несколько частных случаев, далеко не очень приятно. Вариант вычислять производную численно как разность значений функции в двух соседних точках, деленную на соответствующее приращение независимой переменной, чреват потерей точности и вообще необходимостью подбирать подходящее приращение этой переменной.
Подумав некоторое время, я применил следующий подход. Потом я узнал, что он называется «автоматические дифференцирование», для него существует довольно обширная литература на английском, и ряд библиотек — но на русском я нашел только некоторые научные статьи про применение этого метода, и пост на Хабрахабре, в котором все рассказывается через смесь дуальных и комплексных чисел, и понять который с ходу, на мой взгляд, тяжело. С другой стороны, для понимания и практического применения автоматического дифференцирования не нужны никакие дуальные числа, и этот подход я тут и изложу.
Простые соображения
Итак, пусть у нас есть какая-нибудь функция
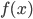 . Пусть мы в некоторой точке
. Пусть мы в некоторой точке 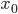 знаем ее значение
знаем ее значение 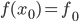 , и знаем значение ее производной
, и знаем значение ее производной 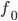 и
и  , больше ничего знать нам не надо — ни выражения для
, больше ничего знать нам не надо — ни выражения для 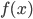 , ни даже значения
, ни даже значения 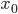 . Рассмотрим функцию
. Рассмотрим функцию 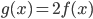 и зададимся вопросом: чему равно ее значение и значение ее производной в точке
и зададимся вопросом: чему равно ее значение и значение ее производной в точке 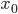 ? Очевидно:
? Очевидно: 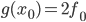 и
и 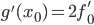 . Обратите внимание, что в правой части здесь стоят только те числа, которые мы знаем.
. Обратите внимание, что в правой части здесь стоят только те числа, которые мы знаем.Вопрос чуть сложнее: рассмотрим функцию
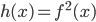 , и зададимся про нее тем же вопросом. Несложно видеть, что и в этом случае мы легко находим
, и зададимся про нее тем же вопросом. Несложно видеть, что и в этом случае мы легко находим 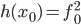 , и
, и 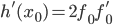 . Аналогично, для
. Аналогично, для 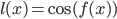 имеем
имеем 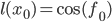 и
и 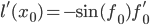 . И так далее: для любой элементарной функции, примененой к
. И так далее: для любой элементарной функции, примененой к 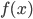 , мы можем вычислить значение и производную, используя только два числа:
, мы можем вычислить значение и производную, используя только два числа: 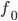 и
и  .
.Далее, пусть есть еще какая-нибудь функция
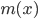 , и про нее мы тоже знаем только два числа:
, и про нее мы тоже знаем только два числа: 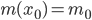 и
и 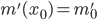 . Тогда для функции
. Тогда для функции 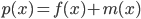 мы столь же легко можем вычислить и значение, и производную в той же точке; и аналогично для любой бинарной операции. Например, для умножения имеем: если
мы столь же легко можем вычислить и значение, и производную в той же точке; и аналогично для любой бинарной операции. Например, для умножения имеем: если 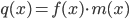 , то
, то 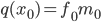 и
и 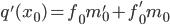 .
.Таким образом, мы можем свободно выполнять любые операции над парами чисел (значение функции, значение ее производной), и никакой дополнительной информации нам не понадобится. Если в некоторой точке мы знаем значения некоторых «базовых» функций и значения их производных, то для любой сложной функции, определяемой через эти «базовые», мы можем автоматически вычислить и ее значение, и значение ее производной.
Код
Легко пишется класс, который реализует такую арифметику:
class Derivable {
double val, deriv;
public:
Derivable(double _val, double _deriv) : val(_val), deriv(_deriv) {}
double getValue() {return val;}
double getDerivative() {return deriv;}
Derivable operator+(Derivable f) {
return Derivable(val + f.val, deriv + f.deriv);
}
Derivable operator-(Derivable f) {
return Derivable(val - f.val, deriv - f.deriv);
}
Derivable operator*(Derivable f) {
return Derivable(val * f.val, deriv * f.val + val * f.deriv);
}
Derivable operator/(Derivable f) {
return Derivable(val / f.val, (deriv * f.val - val * f.deriv) / f.val / f.val);
}
friend Derivable cos(Derivable f);
};
Derivable cos(Derivable f) {
return Derivable(cos(f.val), -sin(f.val)*f.deriv);
}
Теперь, если у нас есть код, вычисляющий некоторую функцию, то достаточно просто заменить везде
double на Derivable — и получится код, вычисляющий ту же функцию вместе с ее производной. Правда, конечно, возникнет вопрос: с чего начать? Мы пока умеем по Derivable получать новые Derivable, но откуда взять самые первые Derivable? На самом деле, все понятно. В выражения для нашей функции входят, во-первых, различные константы, не зависящие от 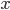 , и, во-вторых, собственно сама
, и, во-вторых, собственно сама 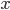 . Любую константу
. Любую константу  , не зависящую от
, не зависящую от 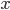 , надо, конечно, заменить на
, надо, конечно, заменить на Derivable(c, 0); а вхождения собственно переменной 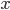 — на
— на Derivable(x0, 1). (Здесь для понятности x0 обозначает то значение 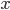 , для которого мы вычисляем функцию. В реальной программе, скорее всего, соответствующая переменная будет называться тоже
, для которого мы вычисляем функцию. В реальной программе, скорее всего, соответствующая переменная будет называться тоже x).Вот пример вычисления функции
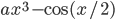 вместе с ее производной:
вместе с ее производной:Derivable f(double x, double a) {
Derivable xd(x, 1);
Derivable ad(a, 0);
Derivable two(2, 0);
return ad*xd*xd*xd - cos(xd/two);
}
Derivable(double c): val(c), deriv(0) {}
static Derivable IndependendVariable(double x) { return Derivable(x,1); }
Derivable f(double x, double a) {
Derivable xd = Derivable::IndependendVariable(x);
return xd*xd*xd*a - cos(xd/2);
}
Вот пример кода, решающего уравнение
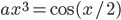 методом Ньютона (здесь я еще, естественно, операторы сделал глобальными, чтобы работало
методом Ньютона (здесь я еще, естественно, операторы сделал глобальными, чтобы работало a*xd; выше они члены класса только для того, чтобы не загромождать код). Если вы захотите изменить решаемое уравнение, вам надо поменять код функции f и всё; производная будет автоматически вычисляться верно. (Конечно, в данном примере, может быть, проще было бы посчитать производную руками, потому что функция простая, — но как только уравнения у вас становятся более сложными, возможность не думать о коде вычисления производной оказывается очень удобной.)Все это будет работать, даже если у нас в коде есть не очень сложные ветвления, циклы, вызовы других функций и т.д. — главное везде все промежуточные переменные (и в том числе результаты промежуточных функций) сделать
Derivable, остальной код даже менять не потребуется! Конечно, можно придумать и такую функцию, для которой такой подход работать не будет — вдруг вам придет в голову вычислять функцию
f методом Монте-Карло? — но все равно область применения автоматического дифференцирования весьма широка. (А потом, если уж вы и правда вычисляете свою функцию методом Монте-Карло, то как вы вообще представляете себе ее производную?)Обобщения
Напоследок несколько слов об обобщениях этого подхода. На случай нескольких независимых переменных все обобщается очевидным образом: просто будем хранить соответствующее количество производных. Полезно, наверное, класс
Derivable сделать шаблонным, принимающим в качестве параметра шаблона количество независимых переменных.Также несложно все обобщить и на случай производных высших степеней. Я этого сам не делал, но с ходу мне кажется, что это не очень сложно, хотя немного подумать придется. Во-первых, конечно, можно вручную для каждого оператора и элементарной функции вывести формулы пересчета всех производных до нужной степени, и забить эти формулы в код. Во-вторых, можно все-таки думать в терминах дуальных чисел (см. по ссылкам из начала поста), или (как, на мой взгляд, проще), в терминах разложения в ряд Тейлора: если мы храним не производные, а коэффициенты разложения в ряд, то нам надо просто уметь выполнять операции над рядами, что довольно просто.
В-третьих, есть еще один интересный подход, который я краем глаза видел в одном из open-source кодов для автоматического дифференцирования (см. по ссылкам из википедии). Можно сделать класс
Derivable шаблонным, принимающим в качестве параметра шаблона тип данных для значений функции и производной (т.е. чтобы надо было писать Derivable и т.п.; запись Derivable будет соответствовать функции 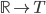 ). Тогда если написать Derivable<Derivable >, то не получатся ли вторые производные автоматически? Эдакое применение автоматического дифференцирования к автоматическому дифференцированию. Правда, при таким подходе делается лишняя работа: если расписать, например, какой получится оператор умножения, то видно, что всё получится правильно, но первая производная будет вычисляться дважды. Кстати, при правильной инициализации начальных переменных объекты типа Derivable<Derivable >, видимо, можно применять и для вычисления производных по нескольким независимым переменным.
). Тогда если написать Derivable<Derivable >, то не получатся ли вторые производные автоматически? Эдакое применение автоматического дифференцирования к автоматическому дифференцированию. Правда, при таким подходе делается лишняя работа: если расписать, например, какой получится оператор умножения, то видно, что всё получится правильно, но первая производная будет вычисляться дважды. Кстати, при правильной инициализации начальных переменных объекты типа Derivable<Derivable >, видимо, можно применять и для вычисления производных по нескольким независимым переменным.
Другие реализации
Отмечу, что описанный выше подход с перегрузкой операторов не является единственным возможным; даже различают «forward» и «reverse» реализации (подробнее см. в википедии и по ссылкам оттуда). В частности, по-видимому, многие коды, на которые приведены ссылки в википедии, используют несколько более общие подходы — но я их смотрел только очень поверхностно.
Ссылки
http://habrahabr.ru/post/63055/
http://en.wikipedia.org/wiki/Automatic_differentiation, со ссылками на множество реализаций
http://www.coin-or.org/CppAD/Doc/mul_level.htm (про конструкцию вида Derivable<Derivable >)