
Я очень часто по работе слышу вопрос, задаваемый из, большей частью, академической среды, ввиду огромного количества выполняемых вычислений именно там: «Почему наши результаты разные от запуска к запуску одного и того же приложения? Мы же ничего не меняем в нем». Стоит отметить, разговор про это уже был, но лишь частично отвечающий на вопрос. Попробую рассказать про эту проблему ещё чуть-чуть.
Почему мы можем видеть следующую картину на одной и той же системе:
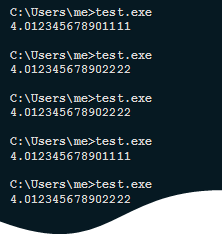
Или, скажем, следующую, на двух разных машинах:

Основная причина, из-за которой всё это происходит, состоит в том, что закон ассоциативности, который в математике всегда работает, в вычислениях на машинах с ограниченной разрядной сеткой невыполним, то есть (a+b)+c не равно a+(b+c).
По этой теме много интересного можно найти в статье What Every Computer Scientist Should Know About Floating-Point Arithmetic, автор David Goldberg. Я же приведу простой наглядный пример, когда в вычислениях встречаются очень маленькие и относительно большие числа:

Вроде бы пока всё ожидаемо, если мы считаем как математики. Теперь предположим, что мы работаем с числами с одинарной точностью, и сложим маленькое число с большим:

С точки зрения машинной арифметики, мы получили правильный результат, согласно стандарту IEEE 754. И следующий результат тоже верен:
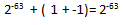
Именно отсюда и начинают вылезать все проблемы. Ведь компилятор вполне может оптимизировать наш код так, что порядок сложений в выражениях поменяется, да и ещё много чего другого. И здесь помогут опции –fp-model, про которые я уже подробно рассказывал.
Вот только не всё зависит от компилятора. Помните, оригинальный вопрос то звучал так, что вроде бы ничего не менялось в коде, а значит его не «пересобирали», но результаты всё равно разные.
Так вот, на сцену выходят другие факторы. Для последовательного приложения, равно как и для параллельного, одним из важных аспектов для получения воспроизводимых результатов является выравнивание данных. Кстати, на производительность оно так же имеет огромное влияние. И если данные у нас в коде никто не выравнивал, то в циклах, которые векторизованы, разное количество итераций будут распознаны как пролог, ядро цикла и эпилог, а, соответственно, и порядок вычислений будет изменён. Для того, чтобы предотвратить подобные проблемы, можно пойти двумя путями:
1) Сохранить оптимизации, но при этом явно выравнивать данные, например, используя _mm_malloc() и _mm_free(). В Фортране есть директива !DIR$ ATTRIBUTES ALIGN:64 :: arrayname, а так же компиляторная опция -align array64byte
2) Отказаться от векторизации редукций и ряда других оптимизаций, используя опцию –fp-model precise, что повлечет за собой потерю в производительности.
Отлично! Допустим, что мы скомпилировали наш код с –fp-model precise, но результаты до сих не отличаются постоянством. Что же теперь не так? На самом деле, есть ещё ряд причин.
Во-первых, если наше приложение параллельно, то это число потоков. Скажем, редукции в OpenMP никоим образом не затрагиваются опциями компилятора. Таким образом, изменяя число потоков, а на разных системах оно вполне может быть разным по умолчанию, мы неявно изменяем порядок сложений в редукциях (равно как и их количество). Больше того, никто и не говорит о том, что промежуточные суммы в OpenMP будут суммироваться в одинаковой последовательности от запуска к запуску, соответственно, даже при одинаковом количестве потоков мы можем получать разный порядок суммирования, а значит, и разные результаты. Кстати, это свойственно и icc, и gcc. При этом результаты вполне могут быть более точными, чем в последовательной версии редукции.
Нам нужно контролировать это самим, и в компиляторе Intel, начиная с версии 13.0, есть переменная окружения, которая позволяет выполнять детерминированные редукции. Это KMP_DETERMINISTIC_REDUCTION. Выставляем её в yes, и можем быть спокойными, но только при условии, что мы используем статическое распределение работы между потоками (static scheduling), и число потоков неизменно.
Если же мы используем Intel Threading Building Blocks, то и там мы можем контролировать редукции, через вызов функции parallel_deterministic_reduce(). Кстати, в Intel TBB нет зависимости от числа потоков, и результат может отличаться от последовательной версии редукции.
Хорошо. Мы добавили и это, но опять не помогает.
Тогда есть подозрение, что используются библиотеки, которые знать не знают про ваше стремление к «постоянности». Хочу сначала обратить внимание на вызовы математических функций. Опция –fp-model позволяет добиться консистентности вызовов функций, но для получения идентичных результатов на разных архитектурах (в том числе и не Интеловских), рекомендуется использовать ключ –fimf-arch-consistency.
Более «мощный» пример — использование библиотеки Intel Math Kernel Library, которая по умолчанию не ориентирована на воспроизводимость результатов, но этого можно добиться, используя дополнительные настройки, и при соблюдении ряда ограничений.
Например, при одинаковом количестве потоков, статическом планировщике (OMP_SCHEDULE=static, выставлен по умолчанию), одной и той же ОС и архитектуре, можно получать воспроизводимые результаты. Эта возможность называется в MKL Conditional Numerical Reproducibility. Я думаю понятно, почему она условная. Кстати, раньше так же было требование к выравниванию данных, но в последней версии инженеры чего-то «нашаманили», и об этом условии можно больше не заботиться при работе с MKL. Так вот при соблюдении этих требований, выставляя переменную окружения MKL_CBWR_BRANCH (например, в значение «COMPATIBLE»), или вызывая функцию mkl_cbwr_set(MKL_CBWR_COMPATIBLE) в коде, мы получим долгожданную «стабильность».
Таким образом, работая с большим количеством вычислений мы должны понимать, что добиться «постоянных»результатов возможно, но лишь с соблюдением ряда условий, о которых мы говорили. Почти во всех инструментах сегодня существует способ контролировать этот вопрос, нужно быть внимательным и выставлять нужные настройки и опции. Ну и ещё – часто причина банальна, и кроется в обычных ошибках. Иногда интересно видеть код, вычисляющий серьёзные научные формулы, используя, скажем, неинициализированные переменные. А потом мы удивляемся, чего это очередная ракета полетела не туда. Будьте внимательны при написании кода и используйте правильные средства для его создания и отладки.
Кстати, такой вопрос. Почему же в примере на системах с разными Xeon'ами (картинка наверху), мы получали разные результаты? Я про это явно так и не написал, было бы интересно услышать ваши идеи.