
Данная публикация является переводом первой части статьи Characterization and Optimization Methodology Applied to Stencil Computations инженеров компании Intel. Эта часть посвящена анализу производительности и построению roofline модели на примере довольно распространенного вычислительного ядра, которая позволяет оценить перспективы оптимизации приложения на данной платформе.
В следующей части будет описано, какие оптимизации были применены для того, чтобы приблизиться к ожидаемому значению производительности. Техники оптимизации, описанные в данной статье, включают, к примеру:
- масштабируемое распараллеливание (collaborative thread blocking)
- увеличение пропускной способности памяти (cache blocking, переиспользование регистров)
- увеличение производительности процессора (векторизация, переразбиение циклов).
В третьей части статьи будет описан алгоритм, позволяющий автоматически подобрать оптимальные параметры запуска и построения приложения. Эти параметры обычно связаны с изменениями исходного кода программы (например, loop blocking значения), с параметрами для компилятора (например, фактор развертки цикла) и характеристиками вычислительной системы (например, размеры кэшей). Получившийся алгоритм оказался быстрее, чем традиционные тяжеловесные техники поиска. Начиная с простейшей реализации и до самой оптимизированной, было получено 6-кратное улучшение производительности на процессоре Intel Xeon E5-2697v2 и примерно 3-кратное на сопроцессорах Intel Xeon Phi первого поколения. В дополнение к этому, приведенная методология автоматического тюнинга выбирает оптимальные параметры запуска для любого набора входных данных.
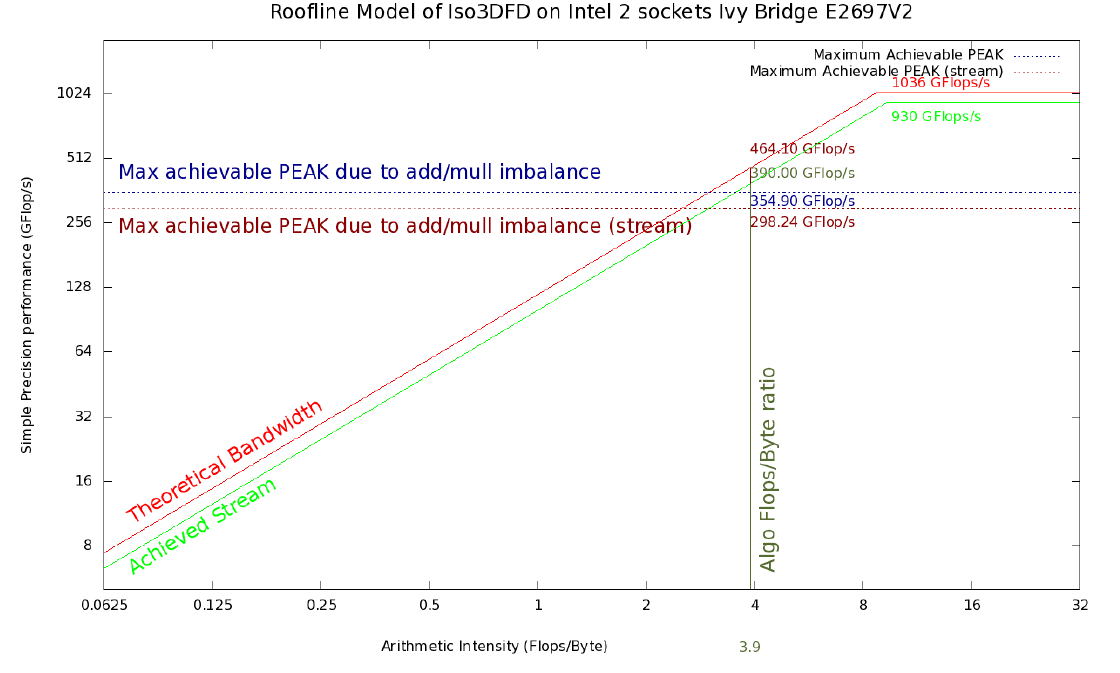
Рисунок 1. Roofline модель Iso3DFD для Ivy Bridge 2S E5-2697 v2. Красная и светло-зеленые линии обозначают верхний теоретический и достижимый предел на текущей платформе соответственно. Горизонтальная синяя линия отражает максимально достижимые значения пропускной способности памяти принимая во внимание определенный дисбаланс сложений и умножений (#ADD;#MUL) и усредненные с помощью Stream triad бенчмарка (горизонтальная коричневая линия). Вертикальная темно-зеленая линия соответствует арифметической интенсивности для ядра Iso3DFD алгоритма. Пересечения с остальными линиями дают соответствующие достижимые пределы.
Краткий обзор
Статья описывает характеризацию (прим. переводчика — характеризация — выявление характерных признаков) и методологию оптимизации 3D алгоритма конечных разностей (3DFD), который используется для решения акустического волнового уравнения с константной или переменной плотностью изотропной среды (Iso3DFD). Начиная с простейшей реализации 3DFD, мы опишем методологию для оценки наилучшей производительности, которая может быть получена для данного алгоритма, с помощью его характеризации на конкретной вычислительной системе.
Введение
Метод конечных разностей во временной области – широко применяемая техника моделирования волн, например, для анализа волновых явлений и сейсморазведки. Этот метод популярен при использовании таких техник сейсмического анализа, как обратная временная миграция (reverse time migration) и полноволновая инверсия (full waveform inversion). Разновидности метода включают рассмотрение волн как акустических или упругих, а среда распространения может являться анизотропной, при этом плотность может также варьироваться.
Как известно, выбор конкретной численной схемы для аппроксимации частных производных имеет сильное влияние на производительность реализации [1]. В частности, это влияет на арифметическую интенсивность (число операций с плавающей запятой на каждое пересланное машинное слово) 3DFD алгоритма. Данная арифметическая интенсивность может быть далее связана с ожидаемой производительностью, используя методологию roofline моделирования [2]. Эта методология позволяет оценить уровень производительности реализации относительно максимально достижимой на конкретной вычислительной системе. То есть, roofline модель устанавливает рамки роста производительности, которая может быть достигнута с помощью оптимизации исходного кода программы. После того, как производительность реализации достигла определенного уровня, дальнейший рост производительности может быть получен только с помощью изменения самого алгоритма.
Для любого данного компьютера, его спецификация определяет пиковые значения для количества операций с плавающей запятой (FLOP/s) и для пересылок данных из памяти или в память (пропускная способность памяти). Соответствующие максимально достижимые показатели могут быть получены путем запуска стандартных бенчмарков как LINPACK [3] и STREAM triad [4].
Первая часть статьи будет нацелена на оценку максимально достижимой производительности ядра алгоритма Iso3DFD на двухсокетном сервере и сопроцессоре. Далее мы опишем несколько техник которые могут иметь важное влияние на производительность. Как обычно, такие оптимизации могут потребовать некоторых усилий и модификации исходного кода. После этого мы покажем вспомогательное средство для нахождения, если не наилучшего, то в какой-то степени оптимального набора параметров для компиляции и запуска приложения.
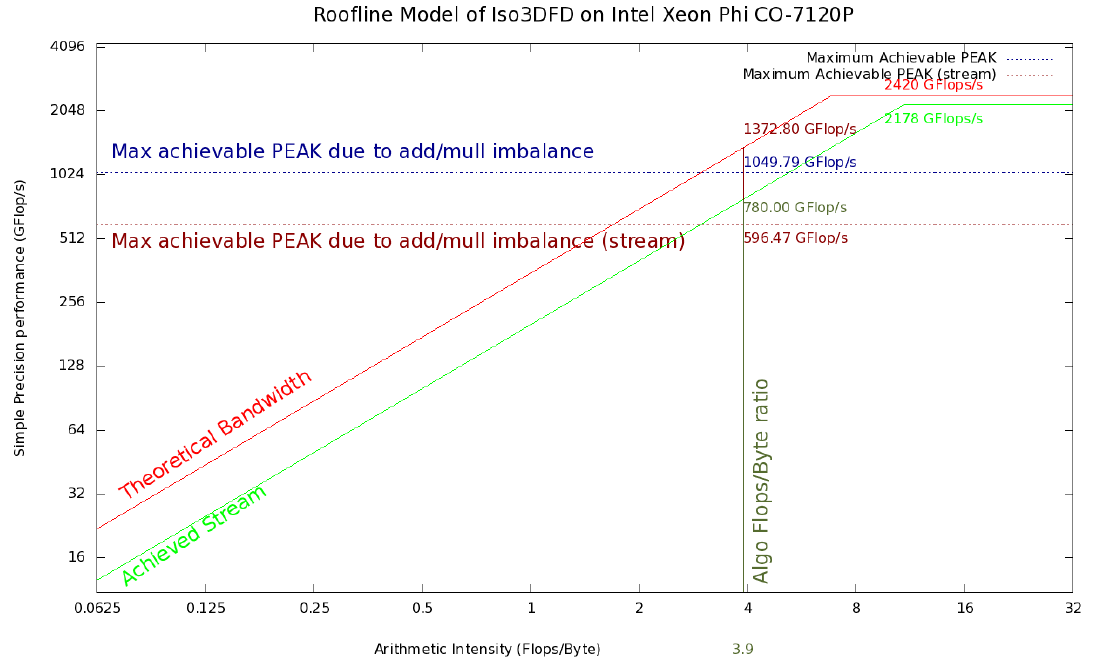
Рисунок 2. Roofline модель Iso3DFD для сопроцессора Xeon Phi 7120P. Красная и светло-зеленые линии обозначают верхний теоретический и достижимый предел на текущей платформе соответственно. Горизонтальная синяя линия отражает максимально достижимые значения пропускной способности памяти, принимая во внимание определенный дисбаланс сложений и умножений (#ADD;#MUL) и усредненные с помощью Stream triad бенчмарка (горизонтальная коричневая линия). Вертикальная темно-зеленая линия соответствует арифметической интенсивности для ядра Iso3DFD алгоритма. Пересечения с остальными линиями дают соответствующие достижимые пределы.
Оценка производительности
Наше ядро алгоритма Iso3DFD решает акустическое изотропное волновое уравнение 16 порядка дискретизации по пространству и 2 порядка дискретизации по времени. Стандартная реализация данного 3DFD ядра обычно достигает менее чем 10% от пиковой производительности вычислительной системы на операциях с плавающей запятой в секунду (FLOP/s). Мы рассмотрим способ получения roofline модели [2] для вычислительного ядра Iso3DFD на CPU и сопроцессоре Xeon Phi. Для нахождения максимальной производительности данного приложения нам необходимо найти:
- Пиковое значение производительности и пропускной способности памяти (теоретические): 2420 GFLOP/s в одинарной точности и 352 GB/s для Intel Xeon Phi 7120A; 1036 GFLOP/s в одинарной точности и 119 GB/s для 2 процессоров Intel Xeon E5-2697v2 с 1866 MHz DDR3 памятью.
- Значения полученные на Linpack (или GEMM) and STREAM triad бенчмарках дают нам соответствующие показатели максимальной производительности на платформе: 2178 GFLOP/s и 200 GB/s для Intel Xeon Phi 7120A; 930 GFLOP/s и 100 GB/s для 2 процессоров Intel Xeon E5-2697v2 с 1866 MHz DDR3 памятью.
- Арифметическая интенсивность приложения рассчитывается на базе количества сложений и умножений (ADD, MUL) чисел с плавающей запятой и количества байт пересланных из памяти и определенной количеством загрузок и записей в память (LOAD, STORE).
Последний пункт следует из предположения, что вычислительная система имеет кэш с бесконечной пропускной способностью памяти и размером, а также имеет нулевую задержку на доступ к данным (latency). Это определяет своего рода безупречную подсистему памяти, где любой массив загружается полностью даже в том случае, если требуется всего 1 элемент.
Несколько других факторов также могут влиять на производительность всего приложения, использующая 3DFD ядро – выбор граничных условий, IO схема при обращении во времени, а также технология или модель параллельного программирования. Однако, в приведенном здесь анализе мы не рассматриваем граничные условия и IO. Параллельная реализация решения данной задачи использует метод domain decomposition для распределенных систем с использованием MPI стандарта вместе с параллелизмом по потокам на вычислительном узле с использованием OpenMP. В данной работе рассматривается вычисления в подобласти на одном узле вычислительной системы.
Арифметическая интенсивность платформы
Наша тестовая система состоит из двух CPU Xeon E5-2697 (2S-E5) с 12 ядрами на один CPU, каждый запущен с частотой 2.7 ГГц без турбо режима. Данные процессоры поддерживают AVX расширение набора инструкций с 256-битной шириной векторных регистров. Данные инструкции могут выполнять вычисления с 8 числами с плавающей запятой в одинарной точности (32 бита) одновременно (за один такт CPU). Таким образом, теоретическую пиковую производительность можно посчитать как 2.7 (GHz) x 8 (SP FP) x 2 (ADD/MULL) x 12 (cores) x 2 (CPUs) = 1036,8 GFLOP/s. Пиковая пропускная способность рассчитывается с помощью частоты памяти (1866 ГГц), количества каналов памяти [4], количества байт пересылаемых в один такт (8), что дает 1866 x 4 x 8 x 2(CPUs) = 119 GB/s для двухпроцессорного узла 2S-E5. Также, нам необходимо оценить реально достижимые значения пропускной способности и производительности для характеризации поведения приложения. В качестве первого приближения допустим, что производительность любого реального приложения может быть ограничена пропускной способностью памяти (totally bandwidth bound), что в данной работе оценивается с помощью Stream triad или быстродействием процессора (totally FLOP/s bound или compute bound или CPU bound), что показывает бенчмарк Linpack. Выбор именно этих двух бенчмарков является чисто гипотетическим, но мы можем утверждать, что если они и далеки от идеальных оценок, то уж точно они лучше подходят в качестве приближения, чем пиковые теоретические значения вычислительной системы.
На 2S-E5 системе Linpack дает 930 GFLOP/s, а Stream triad 100 GB/s. Далее мы можем посчитать арифметическую интенсивность (AI) для теоретических и реальных максимальных показателей соответственно, как:
AI (theoretical, CPU) = 1036,8 / 119 = 8,7 FLOP/byte
AI (achievable, CPU) = 930 / 100 = 9,3 FLOP/byte
С данными значениями мы можем характеризовать любое вычислительное ядро следующим образом: если арифметическая интенсивность ядра больше (меньше) чем 9,3 FLOP/byte мы можем сказать, что это ядро ограничено быстродействием процессора — CPU bound (пропускной способностью памяти – memory bound).
Аналогичные расчеты на Linpack и Stream triad для Xeon Phi дают 2178 GFLOP/s и 200 GB/s соответственно. Теоретические пиковые оценки — 2420 GFLOP/s и 352 GB/s. Таким образом, арифметическая интенсивность будет равна:
AI (theoretical, Phi) = 2420,5 / 352 = 6,87 FLOP/byte
AI (achievable, Phi) = 2178 / 200 = 10,89 FLOP/byte
Арифметическая интенсивность вычислительного ядра
Roofline модель также требует вычисления арифметической интенсивности данного приложения. Она может быть получена через подсчет количества арифметических операций и доступов в память путем визуальной инспекции кода или с помощью специальных средств имеющих доступ к счетчикам вычислительной системы. В рамках стандартного вычислительного ядра схемы конечных разностей [5] мы можем найти 4 загрузки (coeff, prev, next, vel), 1 запись (next), 51 сложение (вычисления индексов не берутся в расчет) и 27 умножений (рисунок 3).
for(int bz=HALF_LENGTH; bz<n3; bz+=n3_Tblock)
for(int by=HALF_LENGTH; by<n2; by+=n2_Tblock)
for(int bx=HALF_LENGTH; bx<n1; bx+=n1_Tblock) {
int izEnd = MIN(bz+n3_Tblock, n3);
int iyEnd = MIN(by+n2_Tblock, n2);
int ixEnd = MIN(n1_Tblock, n1-bx);
int ix;
for(int iz=bz; iz<izEnd; iz++) {
for(int iy=by; iy<iyEnd; iy++) {
float* next = ptr_next_base + iz*n1n2 + iy*n1 + bx;
float* prev = ptr_prev_base + iz*n1n2 + iy*n1 + bx;
float* vel = ptr_vel_base + iz*n1n2 + iy*n1 + bx;
for(int ix=0; ix<ixEnd; ix++) {
float value = 0.0;
value += prev[ix]*coeff[0];
for(int ir=1; ir<=HALF_LENGTH; ir++) {
value += coeff[ir] * (prev[ix + ir] + prev[ix - ir])
;
value += coeff[ir] * (prev[ix + ir*n1] + prev[ix -
ir*n1]);
value += coeff[ir] * (prev[ix + ir*n1n2] + prev[ix -
ir*n1n2]);
}
next[ix] = 2.0f* prev[ix] - next[ix] + value*vel[ix];
}
}}}
Рисунок 3. Исходный код вычислительного ядра с cache blocking
Арифметическая интенсивность может быть рассчитана по формуле:
AI = (#ADD + #MUL) / ((#LOAD + #STORE) x word size) (1)
Это дает арифметическую интенсивность, равную 3,9 FLOP/byte, которую мы умножим на теоретическую пропускную способность каждой платформы для получения первой оценки максимально достижимой производительности для данного алгоритма. Получим 1372,8 GFLOP/s на Xeon Phi и 461,1 GFLOP/s на 2S-E5. Однако теоретическое пиковое значение производительности предполагает параллельное использование двух конвейеров (один для ADD, другой для MUL), что невозможно в данном вычислительном ядре из-за дисбаланса между сложениями и умножениями, таким образом, данный код не сможем достичь этого оцененного максимального значения. А это значит, что достижимое максимальное значение следует усреднить с помощью:
(#ADD + #MUL) / (2 x max(add, mul)), (2)
что отражает отношение общего возможного количества операций при 16 операциях с плавающей запятой на такт (ops/cycle) и максимально количества сложений и умножений, которые исполняются при 8 ops/cycle, предполагая использование одной 256-битной AVX SIMD вычислительной единицы. Это даст теоретическую оценку пиковой производительности, учитывающую дисбаланс сложений и умножений.
Рисунки 1 и 2 показывают Roofline модель с верхними границами в 354,9 GFLOP/s и 1049,8 GFLOP/s для 2S-E5 и Xeon Phi соответственно, полученных с помощью этой усредненной версией арифметической интенсивности.
Более реалистичная roofline модель может быть получена при использовании пропускной способности Stream triad бенчамарка умноженной на арифметическую интенсивность вычислительного ядра (390 GFLOP/s и 780 GFLOP/s соответственно). Еще более реалистичную модель можно получить, если учесть некоторый дисбаланс сложений и умножений (с помощью (2)), что показано красной пунктирной линией. Новая верхняя граница будет равна около 298 GFLOP/s для 2S-E5 и 596 GFLOP/s для Xeon Phi. Так как наша модель основана на безупречной модели кэш-памяти, мы предполагаем, что получившиеся значения все еще являются грубой оценкой максимально достижимых значений производительности. Как продемонстрировано в [2], можно улучшить получившийся roofline добавлением некоторых новых сущностей в характеризацию вычислительной системы, как, например, влияние и ограничения кэш памяти.
Продолжение следует…
Список литературы
- D. Imbert, K. Immadouedine, P. Thierry, H. Chauris, and L. Borges, “Tips and tricks for finite difference and i/o-less fwi,” in Expanded Abstracts. Soc. Expl. Geophys., 2011, pp. 3174–3178.
- S. Williams, A. Waterman, and D. Patterson, “Roofline: an insightful visual performance model for multicore architectures,” Communications of the ACM — A Direct Path to Dependable Software, vol. 52, pp. 65–76, April 2009.
- J. Dongarra, P. Luszczek, and A. Petitet, “The linpack benchmark: past, present and future,” Concurrency and Computation: Practice and Experience, vol. 15, no. 9, pp. 803–820, 2003, doi:10.1002/cpe.728.
- J. D. McCalpin, “Stream: Sustainable memory bandwidth in high performance computers,” University of Virginia, Charlottesville, Virginia, Tech. Rep., 1991-2007, a continually updated technical report. www.cs.virginia.edu/stream
- L. Borges, “Experiences in developing seismic imaging code for Intel Xeon Phi coprocessor.”, 2012. software.intel.com/en-us/blogs/2012/10/26/experiences-in-developing-seismic-imaging-code-for-intel-xeon-phi-coprocessor
- J. H. Holland, “Genetic algorithms and the optimal allocation of trials,” SIAM Journal of Computing, vol. 2, no. 2, pp. 88–105, 1973.