Comments 100
Лучше Jump Point
Не знаю на сколько быстрого, но есть алгоритм, когда придерживаешься всегда одной стенки лабиринта. Например, правой.
Т.е:
если справа есть стенка, то идем прямо,
если справа стенка и впереди стенка, то поворачиваем налево,
если справа нет стенки, то поворачиваем направо.
Т.е:
если справа есть стенка, то идем прямо,
если справа стенка и впереди стенка, то поворачиваем налево,
если справа нет стенки, то поворачиваем направо.
Ну да, правило одной руки всегда было вполне себе рабочим алгоритмом прохождения лабиринтов, насколько я помню.
Алгоритмы «одной руки» и А* рабочие, но не быстрые (по отношению к этому лабиринту). Поскольку все тупиковые узлы которые алгоритм проходит он проходит 2жды. И чем больше таких узлов будет тем дольше будет работать алгоритм.
Можно сделать такой лабиринт, в котором при использовании этого правила некоторые области будут недостижимы.
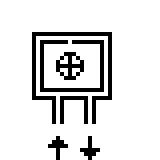 Попадите в центральную область.
Попадите в центральную область.Ок, выберитесь из центральной области следуя правилу одной руки, если вам от этого будет легче.
В топике рассматривается несколько иной лабиринт. По этому вариант с правилом одной руки для него вполне подходит.
К тому же мы находимся в начале лабиринта и не можем попасть в ситуацию когда зациклимся.
Вот на сколько быстро будет работать этот алгоритм не известно. Да и врятли он найдет больше 1 пути выхода.
К тому же мы находимся в начале лабиринта и не можем попасть в ситуацию когда зациклимся.
Вот на сколько быстро будет работать этот алгоритм не известно. Да и врятли он найдет больше 1 пути выхода.
Я не специалист, но мне кажется что с использованием такого алгоритма будет достигнута цель — выход из лабиринта. Если притом ставить цель найти какой-то спрятанный предмет, да еще чуть ли не в изолированной области, то это уже задача для другого алгоритма.
Если вы уже находитесь в этой недостижимой области, то выход для вас будет так же недостижим. Выберитесь из центральной области лабиринта на картинке выше.
А как я туда попаду по такому алгоритму?
Что значит «как попадёте»? Если вы уже не в лабиринте, то и выходить из него не надо, никакие алгоритмы не нужны. Если вы уже в лабиринте, то вы можете быть в абсолютно любой точке. Если алгоритм не работает для любой точки из которой возможно попасть в искомую, это означает, что он не работает вообще.
Я всегда считал что есть вход и есть выход и надо попасть от одного к другому. Варианты, когда в бессознательном состоянии попадаю в недостижимую область как-то не рассматривались. С утверждением про то, что алгоритм не работает в общем случае согласен, но от входа до выхода он проведет.
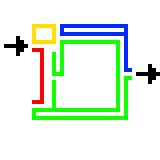 Попадите из входа, отмеченного стрелочкой к выходу, отмеченному стрелочкой, следуя правилу одной руки.
Попадите из входа, отмеченного стрелочкой к выходу, отмеченному стрелочкой, следуя правилу одной руки.Да легко. Проходим от выхода «нарисованного стрелочкой» до, скажем, выхода между красным и зелёным кусками, переходим на другую стену и снова применяем «правило правой руки». Грубо говоря просто считаем, что все остальные выходы забаррикадированы и применяем после этого «правило правой руки».
Я не могу понять: то ли вы не понимаете как работает (и гарантированно работает! — при определённых ограничениях) «правило правой руки», то ли просто троллите, честное слово.
Я не могу понять: то ли вы не понимаете как работает (и гарантированно работает! — при определённых ограничениях) «правило правой руки», то ли просто троллите, честное слово.
при определённых ограничениях
При очень строгих ограничениях. Для приведенных выше лабиринтов, оно нифига не работает.
Оно работает для любых лабиринтов при условии что мы начинаем и заканчиваем на краю. Приведённый в статье лабиринт (да и вообще большинство лабиринтов, встрчающихся в разных журналах) сюда отличненько попадают.
P.S. А вообще грустно видеть, что Хабр превратился в ресурс где уже и математические истины минусуют. Скоро прогресс дойдёт до американского уровня и будем законодательно устанавливать чему равно Pi?
P.S. А вообще грустно видеть, что Хабр превратился в ресурс где уже и математические истины минусуют. Скоро прогресс дойдёт до американского уровня и будем законодательно устанавливать чему равно Pi?
Для любых лабиринтов, у которых вход и выход на краю, и выход всего один, или нас не интересует через какой выход выйти.
Оно работает для любых лабиринтов при условии что мы начинаем и заканчиваем на краю.
а также при условии, что край у этого лабиринта один, что лабиринт нарисован на плоскости, что он не меняется во времени, что в нём нет порталов и полупроводящих стенок… Начиная с некоторого момента эти ограничения кажутся «очень строгими».
Это всё по большей части «нереальные» условия, которые в основ реализуются только в виртуальных лабиринтах (виртуальные миры, фильм «Начало» и т.п.). В реальной жизни я не видел порталов, несколько краев (это как вообще), по времени тоже редко меняются лабиринты. А неплоский или имеющий полупроводящие стенки лабиринт тоже довольно экзотичен для реального мира.
Но зато у алгоритма «правой руки» есть большой бонус в том, что он почти не использует дополнительную память. Я бы посмотрел на человека, который проходит сложный лабиринт волновым или другими сложным обходом, где надо запоминать O(длина пройденного пути) информации. А вот с обходом «правой руки» всё заметно проще.
Но зато у алгоритма «правой руки» есть большой бонус в том, что он почти не использует дополнительную память. Я бы посмотрел на человека, который проходит сложный лабиринт волновым или другими сложным обходом, где надо запоминать O(длина пройденного пути) информации. А вот с обходом «правой руки» всё заметно проще.
Ситуация «пройти к беседке в центре лабиринта» довольно реальна. Всякие проходы на разных уровнях и мостики тоже не требуют виртуальной реальности — они замечательно реализуются и в физической Вселенной. И запросто превращают «правило правой руки» в алгоритм «как с наибольшими затратами вернуться обратно ко входу»
А неплоский… лабиринт тоже довольно экзотичен для реального мира.

Роль порталов в реальном мире играют какие-нибудь лифты, поезда в аэропортах, метро… В общем, средства, позволяющие попасть в точку, недостижимую (или труднодостижимую) ногами. Лабиринт с несколькими краями — например, лабиринт, построенный вокруг озера. У него есть внешний и внутренний край. С лабиринтом, меняющимся во времени, я сталкиваюсь каждый день: по вечерам охранник закрывает калитку, проход через которую значительно сокращает путь до метро. В результате то, что было проходом, превращается в два тупика. Полупроводящие стенки можно найти в каждом аэропорту: когда, выйдя на улицу, обнаруживаешь, что чтобы попасть обратно, приходится идти довольно далеко, да ещё и стоять в очереди на просвечивание. Ну, и вообще, двери, открывающиеся только с одной стороны, в нашем мире не редкость. Так что ничего виртуального для реализации не требуется, всё уже придумано и воплощено.
вот машинка, выезжающая из лабиринта по такому алгоритму: marsohod.org/index.php/projects/plata1/29-labirint
Правило одной руки, кстати, работает только если вы входите в лабиринт снаружи. А если вы «проснулись» внутри лабиринта, то вы вполне можете оказаться на «острове». Для того, чтобы выбраться из такой ситуации, необходимо запоминать, где вы идете и в случае хождения по кругу совершать «левый» поворот. Ну а дальше уже вопрос с перепрыгиванием с одного острова на другой встаёт…
Такой алгоритм очень неприятно циклится вокруг столба, да и не уверен что он с ходу даст ответ, если выхода не существует
Было-бы интересно услышать, какие еще алгоритмы можно применить, для быстрого поиска пути в большом лабиринте?
A*, можно в сторону Jump Point Search посмотреть еще: Алгоритм поиска пути Jump Point Search
Самый дубовый алгоритм — залить краской в пейнте.
И что получите? :) Просто разукрасите все связанные пути в один цвет.
Заливать можно не только проходы, но и стенки. Комбинируя, можно даже в самых тяжёлых случаях по крайней мере выделить области, где перебирать дальше.
Я не совсем понял Вашу мысль. Если просто взять и залить в пейнте краской от входа, то весь лабиринт из белого станет другого цвета.
Вот как оно выглядит на этом лабиринте, если залить правую стенку: i39.tinypic.com/118qgp5.png
Кстати, вариантов прохождения-то минимум два получается.
Кстати, вариантов прохождения-то минимум два получается.
То есть ровно два.
Конкретно в этом случае, да, ровно два прохода
Спасибо, теперь дошло.
Paint на Core i3 минуты полторы думал, пока искал пиксели, которые надо закрасить. Кстати, закрасил все кроме стенок, так-что полностью заблокированные части лабиринта отсутствуют.
Там выше пояснили, заливать нужно стенки.
Если более аккуратно реализовать волну, без рекурсии — проблемы не возникнет. Зато гарантированно найдет выход отовсюду.
Интересно стало узнать его прохождение и погуляв еще по сети, я так и не нашел, рабочей программной реализации, решения лабиринта.
Спасибо, поржал. Алгоритм для поиска кратчайшего маршрута называется алгоритм Дейкстры. Там же можно найти реализацию. Этот алгоритм отлично ложится на поиск в лабиринте, где выбираются единичные ребра при прохождении. Алгоритм крайне эффективный и находит кратчайший маршрут очень быстро.
Здесь имеется в виду прохождение конкретно этого лабиринта.
Дейкстра для такого лабиринта будет работать даже медленнее обхода в ширину. У обхода в шиниру сложность будет O(N^2), а у дейкстры с кучей O(N*N*logN), без кучи — O(N^4).
Вот здесь код:
Не могли бы вы указать, где тут куча и O(N^4)?
Реализация
'''
Created on 21.10.2013
@author: gridem
'''
import png
from copy import deepcopy
def toArray(filename):
_, _, lines, _ = png.Reader(filename=filename).asDirect()
return [[0 if pixel == 0 else 1 for pixel in line[::3]] for line in lines]
def fromArray(ar, filename):
def toPixel(v):
return {0: [0, 0, 0], 1: [0, 255, 0], 2: [255, 255, 255], 3: [255, 0, 0]}[v]
def flatten(l):
return [i for s in l for i in s]
im = [flatten([toPixel(v) for v in line]) for line in ar]
png.from_array(im, mode='RGB').save(filename)
def findPath(arSource):
ar = deepcopy(arSource)
beg = (0, 1)
end = (len(ar) - 2, len(ar[0]) - 1)
counter = [-1] # workaround
qu = []
def add(pnt):
qu.append((pnt, counter[0]))
def pop():
counter[0] += 1
return qu[counter[0]][0]
add(beg)
while True:
p = pop()
x, y = p
ar[x][y] = 2
if p == end:
break
def tryAdd((x, y), (dx, dy)):
if (ar[x+dx][y+dy] == 1):
add((x + dx, y + dy))
tryAdd(p, (0, 1))
tryAdd(p, (1, 0))
tryAdd(p, (0, -1))
tryAdd(p, (-1, 0))
cnt = counter[0]
while cnt >= 0:
(x, y), cnt = qu[cnt]
ar[x][y] = 3
return ar
ar1 = toArray('''input.png''')
ar2 = findPath(ar1)
fromArray(ar2, '''output.png''')
Не могли бы вы указать, где тут куча и O(N^4)?
Результат

В общем, да, говорил «Дейкстра», подразумевал поиск в ширину. В целом, реализация выше как раз и есть поиск в ширину.
Как вариант воспользоваться свойством тока — течет по самому короткому пути.
Вытравить плату по рисуку не тяжело. Но на сколько поню, квантовые ПК как раз так и решают задачи…
Вытравить плату по рисуку не тяжело. Но на сколько поню, квантовые ПК как раз так и решают задачи…
А не проще ли было использовать стандартный метод обхода в ширину?
При чем, не надо строить никакого графа, просто в очередь складываются пары координат клеток. Изначально там лежит только начальная клетка. Потом из очереди извлекаются координаты, в цикле просматриваются 4 соседние клетки, и если они еще не помечены, то помещаются в очередь. Для таких размеров работать будет в пределах пол секунды, проблем со стеком быть не может. Дополнительной памяти надо 1 массив 600*600 и 2 массива такого де размера, но линейных. Автоматически находится именно кратчайший путь.
Если интересует не именно кратчайший, а вообще любой путь, то обычный поиск в глубину (реализуется также рекурсивно, как у вас setBlankAsDeadblockRec реализованно, только запускается с начала и красит все белые клетки, от уже покрашенных клеток запускатся не надо.
При чем, не надо строить никакого графа, просто в очередь складываются пары координат клеток. Изначально там лежит только начальная клетка. Потом из очереди извлекаются координаты, в цикле просматриваются 4 соседние клетки, и если они еще не помечены, то помещаются в очередь. Для таких размеров работать будет в пределах пол секунды, проблем со стеком быть не может. Дополнительной памяти надо 1 массив 600*600 и 2 массива такого де размера, но линейных. Автоматически находится именно кратчайший путь.
Если интересует не именно кратчайший, а вообще любой путь, то обычный поиск в глубину (реализуется также рекурсивно, как у вас setBlankAsDeadblockRec реализованно, только запускается с начала и красит все белые клетки, от уже покрашенных клеток запускатся не надо.
Нафига нужен код:
когда начало в точке 1,1. Вместо этого стоило бы написать setBlankAsDeadblockRec(1,1);
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
когда начало в точке 1,1. Вместо этого стоило бы написать setBlankAsDeadblockRec(1,1);
Алгоритм такой:
Выполнять рекурсивную функцию по всем точкам дорог лабиринта:
1. Если мы стоим на дороге и вокруг нас 3 стены, помечаем место где мы стоим как тупик, в противном случае выходим из функции;
2. Переходим на место которое не является стенкой из пункта №1, и повторяем пункт №1;
Этот код необходим, для прохода всех точек, и обнаружения тупиковых.
Если такая найдена, запускается рекурсивная функция setBlankAsDeadblockRec(i,j) с координатами тупиковой позиции, и заполняется «дедблоками» до выхода из тупиковой дороги, продолжаем setDeadblock (перебор всех точек).
Ваше предложение приведет к выходу из функции.
Тупиковые точки будут и так найдены в ходе рекурсии. Скорее всего, ваш алгоритм работает только из-за совпадения, что цикл начинается в точке (1,1). Попробуйте изменить
for i:=1 to N-1 do на for i:=N-1 downto 1 do и посмотрите, что будет.Ничего не произойдет. Будет точно такой-же результат (я попробовал на всякий случай). Здесь перебор всего массива осуществлен только для того чтоб найти все тупиковые точки, тоесть:
И еще, возможно это вас сбивает с толку, когда вызывается рекурсивная функция setBlankAsDeadblockRec(i,j), возвращение в цикл происходит только после выхода из нее.
if LABIRINT[x,y]=blank then //...Если мы стоим на дороге... begin if LABIRINT[x-1,y]<>BLANK then k:=k+1; if LABIRINT[x,y-1]<>BLANK then k:=k+1; if LABIRINT[x+1,y]<>BLANK then k:=k+1; if LABIRINT[x,y+1]<>BLANK then k:=k+1; if k=4 then LABIRINT[x,y]:=DEADBLOCK; if k=3 then//...и вокруг нас 3 стены... begin LABIRINT[x,y]:=DEADBLOCK; //...помечаем место где мы стоим как тупик.. if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);//Переходим на место которое не является стенкой... if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);//-//- if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);//-//- if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);//-//- end; end;//...в противном случае выходим из функции...
И еще, возможно это вас сбивает с толку, когда вызывается рекурсивная функция setBlankAsDeadblockRec(i,j), возвращение в цикл происходит только после выхода из нее.
В том-то и дело, что если в лабиринте нет клеток полностью изолированных от остального лабиринта, то обычная рекурсия обойдет его целиком.
Делал когда-то: aivanov.com/maze-generator/
Делал когда-то: aivanov.com/maze-generator/
Согласен, но для прохода всего лабиринта обычной рекурсией, функцие придется при выходе на дорогу, которая окажется тупиковой, будет возвращаться, в таком случае, все тупиковые дороге будут пройдены 2 раза. Что снижает скорость работы алгоритма.
Представленная рекурсивная функция, завершает работать только в том случае, если «находимся на дороге, а вокруг все стены» и «если находимся на дороге, а вокруг 1 стена и 2 дороги». И не проходит по одним и тем-же дорогам.
Представленная рекурсивная функция, завершает работать только в том случае, если «находимся на дороге, а вокруг все стены» и «если находимся на дороге, а вокруг 1 стена и 2 дороги». И не проходит по одним и тем-же дорогам.
В обычной рекурсии функция setBlankAsDeadblockRec будет вызываться N*M раз, а у вас 2*N*M
Я с вами не согласен, покажите пожалуйста место в коде, где функция setBlankAsDeadblockRec будет вызываться 2*N*M раз.
LOL. Смотри мой первый комментарий в этом треде
Скажите мне, какой из варинтов будет запускаться N*M раз, а какой 2*N*M, и какая разница в них:
Вариант №1:
Вариант №2:
Вариант №1:
...
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[x+1,y]<>BLANK then inc(k);
if LABIRINT[x,y+1]<>BLANK then inc(k);
if LABIRINT[x-1,y]<>BLANK then inc(k);
if LABIRINT[x,y-1]<>BLANK then inc(k);
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y)
else if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1)
else if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y)
else if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
end;
end;
...
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
if LABIRINT[i,j]=blank then setBlankAsDeadblockRec(i,j);
end;
...
Вариант №2:
...
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[i,j]=blank then
begin
if LABIRINT[x+1,y]<>BLANK then inc(k);
if LABIRINT[x,y+1]<>BLANK then inc(k);
if LABIRINT[x-1,y]<>BLANK then inc(k);
if LABIRINT[x,y-1]<>BLANK then inc(k);
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y)
else if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1)
else if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y)
else if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
end;
end;
end;
...
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
...
Когда то тоже игрался с изображениями в Delphi.
bit.Canvas.Pixels[j,i] очень медленно работает.
Лучше используйте bit.ScanLine[i]
bit.Canvas.Pixels[j,i] очень медленно работает.
Лучше используйте bit.ScanLine[i]
Даешь соревнование программеров по реализации самого быстрого поиска решения? самого точного? Например, в виде веб страницы куда аплоадится такая двуцветная карта и на выходе получается картинка. :)
P.S. У A* скорость существенно зависит от эвристической функции. Можно попробовать подобрать наиболее удачную функцию именно для этой задачи — она не обязательно должна быть точной (эвклидово расстояние), ей достаточно быть сбалансированно «жадной», т.е. предпочитать движение в направлении выхода, но без отбрасывания развилок в противоположном направлении.
P.S. У A* скорость существенно зависит от эвристической функции. Можно попробовать подобрать наиболее удачную функцию именно для этой задачи — она не обязательно должна быть точной (эвклидово расстояние), ей достаточно быть сбалансированно «жадной», т.е. предпочитать движение в направлении выхода, но без отбрасывания развилок в противоположном направлении.
Например если движемся векторно правильно к выходу 10 очков, прямо 5 очков, поворот по правилу «одной руки» 3 очка? :D
Без шуток, примерно так и работает эвристическая функция в A*. Для каждой пройденной точки ставится некое количество очков (весовой коэффициент этого узла графа) и алгоритм стремится продолжать движение из самых «дорогих» точек. Мое первое (несколько дилетантское) знакомство с эвристикой пару лет назад: blog.runserver.net/2010/12/blog-post.html
А можно посмотреть на ваш поиск в ширину? Что-то мне подсказывает, что вы неправильно его реализовали и вместо фикса начали изобретать неоптимальный велосипед. При правильной реализации bfs на карте 600x600 найдет ответ почти мгновенно.
Можно попробовать алгоритм Ли (A* с 4мя направлениями) с функцией-предсказателем оценки стоимости раскрытия ячейки и поиском в глубину (когда раскрывается последняя ячейка из фронта поиска, если фронт не содержит ячеек с предсказанной стоимостью меньше, чем стоимость раскрытия ячейки по направлению следования фронта). Производительность сильно зависит от реализации фронта и поиска следующей ячейки для раскрытия из фронта.
Алгоритмы поиска пути хорошо изученная и давно избитая тема. Гораздо интереснее придумать, как генерировать лабиринты, которые кажутся сложными человеку.
А почему агоритм волновой выдает stack overflow?
Ответил ниже.
По той причине, что я подошел не правильно к применению алгоритма к данному лабиринту. А именно, без изменения рисунка. Волновой алгоритм применялся к лабиринту 1802*1802, с дорогой, толщиной в 4 пикселя, а прохождение производилось по-пиксельно.
Не судите строго люди. Я тут быстро набросал код(на Python), который использует циклическую очередь. Код написан не самым оптимальным способом, но он работает.
Вот пример по времени выполнения моей программы:
Вот пример по времени выполнения моей программы:
Prepare data: 0:00:00.306268
Finish queue: 0:00:01.727277
Finish update image: 0:00:03.976633
Save image: 0:00:04.123483
from datetime import datetime
from PIL import Image, ImageDraw
class Queue:
def __init__(self, size):
self._queue = range(size)
self._size = size
self._left = 0
self._right = 0
def push(self, element):
self._queue[self._right] = element
self._right += 1
if self._right + 1 == self._left:
raise Exception('Small queue')
if self._right >= self._size:
self._right = 0
def pop(self):
element = self._queue[self._left]
self._left += 1
if self._left >= self._size:
self._left = 0
return element
def run(self, func_next_step):
while self._left != self._right:
elements = func_next_step(self.pop())
for element in elements:
self.push(element)
if __name__ == '__main__':
start = datetime.now()
image = Image.open('source.png')
draw = ImageDraw.Draw(image)
pix = image.load()
width = image.size[0]
height = image.size[1]
pixel = []
for y in xrange(height):
line = []
for x in xrange(width):
line.append(pix[x, y][0])
pixel.append(line)
move = (
(0, 1, ),
(1, 0, ),
(0, -1, ),
(-1, 0, ),
)
def recovery_path(item):
element = item
while element is not None:
x = element[0]
y = element[1]
if pixel[x][y] == 3:
break
pixel[x][y] = 3
element = element[2]
def next_step(item):
step = []
for vector in move:
x = item[0] + vector[0]
y = item[1] + vector[1]
if 0 <= x < width and 0 <= y < height:
if pixel[x][y] == 255:
pixel[x][y] = 1
step.append((x, y, item))
elif item[2] is not None:
recovery_path(item)
return step
pixel[0][1] = 3
queue = Queue(200)
queue.push((1, 0, None))
print "Prepare data : %s" % (datetime.now() - start)
queue.run(next_step)
print "Finish queue : %s" % (datetime.now() - start)
for y in xrange(height):
line = pixel[y]
for x in xrange(width):
type = line[x]
color = pix[x, y][0]
if type == 1:
draw.point((x, y), (128, 128, 128))
elif type == 2:
draw.point((x, y), (0, 255, 255))
elif type == 3:
draw.point((x, y), (0, 255, 0))
elif type == 0:
draw.point((x, y), (0, 0, 0))
else:
draw.point((x, y), (255, 0, 0))
if color == 0 and type != 0:
draw.point((x, y), (255, 0, 0))
print "Finish update image : %s" % (datetime.now() - start)
image.save('answer.png')
print "Save image : %s" % (datetime.now() - start)
Алгоритм приведенный в статье работает 0,00761 секунды. Это без сканирования и построения изображения.
Без понятия как называется мой велосипед, т.к. плохо разбираюсь в алгоритмах, но используя очередь из «развилок» получил довольно простой код без рекурсии. Работает почти в 3 раза быстрее чем оригинал из статьи (у меня, примерно 0,0023 с)
Если отрисовать точки очереди получатся
procedure setPath;
var k,g:integer;
XX,YY:array [1..100000] of Integer;
begin
g:=0;
x:=1; y:=1; // начало пути
while ((x<>599) or (y<>599)) do // конец пути
begin
LABIRINT[x,y]:=DEADBLOCK;
k:=0;
if LABIRINT[x-1,y]=BLANK then k:=k+1;
if LABIRINT[x,y-1]=BLANK then k:=k+1;
if LABIRINT[x+1,y]=BLANK then k:=k+1;
if LABIRINT[x,y+1]=BLANK then k:=k+1;
if k>1 then
begin
g:=g+1;
XX[g]:=x;
YY[g]:=y;
end;
if k>=1 then
if LABIRINT[x-1,y]=BLANK then x:=x-1
else
if LABIRINT[x,y-1]=BLANK then y:=y-1
else
if LABIRINT[x+1,y]=BLANK then x:=x+1
else
if LABIRINT[x,y+1]=BLANK then y:=y+1;
if k=0 then
begin
if (x=XX[g]) and (y=YY[g]) then g:=g-1;
x:=XX[g];
y:=YY[g];
end;
end;
end;
Если отрисовать точки очереди получатся
наметки пути

По ошибке не учел привилегированное направление.
Конечно же гораздо эффективнее поменять порядок строк:
на
И получим еще пятикратный выигрыш по скорости. Полный цикл 0,000484 с.
Картина конечно станет
Конечно же гораздо эффективнее поменять порядок строк:
if LABIRINT[x-1,y]=BLANK then x:=x-1
else if LABIRINT[x,y-1]=BLANK then y:=y-1
else if LABIRINT[x+1,y]=BLANK then x:=x+1
else if LABIRINT[x,y+1]=BLANK then y:=y+1;
на
if LABIRINT[x+1,y]=BLANK then x:=x+1
else if LABIRINT[x,y+1]=BLANK then y:=y+1
else if LABIRINT[x-1,y]=BLANK then x:=x-1
else if LABIRINT[x,y-1]=BLANK then y:=y-1;
И получим еще пятикратный выигрыш по скорости. Полный цикл 0,000484 с.
Картина конечно станет
более адекватной

Действительно, после изменения порядка проверки, скорость алгоритма выросла. Изменяем код в
И имеем скорость работы: 0,000431 секунды. Боюсь, что есть смысл замерять скорость работы, на одном железе, и то меняется после каждого перезапуска, в зависимости от состояния ОС.
procedure setBlankAsDeadblockRec(x,y:integer);
...
///смотрим ниже
...
И имеем скорость работы: 0,000431 секунды. Боюсь, что есть смысл замерять скорость работы, на одном железе, и то меняется после каждого перезапуска, в зависимости от состояния ОС.
Прошу прощения, неудачно вставил код, и не успевал отредактировать.
Вот он:
Вот он:
...
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);
if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);
if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);
if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
end;
...
Т.е. ваш код тоже заработал быстрее? Это странно, т.к. выигрыш ведь происходил за счет разного подхода — ваш код ищет все возможные пути, а мой — любой из возможных (не обязательно оптимальный).
Поэтому в вашем варианте от изменения порядка строк, (по крайней мере у меня) скорость почти не изменилась. (я замеряю время 1000 циклов, и режим процессора меняю на realtime).
Визуально это видно по картинке. Ваш алгоритм просчитывает все поле, а мой — только серые области.

Кстати, поиск всех путей можно реализовать и с моим подходом. Нужно просто не останавливаться при достижении выхода, а продолжать расчет дальше. Если при этом помнить длину пути, то можно отсеивать неоптимальные варианты (если текущая длина пути + сумма расстояний до выхода по x и y, больше чем наименьший из найденных путей — то путь можно дальше не проверять).
По идее за счет отсеивания «лишних» путей, получим более быстрый поиск кратчайшего, чем, к примеру, поиск в ширину.
Поэтому в вашем варианте от изменения порядка строк, (по крайней мере у меня) скорость почти не изменилась. (я замеряю время 1000 циклов, и режим процессора меняю на realtime).
Визуально это видно по картинке. Ваш алгоритм просчитывает все поле, а мой — только серые области.

Кстати, поиск всех путей можно реализовать и с моим подходом. Нужно просто не останавливаться при достижении выхода, а продолжать расчет дальше. Если при этом помнить длину пути, то можно отсеивать неоптимальные варианты (если текущая длина пути + сумма расстояний до выхода по x и y, больше чем наименьший из найденных путей — то путь можно дальше не проверять).
По идее за счет отсеивания «лишних» путей, получим более быстрый поиск кратчайшего, чем, к примеру, поиск в ширину.
кажется не упоминали, но если в лабиринте много ветвлений или мы стоим в центре карты то волновой алгоритм расходится во все стороны, количество ячеек в волне увеличивается и соответственно увеличивается время просчета поэтому в таких случаях лучше использовать оптимизацию и пускать две волны — одну из начала лабиринта, другую из конца, поиск пути заканчивается когда волны соприкасаются, в некоторых случаях такая оптимизация дает очень значительный прирост производительности.
и погуляв еще по сети, я так и не нашел, рабочей программной реализации, решения лабиринта
Representing and solving a maze given an image
И опять-же, здесь говорится о конкретно етом лабиринте.
Sign up to leave a comment.
Алгоритм поиска путей в лабиринте