
Иллюстрация к последней задаче.
Существуют задачи с простыми и, казалось бы, очевидными решениями, которые, однако, трудно найти. При их решении опасно полагаться на интуицию, ведь правильный ответ зачастую совсем не совпадает с тем, который она подсказывает. В данной статье я предлагаю подборку из 10 таких заданий, упорядоченных по возрастанию сложности; их решения убраны под спойлер. Для получения верных ответов не нужно обладать какими-то специальными знаниями, достаточно лишь находчивости и знания школьной программы.
- Из городов A и B, расстояние между которыми 100 км, одновременно навстречу друг другу выезжают два поезда, их скорости 40 км/ч и 60 км/ч соответственно. Одновременно из города А в направлении B вылетает муха со скоростью 200 км/ч, летит до встречи с поездом, выехавшим из B, после чего летит к поезду, выехавшему из A, после этого снова летит к поезду, выехавшему из B, и т.д. Какое расстояние пролетит муха до того, как поезда встретятся?
РешениеСкорость сближения поездов 100 км/ч, расстояние между ними 100 км, значит, они встретятся через 1 час. Муха будет летать в течение этого часа со скоростью 200 км/ч и пролетит суммарно 200 км.
- В треугольнике ABC угол C прямой, BM — медиана. Доказать: ∠CAB > ∠ABM.
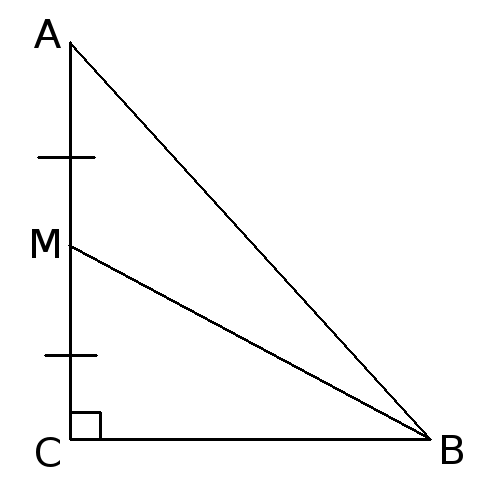
ДоказательствоВ треугольнике MBC катет CM меньше гипотенузы BM. MC=AM. Значит, MB > AM. Рассмотрим треугольник ABM, в нем сторона MB больше стороны AM. А напротив большей стороны лежит больший угол. Значит ∠CAB > ∠ABM. ЧТД.
- Граждане некой страны очень давно живут по следующим правилам: семья производит на свет детей до первого мальчика, после чего дети в семье не рождаются. Рождаются только мальчики и девочки с равными вероятностями; близнецы не рождаются. Определить долю мужского населения в этой стране. Считать, что смертность не зависит от пола.
РешениеЗадача-ловушка. Правило «в семье ровно один мальчик» никак не влияет на вероятность рождения мальчика в целом в стране. Правильный ответ: 50%.
- Две подружки одновременно начинают выполнять домашнюю работу, причём каждая из них решает семь задач в час с решебником, а без него — только четыре. Какая из девочек раньше освободится, если первая школьница отдала решебник подруге после того, как выполнила половину задания?
РешениеПоложим, что всего задание состоит из 28 задач. Половину задания (14 задач) первая решит с решебником за 14/7=2 часа, а вторая за это время решит 2*4=8 задач. Вооружившись решебником, вторая решит оставшиеся 28-8=20 задач за 20/7<3 часа, а первая за это время решит только 3*4=12 задач, а всего ей оставалось 14 задач. Следовательно, раньше с заданием справится вторая девочка.
- Железный лом лежит на куске льда, который плавает в бассейне. Как изменится уровень воды в бассейне, когда лед растает (а лом утонет)?
РешениеВспоминаем закон Архимеда: на тело, погружённое в жидкость, действует выталкивающая сила, равная силе тяжести вытесненной этим телом жидкости. Следует заметить, что тело должно быть полностью окружено жидкостью либо пересекаться с поверхностью жидкости. Так, например, закон Архимеда нельзя применить к лому, который лежит на дне бассейна. Таким образом, пока лед и лом плавают, масса лома и льда равна массе вытесненной воды. Когда лом опускается на дно, то объем вытесненной им воды равен объему лома. Масса льда равна массе воды, в которую он превратился, когда растаял, поэтому вклад льда можно не учитывать. (Кстати, по той же причине, если бы в исходной задаче не фигурировал лом, то ответ был бы, что уровень воды не изменится.) До таяния лом вытеснял больше воды, чем после таяния, так как вода имеет меньшую плотность, чем лом. Ответ: уровень воды в бассейне понизится. (Если предположить, что лёд и лом плавали в толще воды, а не на поверхности, то обоснование совсем упрощается: объем льда уменьшился, когда лёд растаял, а объем лома не изменился.)
- Число n — натуральное, число p — простое, доказать:
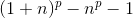 делится нацело на p. (Необходимо знание основ комбинаторики.)
делится нацело на p. (Необходимо знание основ комбинаторики.)
ДоказательствоВспомним бином Ньютона.
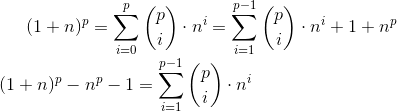
В последнем выражении каждый биномиальный коэффициент делится на p, так как p простое и находится в числителе в формуле биномиального коэффициента, а в знаменателе — произведение чисел, меньших p. ЧТД.
- Головоломка «Ханойские башни» состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из N дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3.

Решение
ejudge-проверка решения
- Сколько существует различных строк длины N, состоящих из символов «0» и/или «1», в которых две единицы не идут подряд? Ответом может служить рекуррентная формула.
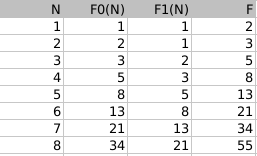
РешениеОбозначим F(N) число строк длины N, не содержащих две единицы подряд. Обозначим F0(N) число строк длины N, не содержащих две единицы подряд и заканчивающихся на 0. Обозначим F1(N) число строк длины N, не содержащих две единицы подряд и заканчивающихся на 1.
Выведем рекуррентные формулы для F0 и F1.
F1(N) = F0(N-1). Так как две единицы подряд идти не может, число строк, заканчивающихся на 1, равно числу строк на 1 меньшей длины, заканчивающихся на 0.
F0(N) = F0(N-1) + F1(N-1). Ноль можно дописать к любой корректной строке, не нарушив при этом условия. Значит, число строк, заканчивающихся на 0, равно числу строк на 1 меньшей длины.
F0(N) = F0(N-1) + F1(N-1) = F0(N-1) + F0(N-2). Итак, F0 представляет собой ряд Фибоначчи с неким сдвигом. F1(N) = F0(N-1), значит F1 тоже состоит из чисел Фибоначчи, с «отставанием» на 1 относительно F0.
F(N) = F0(N) + F1(N). Член F(N) получается, когда число из ряда Фибоначчи F0 складывают с числом из ряда Фибоначчи F1, которое является для него предыдущим числом. А сумма числа Фибоначчи с предыдущим числом Фибоначчи — это тоже число Фибоначчи (по формуле чисел Фибоначчи). Итак, мы доказали, что число строк, не включающих две единицы подряд, будет является числом Фибоначчи. Осталось определить значение F(N) для первых двух N. F(1) = 2 (две подходящие последовательности: «0» и «1»), F(2) = 3 (три подходящие последовательности: «00», «01», «10»).
- Акционеры сели за круглый стол, на котором были установлены таблички с их именами (на каждого акционера приходится одна табличка). Однако каждый сел за табличку с чужим именем. Доказать, что можно повернуть стол так, чтобы хотя бы 2 акционера сидели за своими табличками.
ДоказательствоКлючевым условием является факт, что вначале ни один акционер не сидит за своей табличкой. Пусть число акционеров равно N. Число состояний стола тоже N. На одном из состояний стола (начальном) ни один акционер не сидит за своей табличкой, следовательно состояний стола, при которых возможны сопоставления акционеров с табличками, равно N-1. Переберем эти N-1 состояний. За это время все N акционеров должны «побывать» за своими табличками. Согласно принципу Дирихле, хотя бы на одно из перебираемых N-1 состояний должно прийтись хотя бы два из N сопоставлений. Иными словами, найдется состояние, при котором хотя бы два акционера сидят за своими табличками. ЧТД.
- N мудрецов выстроились «паровозиком», на каждого надели колпак белого или черного цвета. Каждый мудрец слышит, что говорят вокруг, и видит цвета колпаков впереди стоящих мудрецов, но не видит свой колпак и колпаки мудрецов, стоящих сзади. Всем им по очереди, начиная с последнего, задается вопрос: «Какого цвета на тебе колпак?». Мудрецу разрешается отвечать только «белый» или «черный». Разработать алгоритм действий мудрецов такой, чтобы число правильных ответов было не меньше N-1.
РешениеОбозначим белый колпак единицей, черный колпак нулем. Последний мудрец складывает цвета колпаков впереди стоящих мудрецов по модулю 2 (ксорит их). Называет цвет, соответствующий получившейся сумме. Дальнейшая судьба последнего мудреца не так интересна: возможно, названный цвет совпал с цветом его колпака, возможно нет. Следующий мудрец, вычислив сумму колпаков впереди стоящих, складывает её с цветом, названным последним мудрецом, и получает цвет своего колпака, который и называет. Следующий за ним складывает уже три числа: число стоящих впереди белых колпаков и числа, сказанные двумя предыдущими мудрецами. Последующие мудрецы действуют по той же схеме. Получается не менее N-1 правильных ответов.

Прошу сообщать в комментариях об альтернативных способах выполнения заданий, в том числе более сложных или неудачных, а также о найденных ошибках и опечатках.
Приятного решения!
UPD. makaroni4 создал тест из некоторых задач. Спасибо!
Only registered users can participate in poll. Log in, please.
Сколько задач решили?
19.67% 8-10108
22.59% 5-7124
20.22% 3-4111
37.52% 0-2206
549 users voted. 519 users abstained.
Only registered users can participate in poll. Log in, please.
Интересные задачи
51.18% 1152
20.88% 262
46.8% 3139
29.63% 488
41.75% 5124
12.12% 636
20.88% 762
23.57% 870
39.73% 9118
53.2% 10158
297 users voted. 623 users abstained.