Привет, Habr.
НаGeektimes Habr было уже несколько статей про abc-гипотезу (например в 2013 и в 2018 годах). Сама история про теорему, которую сначала много лет не могут доказать, а потом столько же лет не могут проверить, безусловно заслуживает как минимум, художественного фильма. Но в тени этой чудесной истории, сама теорема рассматривается черезчур поверхностно, хотя она не менее интересна. Уже хотя бы тем, что abc-гипотеза — одна из немногих нерешенных проблем современной науки, постановку задачи которой сможет понять даже пятиклассник. Если же эта гипотеза действительно верна, то из нее легко следует доказательство других важных теорем, например доказательство теоремы Ферма.
Не претендуя на лавры Мотидзуки, ятоже решил попробовать решил проверить с помощью компьютера, насколько выполняются обещанные в гипотезе равенства. Собственно, почему бы нет — современные процессоры ведь не только для того чтобы в игры играть — почему бы не использовать компьютер по своему основному (compute — вычислять) предназначению…
Кому интересно что получилось, прошу под кат.
Начнем с начала. О чем собственно, теорема? Как гласит Википедия (формулировка в английской версии немного более понятна), для взаимно-простых (не имеющих общих делителей) чисел a, b и с, таких что a+b=c, для любого ε>0 существует ограниченное число троек a+b=c, таких что:
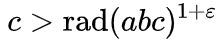
Функция rad называется радикалом, и обозначает произведение простых множителей числа. Например, rad(16) = rad(2*2*2*2) = 2, rad(17) = 17 (17 простое число), rad(18) = rad(2*3*3) = 2*3 = 6, rad(1000000) = rad(2^6 ⋅ 5^6) = 2*5 = 10.
Собственно, суть теоремы в том, что количество таких троек довольно мало. Например, если взять наугад ε=0.2 и равенство 100+27=127: rad(100) = rad(2*2*5*5) = 10, rad(27)=rad(3*3*3)=3, rad(127) = 127, rad(a*b*c) = rad(a)*rad(b)*rad(с) = 3810, 3810^1.2 явно больше 127, неравенство не выполняется. Но бывают и исключения, например для равенства 49 + 576 = 625 условие теоремы выполняется (желающие могут проверить самостоятельно).
Следующий ключевой для нас момент — этих равенств, согласно теореме, ограниченное число. Т.е. это значит, что их все можно просто попытаться перебрать на компьютере. В итоге, это дает намНобелевскую премию вполне интересную задачу по программированию.
Итак, приступим.
Первая версия была написана на Python, и хотя этот язык слишком медленный для подобных расчетов, писать код на нем легко и просто, что удобно для прототипирования.
Получение радикала: раскладываем число на простые множители, затем убираем повторы, преобразуя массив в множество. Затем просто получаем произведение всех элементов.
Взаимно-простые числа: раскладываем числа на множители, и просто проверяем пересечение множеств.
Проверка: используем уже созданные функции, тут все просто.
Желающие могут поэкспериментировать самостоятельно, скопировав вышеприведенный код в любой онлайн-редактор языка Python. Разумеется, код работает ожидаемо медленно, и перебор всех троек хотя бы до миллиона был бы слишком долгим. Ниже под спойлером есть оптимизированная версия, рекомендуется использовать ее.
Окончательная версия была переписана на С++ с использованием многопоточности и некоторой оптимизации (работать на Си с пересечением множеств было бы слишком хардкорно, хотя вероятно и быстрее). Исходный код под спойлером, его можно скомпилировать в бесплатном компиляторе g++, код работает под Windows, OSX и даже на Raspberry Pi.
Для тех кому лень устанавливать компилятор С++, приведена слегка оптимизированная Python-версия, запустить которую можно в любом онлайн редакторе (я использовал https://repl.it/languages/python).
Троек a,b,c действительно очень мало.
Некоторые результаты приведены ниже:
N=10: 1 «тройка», время выполнения <0.001c
1 + 8 = 9
N=100: 2 «тройки», время выполнения <0.001c
1 + 8 = 9
1 + 80 = 81
N=1000: 8 «троек», время выполнения <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N=10000: 23 «тройки», время выполнения 2с
N=100000: 53 «тройки», время выполнения 50c
При N=1000000 имеем всего лишь 102 «тройки», полный список приведен под спойлером.
Увы, программа работает все равно медленно, результатов для N=10000000 я так и не дождался, время вычисления составляет больше часа (возможно я где-то ошибся с оптимизацией алгоритма, и можно сделать лучше).
Еще интереснее посмотреть результаты графически:
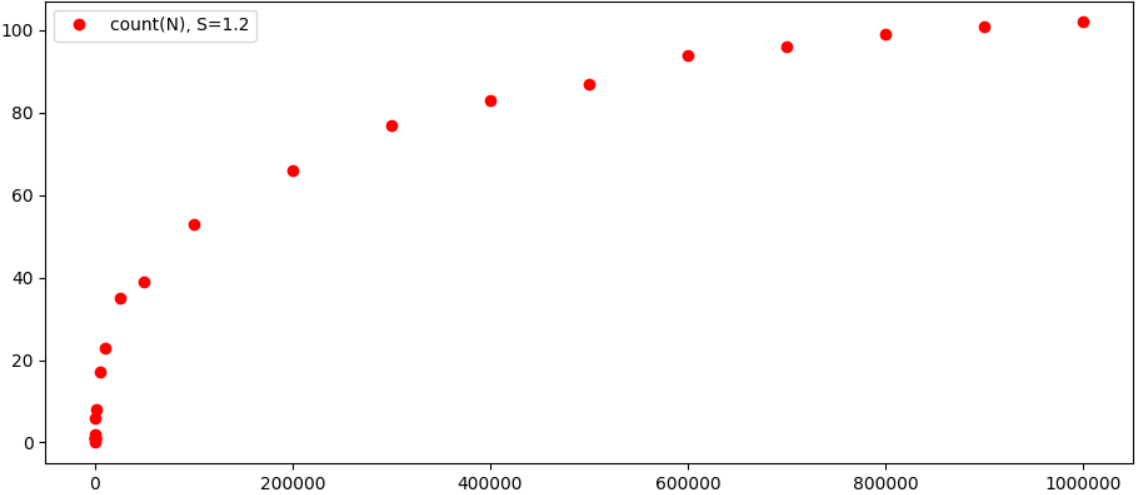
В принципе, вполне очевидно, что зависимость количества возможных троек от N растет заметно медленнее самого N, и вполне вероятно, что результат будет сходиться к какому-то конкретному числу для каждого ε. Кстати, при увеличении ε число «троек» заметно сокращается, например при ε=0.4 имеем всего 2 равенства при N<100000 (1 + 4374 = 4375 и 343 + 59049 = 59392). Так что в целом, похоже что теорема действительно выполняется (ну и наверное ее уже проверяли на компьютерах помощнее, и возможно, все это уже давно посчитано).
Желающие могут поэкспериментировать самостоятельно, если у кого будут результаты для чисел 10000000 и выше, я с удовольствием добавлю их к статье. Разумеется, было бы интересно «досчитать» до того момента, когда множество «троек» совсем перестанет расти, но это может занять реально долгое время, скорость расчета похоже зависит от N как N*N (а может и N^3), и процесс весьма долгий. Но тем не менее, удивительное рядом, и желающие вполне могут присоединиться к поиску.
Правка: как подсказали в комментариях, в Википедии таблица с результатами уже есть — в диапазоне N до 10^18 количество «троек» все же растет, так что «конец» множества пока не найден. Тем интереснее — интрига пока сохраняется.
На
Не претендуя на лавры Мотидзуки, я
Кому интересно что получилось, прошу под кат.
Постановка задачи
Начнем с начала. О чем собственно, теорема? Как гласит Википедия (формулировка в английской версии немного более понятна), для взаимно-простых (не имеющих общих делителей) чисел a, b и с, таких что a+b=c, для любого ε>0 существует ограниченное число троек a+b=c, таких что:
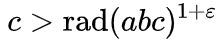
Функция rad называется радикалом, и обозначает произведение простых множителей числа. Например, rad(16) = rad(2*2*2*2) = 2, rad(17) = 17 (17 простое число), rad(18) = rad(2*3*3) = 2*3 = 6, rad(1000000) = rad(2^6 ⋅ 5^6) = 2*5 = 10.
Собственно, суть теоремы в том, что количество таких троек довольно мало. Например, если взять наугад ε=0.2 и равенство 100+27=127: rad(100) = rad(2*2*5*5) = 10, rad(27)=rad(3*3*3)=3, rad(127) = 127, rad(a*b*c) = rad(a)*rad(b)*rad(с) = 3810, 3810^1.2 явно больше 127, неравенство не выполняется. Но бывают и исключения, например для равенства 49 + 576 = 625 условие теоремы выполняется (желающие могут проверить самостоятельно).
Следующий ключевой для нас момент — этих равенств, согласно теореме, ограниченное число. Т.е. это значит, что их все можно просто попытаться перебрать на компьютере. В итоге, это дает нам
Итак, приступим.
Исходный код
Первая версия была написана на Python, и хотя этот язык слишком медленный для подобных расчетов, писать код на нем легко и просто, что удобно для прототипирования.
Получение радикала: раскладываем число на простые множители, затем убираем повторы, преобразуя массив в множество. Затем просто получаем произведение всех элементов.
def prime_factors(n):
factors = []
# Print the number of two's that divide n
while n % 2 == 0:
factors.append(int(2))
n = n / 2
# n must be odd at this point so a skip of 2 ( i = i + 2) can be used
for i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide n
while n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2
if n > 2:
factors.append(int(n))
return set(factors)
def rad(n):
result = 1
for num in prime_factors(n):
result *= num
return result
Взаимно-простые числа: раскладываем числа на множители, и просто проверяем пересечение множеств.
def not_mutual_primes(a,b,c):
fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c)
return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
Проверка: используем уже созданные функции, тут все просто.
def check(a,b,c):
S = 1.2 # Eps=0.2
if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c):
print("{} + {} = {} - PASSED".format(a, b, c))
else:
print("{} + {} = {} - FAILED".format(a, b, c))
check(10, 17, 27)
check(49, 576, 625)
Желающие могут поэкспериментировать самостоятельно, скопировав вышеприведенный код в любой онлайн-редактор языка Python. Разумеется, код работает ожидаемо медленно, и перебор всех троек хотя бы до миллиона был бы слишком долгим. Ниже под спойлером есть оптимизированная версия, рекомендуется использовать ее.
Окончательная версия была переписана на С++ с использованием многопоточности и некоторой оптимизации (работать на Си с пересечением множеств было бы слишком хардкорно, хотя вероятно и быстрее). Исходный код под спойлером, его можно скомпилировать в бесплатном компиляторе g++, код работает под Windows, OSX и даже на Raspberry Pi.
Код на С++
// To compile: g++ abc.cpp -O3 -fopenmp -oabc
#include <string.h>
#include <math.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdio.h>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <time.h>
typedef unsigned long int valType;
typedef std::vector<valType> valList;
typedef std::set<valType> valSet;
typedef valList::iterator valListIterator;
std::vector<valList> valFactors;
std::vector<double> valRads;
valList factors(valType n) {
valList results;
valType z = 2;
while (z * z <= n) {
if (n % z == 0) {
results.push_back(z);
n /= z;
} else {
z++;
}
}
if (n > 1) {
results.push_back(n);
}
return results;
}
valList unique_factors(valType n) {
valList results = factors(n);
valSet vs(results.begin(), results.end());
valList unique(vs.begin(), vs.end());
std::sort(unique.begin(), unique.end());
return unique;
}
double rad(valType n) {
valList f = valFactors[n];
double result = 1;
for (valListIterator it=f.begin(); it<f.end(); it++) {
result *= *it;
}
return result;
}
bool not_mutual_primes(valType a, valType b, valType c) {
valList res1 = valFactors[a], res2 = valFactors[b], res3; // = valFactors[c];
valList c12, c13, c23;
set_intersection(res1.begin(),res1.end(), res2.begin(),res2.end(), back_inserter(c12));
if (c12.size() != 0) return false;
res3 = valFactors[c];
set_intersection(res1.begin(),res1.end(), res3.begin(),res3.end(), back_inserter(c13));
if (c13.size() != 0) return false;
set_intersection(res2.begin(),res2.end(), res3.begin(),res3.end(), back_inserter(c23));
return c23.size() == 0;
}
int main()
{
time_t start_t, end_t;
time(&start_t);
int cnt=0;
double S = 1.2;
valType N_MAX = 10000000;
printf("Getting prime factors...\n");
valFactors.resize(2*N_MAX+2);
valRads.resize(2*N_MAX+2);
for(valType val=1; val<=2*N_MAX+1; val++) {
valFactors[val] = unique_factors(val);
valRads[val] = rad(val);
}
time(&end_t);
printf("Done, T = %.2fs\n", difftime(end_t, start_t));
printf("Calculating...\n");
#pragma omp parallel for reduction(+:cnt)
for(int a=1; a<=N_MAX; a++) {
for(int b=a; b<=N_MAX; b++) {
int c = a+b;
if (c > pow(valRads[a]*valRads[b]*valRads[c], S) && not_mutual_primes(a,b,c)) {
printf("%d + %d = %d\n", a,b,c);
cnt += 1;
}
}
}
printf("Done, cnt=%d\n", cnt);
time(&end_t);
float diff_t = difftime(end_t, start_t);
printf("N=%lld, T = %.2fs\n", N_MAX, diff_t);
}
Для тех кому лень устанавливать компилятор С++, приведена слегка оптимизированная Python-версия, запустить которую можно в любом онлайн редакторе (я использовал https://repl.it/languages/python).
Python-версия
from __future__ import print_function
import math
import time
import multiprocessing
prime_factors_list = []
rad_list = []
def prime_factors(n):
factors = []
# Print the number of two's that divide n
while n % 2 == 0:
factors.append(int(2))
n = n / 2
# n must be odd at this point so a skip of 2 ( i = i + 2) can be used
for i in range(3, int(math.sqrt(n)) + 1, 2):
# while i divides n , print i ad divide n
while n % i == 0:
factors.append(int(i))
n = n / i
# Condition if n is a prime number greater than 2
if n > 2:
factors.append(int(n))
return factors
def rad(n):
result = 1
for num in prime_factors_list[n]:
result *= num
return result
def not_mutual_primes(a,b,c):
fa, fb, fc = prime_factors_list[a], prime_factors_list[b], prime_factors_list[c]
return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
def calculate(N):
S = 1.2
cnt = 0
for a in range(1, N):
for b in range(a, N):
c = a+b
if c > (rad_list[a]*rad_list[b]*rad_list[c])**S and not_mutual_primes(a, b, c):
print("{} + {} = {}".format(a, b, c))
cnt += 1
print("N: {}, CNT: {}".format(N, cnt))
return cnt
if __name__ == '__main__':
t1 = time.time()
NMAX = 100000
prime_factors_list = [0]*(2*NMAX+2)
rad_list = [0]*(2*NMAX+2)
for p in range(1, 2*NMAX+2):
prime_factors_list[p] = set(prime_factors(p))
rad_list[p] = rad(p)
calculate(NMAX)
print("Done", time.time() - t1)
Результаты
Троек a,b,c действительно очень мало.
Некоторые результаты приведены ниже:
N=10: 1 «тройка», время выполнения <0.001c
1 + 8 = 9
N=100: 2 «тройки», время выполнения <0.001c
1 + 8 = 9
1 + 80 = 81
N=1000: 8 «троек», время выполнения <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N=10000: 23 «тройки», время выполнения 2с
Тройки A,B,C до 10000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
3 + 125 = 128
5 + 1024 = 1029
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
49 + 576 = 625
1331 + 9604 = 10935
81 + 1250 = 1331
125 + 2187 = 2312
243 + 1805 = 2048
289 + 6272 = 6561
625 + 2048 = 2673N=100000: 53 «тройки», время выполнения 50c
Тройки A,B,C до 100000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
49 + 576 = 625
49 + 16335 = 16384
73 + 15552 = 15625
81 + 1250 = 1331
121 + 12167 = 12288
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
1331 + 9604 = 10935
1625 + 16807 = 18432
28561 + 89088 = 117649
28561 + 98415 = 126976
3584 + 14641 = 18225
6561 + 22000 = 28561
7168 + 78125 = 85293
8192 + 75843 = 84035
36864 + 41261 = 78125При N=1000000 имеем всего лишь 102 «тройки», полный список приведен под спойлером.
Тройки A,B,C до 1000000
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
1 + 137780 = 137781
1 + 156249 = 156250
1 + 229375 = 229376
1 + 263168 = 263169
1 + 499999 = 500000
1 + 512000 = 512001
1 + 688127 = 688128
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
5 + 177147 = 177152
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
13 + 421875 = 421888
17 + 140608 = 140625
25 + 294912 = 294937
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
43 + 492032 = 492075
47 + 250000 = 250047
49 + 576 = 625
49 + 16335 = 16384
49 + 531392 = 531441
64 + 190269 = 190333
73 + 15552 = 15625
81 + 1250 = 1331
81 + 123823 = 123904
81 + 134375 = 134456
95 + 279841 = 279936
121 + 12167 = 12288
121 + 255879 = 256000
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
128 + 109375 = 109503
128 + 483025 = 483153
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
338 + 390625 = 390963
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
864 + 923521 = 924385
1025 + 262144 = 263169
1331 + 9604 = 10935
1375 + 279841 = 281216
1625 + 16807 = 18432
2197 + 583443 = 585640
2197 + 700928 = 703125
3481 + 262144 = 265625
3584 + 14641 = 18225
5103 + 130321 = 135424
6125 + 334611 = 340736
6561 + 22000 = 28561
7153 + 524288 = 531441
7168 + 78125 = 85293
8192 + 75843 = 84035
8192 + 634933 = 643125
9583 + 524288 = 533871
10816 + 520625 = 531441
12005 + 161051 = 173056
12672 + 117649 = 130321
15625 + 701784 = 717409
18225 + 112847 = 131072
19683 + 228125 = 247808
24389 + 393216 = 417605
28561 + 89088 = 117649
28561 + 98415 = 126976
28561 + 702464 = 731025
32768 + 859375 = 892143
296875 + 371293 = 668168
36864 + 41261 = 78125
38307 + 371293 = 409600
303264 + 390625 = 693889
62192 + 823543 = 885735
71875 + 190269 = 262144
131072 + 221875 = 352947
132651 + 588245 = 720896
Увы, программа работает все равно медленно, результатов для N=10000000 я так и не дождался, время вычисления составляет больше часа (возможно я где-то ошибся с оптимизацией алгоритма, и можно сделать лучше).
Еще интереснее посмотреть результаты графически:

В принципе, вполне очевидно, что зависимость количества возможных троек от N растет заметно медленнее самого N, и вполне вероятно, что результат будет сходиться к какому-то конкретному числу для каждого ε. Кстати, при увеличении ε число «троек» заметно сокращается, например при ε=0.4 имеем всего 2 равенства при N<100000 (1 + 4374 = 4375 и 343 + 59049 = 59392). Так что в целом, похоже что теорема действительно выполняется (ну и наверное ее уже проверяли на компьютерах помощнее, и возможно, все это уже давно посчитано).
Желающие могут поэкспериментировать самостоятельно, если у кого будут результаты для чисел 10000000 и выше, я с удовольствием добавлю их к статье. Разумеется, было бы интересно «досчитать» до того момента, когда множество «троек» совсем перестанет расти, но это может занять реально долгое время, скорость расчета похоже зависит от N как N*N (а может и N^3), и процесс весьма долгий. Но тем не менее, удивительное рядом, и желающие вполне могут присоединиться к поиску.
Правка: как подсказали в комментариях, в Википедии таблица с результатами уже есть — в диапазоне N до 10^18 количество «троек» все же растет, так что «конец» множества пока не найден. Тем интереснее — интрига пока сохраняется.