Интереснейшую реализацию шахматной программы показали вчера на Хабре.
Почитав комментарии, я пришел к выводу, что принцип работы наиболее распространенных алгоритмов игры в шахматы, шашки и тому подобные известны не всем.
Вместе с тем задача создания программы, играющей во что-то, достаточно тривиальна, если имеются способы расчета некоторых величин и оценок, специфичных именно для этой игры.
Расскажу об альфа-бета-отсечениях и минимаксном методе применительно к шахматам (в литературе можно также встретить более общие термины «метод граней и оценок» и «метод ветвей и границ»)
В любой момент игры для каждого игрока существует некоторое число допустимых правилами ходов. Допустим, оно конечно. В ответ второй игрок тоже может сделать некоторое конечное число ходов. Если исключить возможность зацикливания игры, то общее число позиций и переходов между ними велико, но конечно. Шахматные правила именно таковы.
Казалось бы, что проще: выполнили полный перебор и мы знаем все про игру; компьютер не сможет проиграть.
Однако число позиций столь велико, что полный анализ игры практически невозможен (за исключением классических крестиков-ноликов 3х3 и аналогичных по богатству стратегий игр).
Поэтому на практике делается следующее:
1. Аналитически, экспертно или методом рассуждений по прецедентам строится функция оценки позиции на доске. Эту оценку обычно ранжируют на оси: чем больше она, тем выгоднее белым, чем меньше, тем выгоднее черным и соответственно невыгоднее белым (так называемые игры с нулевой суммой).
2. Строится неполное дерево ходов. При этом число обсчитываемых полуходов реально определяется имеющимися вычислительными ресурсами (приложенная программа обсчитывает 7 полуходов, что довольно скромно для современных программ)
3. Выполняется некоторый в меру интеллектуальный анализ дерева возможных ходов, в процессе которого отсекаются заведомо неоптимальные ветки и глубоко просчитываются более перспективные. Как раз тут и выполняется знаменитая альфа-бета-процедура.
А теперь то же самое, но более формально и строго (изложение в основном базируется на статье Д.Кнута и Р.Мура в переводе Павла Дубнера):
Обозначения:
p – позиция
f(p) – численная функция, оценивающая выигрыш «нашего» игрока в конце игры (эти положения р называют еще терминальными)
F(p) – численная функция, оценивающая выигрыш «нашего» игрока в нетерминальной позиции
Будем исходить из того, что второй игрок действует тоже лучшим для себя образом.
Тогда:
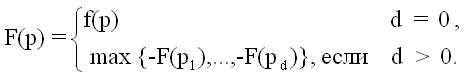
Тут есть тонкое соображение, Кнут с Муром его прекрасно сформулировали, поэтому просто процитирую:
Полный поиск в глубину:
Этот поиск рекурсивен и будет работать очень долго, зато гарантированно найдет оптимальную стратегию.
Можно оптимизировать алгоритм, не рассматривая те ветви дерева ходов, которые заведомо хуже уже найденного решения (это и называется методом ветвей и границ).
Идею метода ветвей и границ реализует следующий алгоритм:
Эта модификация тоже находит оптимальное решение.
В случае анализа заведомо конечного игрового дерева, где все терминальные вершины имеют оценки, можно ввести не только верхнюю границу для поиска, но и нижнюю, еще сократив пространство поиска и сэкономив ресурсы.
Альфа-бета-отсечения реализуются следующим кодом:
Такая оптимизация все еще находит заведомо лучшее решение.
На практике даже в самых простых играх, не говоря даже о шахматах, полный перебор терминальных позиций организовать нельзя. Поэтому встает нетривиальная задача примерной оценки позиции. Понятно, что верный мат дает много плюсов к позиции, но также учитывается все: положение фигур, защищенность короля, численный перевес, возможность рокировок. В зависимости от деталей реализации робот может оказаться слишком осторожным или, напротив, безрассудно кидающимся в размены.
Использование любых функций оценки лишает алгоритм математической строгости. Он будет настолько хорош, насколько хороша функция оценки.
Понятно, что первый вызов функции F2 содержит в качестве alpha и beta бесконечности разного знака.
Пример дерева ходов:

Дополнительные пояснения по последнему рисунку тут: Источник
Еще одна проблема – начало партии. До конца далеко, перспективы туманны, детские маты никто не дает ставить. Поэтому, как правило, используются библиотеки исследованных дебютов. Если же соперник делает нечто невразумительное с позиций шахматной тактики, включается описанный выше анализатор.
В принципе, все вышеописанное относительно несложно. Мои студенты после 2 курса втроем за три недели сваяли вот эти шахматы. Там все сделано достаточно качественно и есть куда расти.
Почитав комментарии, я пришел к выводу, что принцип работы наиболее распространенных алгоритмов игры в шахматы, шашки и тому подобные известны не всем.
Вместе с тем задача создания программы, играющей во что-то, достаточно тривиальна, если имеются способы расчета некоторых величин и оценок, специфичных именно для этой игры.
Расскажу об альфа-бета-отсечениях и минимаксном методе применительно к шахматам (в литературе можно также встретить более общие термины «метод граней и оценок» и «метод ветвей и границ»)
В любой момент игры для каждого игрока существует некоторое число допустимых правилами ходов. Допустим, оно конечно. В ответ второй игрок тоже может сделать некоторое конечное число ходов. Если исключить возможность зацикливания игры, то общее число позиций и переходов между ними велико, но конечно. Шахматные правила именно таковы.
Казалось бы, что проще: выполнили полный перебор и мы знаем все про игру; компьютер не сможет проиграть.
Однако число позиций столь велико, что полный анализ игры практически невозможен (за исключением классических крестиков-ноликов 3х3 и аналогичных по богатству стратегий игр).
Поэтому на практике делается следующее:
1. Аналитически, экспертно или методом рассуждений по прецедентам строится функция оценки позиции на доске. Эту оценку обычно ранжируют на оси: чем больше она, тем выгоднее белым, чем меньше, тем выгоднее черным и соответственно невыгоднее белым (так называемые игры с нулевой суммой).
2. Строится неполное дерево ходов. При этом число обсчитываемых полуходов реально определяется имеющимися вычислительными ресурсами (приложенная программа обсчитывает 7 полуходов, что довольно скромно для современных программ)
3. Выполняется некоторый в меру интеллектуальный анализ дерева возможных ходов, в процессе которого отсекаются заведомо неоптимальные ветки и глубоко просчитываются более перспективные. Как раз тут и выполняется знаменитая альфа-бета-процедура.
А теперь то же самое, но более формально и строго (изложение в основном базируется на статье Д.Кнута и Р.Мура в переводе Павла Дубнера):
Обозначения:
p – позиция
f(p) – численная функция, оценивающая выигрыш «нашего» игрока в конце игры (эти положения р называют еще терминальными)
F(p) – численная функция, оценивающая выигрыш «нашего» игрока в нетерминальной позиции
Будем исходить из того, что второй игрок действует тоже лучшим для себя образом.
Тогда:
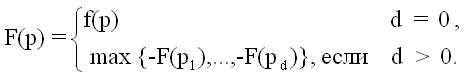
Тут есть тонкое соображение, Кнут с Муром его прекрасно сформулировали, поэтому просто процитирую:
Следует, однако, заметить, что она отражает результаты весьма осторожной стратегии, которая не обязательно хороша против плохих игроков или игроков, действующих согласно другому принципу оптимальности. Пусть, например, имеются два хода в позиции p1 и p2, причем p1 гарантирует ничью (выигрыш 0) и не дает возможности выиграть, в то время, как p2 дает возможность выиграть, если противник просмотрит очень тонкий выигрывающий ход. В такой ситуации мы можем предпочесть рискованный ход в p2, если только мы не уверены в том, что наш противник всемогущ и всезнающ. Очень возможно, что люди выигрывают у шахматных программ таким именно образом.
Полный поиск в глубину:
int F(void *p)
{
int res,i,t,d,m;
// получаем список возможных ходов ps (их число равно d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;i<=d;i++)
{
t = -F(ps[i]);
if (t > m) m=t;
}
res = m;
}
return res
* This source code was highlighted with Source Code Highlighter.Этот поиск рекурсивен и будет работать очень долго, зато гарантированно найдет оптимальную стратегию.
Можно оптимизировать алгоритм, не рассматривая те ветви дерева ходов, которые заведомо хуже уже найденного решения (это и называется методом ветвей и границ).
Идею метода ветвей и границ реализует следующий алгоритм:
int F1(void *p, int bound)
{
int res,i,t,d,m;
// получаем список возможных ходов ps (их число равно d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;(i<=d) && (m<bound);i++)
{
t = -F1(ps[i],-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter.Эта модификация тоже находит оптимальное решение.
В случае анализа заведомо конечного игрового дерева, где все терминальные вершины имеют оценки, можно ввести не только верхнюю границу для поиска, но и нижнюю, еще сократив пространство поиска и сэкономив ресурсы.
Альфа-бета-отсечения реализуются следующим кодом:
int F1(void *p, int alpha, int beta)
{
int res,i,t,d,m;
// получаем список возможных ходов ps (их число равно d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = alpha;
for (i=1;(i<=d) && (m<beta);i++)
{
t = -F2(ps[i],-beta,-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter.Такая оптимизация все еще находит заведомо лучшее решение.
На практике даже в самых простых играх, не говоря даже о шахматах, полный перебор терминальных позиций организовать нельзя. Поэтому встает нетривиальная задача примерной оценки позиции. Понятно, что верный мат дает много плюсов к позиции, но также учитывается все: положение фигур, защищенность короля, численный перевес, возможность рокировок. В зависимости от деталей реализации робот может оказаться слишком осторожным или, напротив, безрассудно кидающимся в размены.
Использование любых функций оценки лишает алгоритм математической строгости. Он будет настолько хорош, насколько хороша функция оценки.
Понятно, что первый вызов функции F2 содержит в качестве alpha и beta бесконечности разного знака.
Пример дерева ходов:

Дополнительные пояснения по последнему рисунку тут: Источник
Еще одна проблема – начало партии. До конца далеко, перспективы туманны, детские маты никто не дает ставить. Поэтому, как правило, используются библиотеки исследованных дебютов. Если же соперник делает нечто невразумительное с позиций шахматной тактики, включается описанный выше анализатор.
В принципе, все вышеописанное относительно несложно. Мои студенты после 2 курса втроем за три недели сваяли вот эти шахматы. Там все сделано достаточно качественно и есть куда расти.