Comments 22
Похоже на какую-то изощренную первоапрельскую шутку :)
Мне кажется, на элемент цепочки будут действовать три силы: две силы натяжения, и сила тяжести. И именно из-за потери силы тяжести, у Вас получилось, что движение не зависит от удельной массы.
Так не зависит же.
Проведите мысленный эксперимент: повесьте рядом две цепочки, качните одинаково. Колебаться будут, как одна. Теперь объединяем их – и получаем цепочку с вдвое большей удельной массой, колеблющуюся так же.
В случае с жётским маятником в формуле массы нет: только длина и ускорение падения. После этого — неудивительно.
Ровно по той же причине, по которой все тела в поле силы тяжести падают одинаково: сила тяжести пропорциональна массе, но массе пропорциональна и инерция.
Здесь, в отличие от ЖЁСТКОГО маятника, ситуация гораздо интереснее.
С одной стороны, на фоне двух других сил составляющая силы тяжести g*dm очень мала, с другой стороны, содбираясь в интеграл, они могут дать заметный вклад в поведение цепочки.
С натурным экспериментом сравнивали? Что-то у меня плохие предчувствия для реальности...
Я как-то задался вопросом, какой функцией описывается форма цепи в поле тяжести, точка подвеса которой вращается в горизонтальной плоскости (думаю, каждый представляет себе куполообразную поверхность, описываемую такой цепочкой). Решать я так и не взялся, но, прочитав статью, заподозрил, что там в решении тоже будут функции Бесселя. Спасибо)
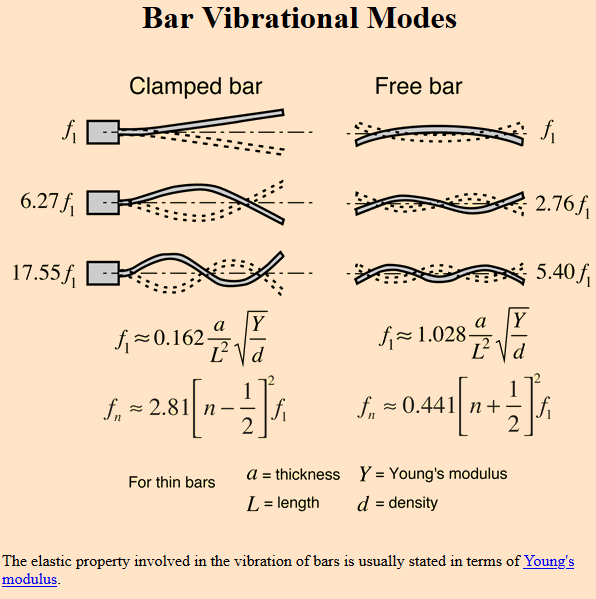
Интересно было бы рассмотреть какую-нибудь систему, в которой частоты колебательных мод расположены непериодично. В реальном мире из всех упругих тел гармоническим спектром обладает только тонкая струна. Более массивные тела (например, стержни, пластины, трубки, колокола) имеют сложный негармонический спектр. Есть ли аналитические решения для колебаний таких предметов?
(Пример взят с сайта: hyperphysics.phy-astr.gsu.edu/hbase/Music/barres.html)
Для цепочки, необходимо учитывать наличие жестких элементов не пренебрежимой длины, и их взаимодействие между собой
Вы думаете что вы решаете задачу по физике? НЕТ! Вы придумали математическое оправдание того, как по вашему собственному мнению будет колебаться цепочка. А смысла в вашей задаче нет ни какого, т.к. цепочка будет колебаться не так как вы сами себе придумали, а так как она будет колебаться на «самом деле» — (т.е. совсем иначе).
Ваше решение основано и начинается со Второго закона Ньютона. А вы можете написать формулу этого Закона и объяснить его смысл? Думаю что вы не знаете о чем данный закон! Так чего вы тут решаете?
Ну что ж, процитирую концовку статьи:
«Сравните это выражение с периодом колебаний математического маятника.
На этом наше исследование колебаний свободно висящей цепочки окончено.»
С чем сравнить! А что: в природе есть «математический маятник» ???
А что можно что то сравнить с тем чего НЕТ? Вам самим не смешно от вашего невежества?
«Математический маятник» — это математическое допущение = ПРИДУМКА = ВЫМЫСЕЛ! Которую придумали математики для себя любимых, чтобы они могли решать математические уравнения и при этом пренебрегать силами трения и сопротивления. Это не имеет к Физике вообще ни какого отношения, т.к. Физика изучает природные явления, а не математический БРЕД!
А называть математические выдумки «Исследованиями» — это крайняя степень шизофрении.
Рассказ о «цепочке Лагранжа» www.sakharov-center.ru/asfcd/auth/?t=page&num=2133
Задача о свободно висящей цепочке