Изобретаем JPEG
28 мин
Туториал

Вы правильно поняли из названия, что это не совсем обычное описание алгоритма JPEG (формат файла я подробно описывал в статье «Декодирование JPEG для чайников»). В первую очередь, выбранный способ подачи материала предполагает, что мы ничего не знаем не только о JPEG, но и о преобразовании Фурье, и кодировании Хаффмана. И вообще, мало что помним из лекций. Просто взяли картинку и стали думать как же ее можно сжать. Поэтому я попытался доступно выразить только суть, но при которой у читателя будет выработано достаточно глубокое и, главное, интуитивное понимание алгоритма. Формулы и математические выкладки — по самому минимуму, только те, которые важны для понимания происходящего.
Знание алгоритма JPEG очень полезно не только для сжатия изображений. В нем используется теория из цифровой обработки сигналов, математического анализа, линейной алгебры, теории информации, в частности, преобразование Фурье, кодирование без потерь и др. Поэтому полученные знания могут пригодиться где угодно.
Если есть желание, то предлагаю пройти те же этапы самостоятельно параллельно со статьей. Проверить, насколько приведенные рассуждения подходят для разных изображений, попытаться внести свои модификации в алгоритм. Это очень интересно. В качестве инструмента могу порекомендовать замечательную связку Python + NumPy + Matplotlib + PIL(Pillow). Почти вся моя работа (в т. ч. графики и анимация), была произведена с помощью них.
Внимание, трафик! Много иллюстраций, графиков и анимаций (~ 10Мб). По иронии судьбы, в статье про JPEG всего 2 изображения с этим форматом из полусотни.


 При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».
При решении такой задачи классифицируемые элементы (далее образцы) представляются в виде элементов векторного пространства размерности n. На практике в таких задачах n может быть чрезвычайно большим, например для задачи классификации генов оно может исчисляться десятками тысяч. Большая размерность влечёт, по-мимо высокого времени вычисления, потенциально высокую погрешность численных рассчётов. Кроме того использование большой размерности может требовать больших финансовых затрат (на проведение опытов). Постановка вопроса такова: можно ли и как уменьшить n отбрасыванием незначимых компонент образцов так, чтобы образцы разделялись «не хуже» в новом пространстве (оставались линейно разделимы) или «не сильно хуже».
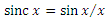 (ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:
(ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке: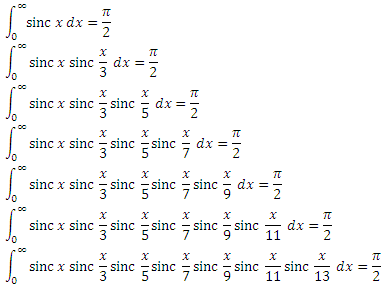






 (с) xkcd
(с) xkcd