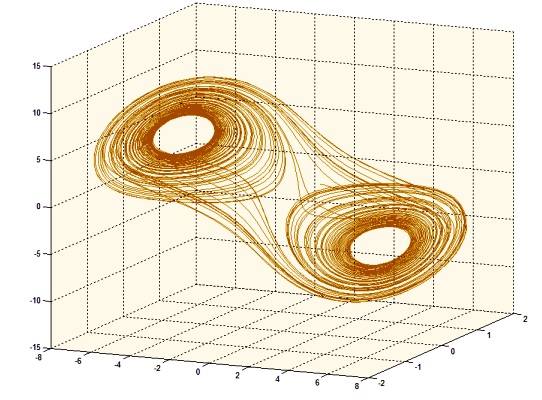
Задайтесь вопросом «ГДЕ?». Где находится центр управления движением галактик или поведением циклона? Где та сила, что объединяет атомы в сложные соединения, те в свою очередь — в цепочки белков, и порождает такие устойчивые и сложные явления как биологическая жизнь, разум, социум.

Под зонтиком теории сложности объединены разнообразные модели, которые описывают, как без центрального контроля из взаимодействия простых начальных элементов, подчиняющихся простым правилам, образуются явления более высокого порядка, обладающие сложно предсказуемым поведением и непредвиденными, но устойчивыми, свойствами.
Статья не предлагает готовых ответов о смысле жизни, сквозит грубыми нестрогими аналогиями, но при этом имеет дерзкую цель расширить кругозор читателя, опираясь на его воображение и некоторые математические факты.

Несмотря на закрытие многих коворкинг-центров первой волны и постоянные заявления о неприбыльности, коворкинг движение живее всех живых. По данным ведущего коворкинг издания DeskMag, только с мая по ноябрь 2011 года число коворкинг-центров в мире увеличилось с 820 до 1100. Россия не отстает, и новые места продолжают открываться.

Зона действия (Санкт-Петербург)

Из комментариев к предыдущей статье кроме кучи полезной информации, обсуждения недостатков моего кода, я вынес ещё и стратегическое решение — всеми правдами и неправдами избегать программирования на C/C++ на ближайшем интервью. Сказывается отсутствие практики написания программ. Уже больше 4х лет его не трогал и питона хватало для любых статистических вычислений и визуализации данных. Но обязательно вернусь к классическим учебникам на следующей недели. Товарищи TheHorse и 0leGG застыдили меня во второй статьe, а AxisPod забил последний гвоздик в гробик моих надежд, что получится выехать на старых знаниях. Поэтому смещая акцент именно в сторону любимого Python, посмотрим на возможные задачи.

Сегодня мы будет обсуждать технические аспекты и реализацию задач на Python и C/C++, которыми нас будет закидывать инженер из Google. Начнём с самых тривиальных проблем с последующим нарастанием сложности. Параллельно обратим внимание о чём стоит упомянуть во время интервью и где не попасть в ловушку.

Вероятно многие встречались с таким вот «партизаном» при старте или завершении приложения:



Очень информативное сообщение, сразу понятна причина ошибки, место и способ ее решения.
Впрочем, если без шуток, что это вообще такое?
Конечно-же это исключение, но ни тип исключения, ни его описание нам не доступны — просто «Runtime error 217» и адрес, а дальше сами…

Если честно, раньше я как-то даже не задумывался по поводу данного исключения, т.к. в моих проектах оно явление редкое, пока однажды у целой череды пользователей не начала воспроизводится именно 217-я ошибка.
Впрочем, даже тогда я не пошел по правильному пути и просто добавил дополнительный уровень логирования в проект, по результатам которого достаточно оперативно нашел причину и исправил ее.
Но, по сути, я просто потратил свое время…

И тратил бы его в дальнейшем, если бы на днях со мной не связался Виктор Федоренков и не рассказал о своих мыслях по поводу ошибки за номером 217.

Проблема

Как обычно поздней ночью, садясь в автобус, я достал телефон, и пока набирал “habr…” он отрубился. Я вслух подумал: “А раньше не мог сказать?”, немного пожалел, что телефоны редко пищат, пока разряжаются. А потом…

Потом мы с приятелем решили подойти к вопросу по-мужски. Он написал программулину для андроида, а я расширил Хром. О последнем и пойдёт речь.

Задача

Итак, идея: андроид-приложение наблюдает за состоянием аккумулятора и периодически уведомляет сервер об уровне заряда. Причём делает это как-нибудь по-умному, чтобы заряд от этого не пострадал. Хром-расширение выставляет свою иконку в специально отведённом месте, иконка показывает заряд батарейки андроида и всячески привлекает внимание, если она совсем почти разряжена. А чтобы всё не казалось слишком простым, реализовать идею надо было за одни выходные. В противном случае баланс ценность/усилия вываливался за рамки бесплатного приложения.

Таким образом, выбор подхода к задаче оказался даже важнее скорости десятипальцевой печати.

Открытые вакансии на должность разработчика в Яндексе есть всегда. Компания развивается, и хороших программистов не хватает постоянно. И претендентов на эти должности тоже хоть отбавляй. Главная сложность – отобрать действительно подходящих кандидатов. И в этом плане Яндекс мало чем отличается от большинства крупных IT-компаний. Так что базовые принципы, описываемые в этой статье, могут быть применимы не только к Яндексу.

Однако стоит оговориться, что статья все же про подбор разработчиков. Т.е. собственно тех восьмидесяти процентов сотрудников, на которых держится массовая разработка. Часто мы нанимаем людей на специальные вакансии: например, разработчиков систем компьютерного зрения, лингвистов, экспертов по машинному обучению. В этом случае формат собеседования может заметно отличаться.

Предисловие

Одно время мне везло на всякие странные работы. Например, я чуть было не устроился админом в синагогу. Остановила меня только предчувствие, что меня там как последнего гоя будут заставлять работать по субботам.

Другой вариант тоже был любопытным. Фирма сочиняла эссе и курсовые для американских студентов, которым в лом было писать самим. Уже потом я узнал, что это довольно распространенный и прибыльный бизнес, которому даже придумали собственное название — «paper mill», но сразу такой способ зарабатывания на жизнь показался мне полным сюром. Однако же надо заметить, что интересных задач на этой работе оказалось немало и среди них — самая сложная и хитрая из тех, что я делал за свою карьеру, и которой можно потом с гордостью рассказывать детям.

Формулировка ее была очень проста. Сочинители курсовых — удаленные работники, очень часто — арабы и негры, для которых английский язык был неродным, и ленивы они были ничуть не меньше самих студентов. Нередко они шли по пути наименьшего сопротивления и вместо написания оригинальной работы тупо передирали ее из Интернета, целиком или частями. Соответственно, надо было найти источник (или источники), сравнить, как-то определить процент сплагиаченности и передать собранные сведения для уличения нерадивых.

Дело несколько облегчалось языком курсовых — он был исключительно английским, без падежей и сложных флективных форм; и сильно усложнялось тем, что непонятно было, с какой стороны вообще за это дело браться.

В качестве языка реализации был выбран Перл, что оказалось очень удачным. Ни на каком статическом компилируемом языке с их ригидностью и тормознутостью запуска решить эту задачу вообще было невозможно. Переписать готовое решение можно, а придти к нему путем многочисленных проб — никак нельзя. Ну и плюс куча отличных обкатанных библиотек.

Хоть проект не наш, но мы рады, то что процесс внедрения livecoding идет повсеместно. Один из авторов Unity уже больше года занимается созданием инструмента для «живого кодирования» для Unity. Сначала вышли версии для JS и Boo, а относительно недавно он выпустил Livity для C#!

На Хабре уже есть очень много интересных статей про создание игры с нуля, но мало статей, описывающих что делать, чтобы своя любимая поделка не превратилась во Франкенштейна и дошла до вменяемого состояния. Автор оригинальной статьи рассказывает, как эволюционировал код игрового движка от кучи хлама в основном цикле к продуманной, расширяемой архитектуре, использующей Entity Component System. В статье много кода, который почти весь часто повторяется — но я не стал его выбрасывать, поскольку с ним будет понятнее, какие изменения вносит автор и как это отражается на всей структуре. Статья рассчитана на новичков, вроде меня, которые уже настрочили несколько «гениальных» прототипов, но теперь не знают, как разобраться в их коде.

Предисловие

Как-то в гостях мне в руки попалась головоломка, в которой из 25 одинаковых фигурок требовалось собрать куб. Я провозился с ней почти весь вечер, и как можно догадаться, абсолютно безрезультатно. Тем не менее, я не мог сдаться просто так.

Не можешь сам — заставь компьютер. Сказано — сделано. В результате написанному по наитию алгоритму пришлось работать всю ночь, чтобы найти все 4 уникальных решения. В процессе гугления решений для сравнения, я нашёл программу Burr Tools, которая справилась с этой задачей за 3 минуты на моём ноутбуке.

Такая разница в скорости заставила меня разобраться, как решается эта задача и ещё целый класс подобных.

Решил однажды для себя я соорудить погодную станцию. Датчики там разные, в том числе на шине I2C. И как годится, обычно вначале, сделал все на флагах ожидания. Но путь настоящего джедая иной, и было решено все повесить на прерывания. Вот тут и начался геморрой. Проблема, с которой я столкнулся это обработка нескольких подряд идущих запросов. Например датчик давления BMP085 для дальнейшей работы с ним, требует вытянуть из его EEPROM 11 калибровочных констант:


О том как я пришел к решению и последовательность хода мыслей изложены ниже.

Для всех, кто хотел разобраться с Lua (скриптовый язык для разработки игр и не только, список), но никак не находил времени, Tyler Neylon приготовил небольшой подарок:

http://tylerneylon.com/a/learn-lua/

Посвящается всем, кто предпочитает один большой список из говорящих самих за себя сниппетов кода (с небольшими комментариями к 95% case'ов) длинным мануалам с огромной иерархией. Очень удобно для тех, кто уже умеет программировать и просто хотел бы разобраться с новым для себя языком. Весь «мега-сниппет» на английском, но примеры несложно читаются.

P.S. А для всего остального есть Hyperpolyglot.

В последнее время среди паттернов проектирования мобильных приложений наблюдается устойчивая тенденция к упрощению взаимодействия пользователя с конечным приложением. В частности, особый упор начал делаться на распознавание жестов. Жесты интуитивно понятны и естественны, они удобны и позволяют избавиться от лишних элементов интерфейса, упрощая приложение.

Хороший пример правильного использования жестов — набирающая популярность боковая навигация. На Хабре ранее публиковалась статья о боковой навигации как паттерне, но в ней ничего не было сказано о реализации.

К сожалению, проектов, реализующих боковую навигацию, крайне мало, да и большая часть из них работает медленно и неудобно. Мне повезло: спустя некоторое время после начала поиска я наткнулся на проект ActionsContentView, который, на мой взгляд, работал хорошо и быстро. В проекте были решены все те проблемы, с которым я столкнулся когда-то сам. После внимательного изучения проекта он был немного переписан мною под собственные нужды.

Изначально я хотел в этой статье расписать как и способ открытия бокового меню по клику, так и способ открытия меню жестом. Однако ближе к концу статьи стало очевидно, что обработка жестов и открытие навигации по ним достаточно объемный вопрос, в котором также следует учесть множество особенностей. Статья в таком случаем получается настолько огромная, что читать ее просто неудобно.
Поэтому я решил описать пока лишь реализацию бокового меню по клику.

На днях, после долгого перерыва, надо было поработать на WPF, и возникло желание заменить поднадоевший стандартный вид окон Windows 7 на что-нибудь более вдохновляющее, скажем в стиле Visual Studio 2012:

Часто замечаю, что большинство программистов, разрабатывающих приложения для Android, не в курсе последних новостей Android Community. Если о появлении новой версии ОС знают практически все, то выход различных полезных библиотек или интересных для разработчиков статей часто остается незамеченным.

За последний год у меня сформировался список контактов в соц. сетях наиболее известных личностей из Android Community. Эти люди регулярно пишут статьи, публикуют библиотеки, отвечают на StackOverflow и т.д. Подобный список помогает одному из первых узнавать новости сообщества Android Developers, поэтому решил поделиться им здесь.

^{Фото: Jay Mark Johnson}

Перед вами оригинальный снимок, без обработки в фоторедакторе или применения каких-то художественных эффектов. Исключительно точное документальное фото. Только это не картина одного момента, как в обычной фотографии. В кадре вместились события, которые происходили в течение около 30 секунд на промежутке пространства шириной 1 пиксел. Снимок сделан методом щелевой фотографии.

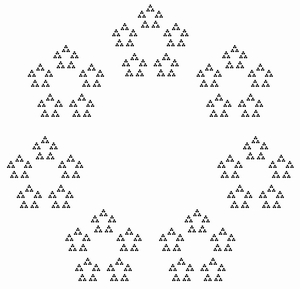Многие в общих чертах представляют, как работает обратная лучевая трассировка: через каждый пиксель окна вывода алгоритм пропускает луч и вычисляет, с какими объектами сцены он пересекается и как в результате данный пиксель должен быть освещён. Алгоритм по сути требует, чтобы у нас была функция, которая для каждой позиции возвращает цвет точки. Разумеется, тот же подход можно применять не только для трёхмерной графики: любое изображение можно растеризовать таким образом, если у нас есть подходящая функция. Рассмотрим для примера, как с помощью такого подхода решить задачу визуализации диаграмм разложения на простые множители, о которой написал helarqjsc.

Моя реализация здесь. На картинке изображено 10! = 3628800, хотя всех деталей, разумеется, не видно.

Недавно в свободное время написал программу для генерации диаграмм, полученных с помощью разложения числа на простые множители или "факторизационных диаграмм".

Вот так выглядит 700:


По расположению точек несложно заметить, что всего их здесь 7*5*5*2*2.

Далее описание того, как это работает.

Говоря «хаос», мы, обычно, подразумеваем полное отсутствие порядка, абсолютную неупорядоченность и случайность. С математической точки зрения, хаос и порядок – понятия не взаимоисключающие. Теория хаоса (есть что-то завораживающие в названиях математических теорий) – достаточно молодая математическая область, создание которой приравнивают по значимости открытий ХХ века к созданию квантовой механики. Хаос случается в нелинейных динамических системах. Иначе говоря, любой процесс, который протекает со временем, может быть хаотичным (например, высота дерева, температура тела или популяция мадагаскарских тараканов).