Вы когда-нибудь задумывались о том, что у человеческого мозга есть ограниченная емкость и вы можете выучить этот чертов английский просто потому что в детстве запомнили слишком много покемонов? Или почему обучение с учителем гораздо эффективнее, чем самостоятельное?
Эти вопросы вполне применимы и в области машинного обучения. Для обучения модели диффузии требуется много данных и вычислительной мощности, �� затем для создания изображений требуется значительное количество вычислений и серьезное оборудование. Исследователи (у которых обычно нет денег и на доширкак) задали очень хороший вопрос - можно ли достичь тех же результатов с меньшими усилиями?
Ответ - да. Есть простой трюк, который мы можем использовать - дистилляция модели.
Чтобы понять, как это работает, давайте сначала посмотрим на обычный процесс обучения модели.
Модели диффузии учатся генерировать данные, обращая процесс диффузии вспять, т.е. модель учится превращать случайный шум в согласованное изображение (обычно соотвествующее заданному промпту).
Обычно происходит что-то вроде этого:
мы берем кучу маркированных изображений и постепенно добавляем к ним шум в соответствии с графиком шума
затем мы обучаем модель предсказывать добавленный нами шум.
Во время вывода:
мы генерируем начальное изображение с чистым случайным шумом
модель предсказывает шум
мы постепенно удаляем предсказанный шум из начального случайного зашумленного изображения, используя данный запрос, и таким образом создаем конечное изображение.
Более подробное описание можно найти здесь.
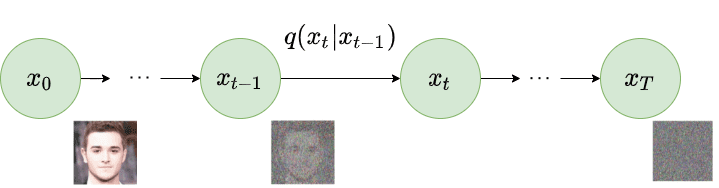
Визуально это выглядит следующим образом:


Проблема здесь в слове постепенно. Это требует сотен шагов, и каждый из них требует большого количества вычислений.
Почему мы делаем это таким образом? Ну, мы не можем просто перейти от шума к согласованному изображению, это привело бы к абстрактным сюрреалистическим результатам. Шум случаен и не содержит изображение как таковое (как правило). Постепенное удаление шума позволяет раскрыть общий контур изображения, который затем может быть детализирован шаг за шагом, используя предыдущие шаги в качестве базы. То же самое с людьми – вы не можете написать целое приложение на Python за один раз – обычно вы пишете код по частям, и он как бы эволюционирует.
Но почему нам нужно так много шагов? По-видимому, это больше результат начального математического описания проблемы, чем что-либо еще. Это напоминает мне, как часто формулировка проблемы и используемый язык диктуют решение.
Вот как это было постулировано:
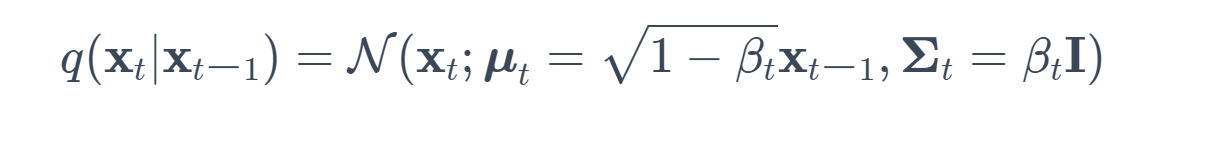
Изображение из статьи Denoising Diffusion Probabilistic Models.
Прямой процесс или процесс диффузии фиксируется в Марковской цепи, которая постепенно добавляет гауссовский шум к данным в соответствии с графиком дисперсии β1,...,βT. Учитывая точку данных x0, выбранную из реального распределения данных q(x) (x0∼q(x)), мы можем определить прямой процесс диффузии, добавляя шум. Конкретно, на каждом шаге мы добавляем гауссовский шум с дисперсией βt к xt−1, создавая новую скрытую переменную xt с распределением q(xt∣xt−1). Этот процесс диффузии может быть сформулирован следующим образом:
Этот процесс требует множества шагов для работы.
Вот и трюк. Мы берем модель, которая была обучена старым способом, используя миллионы долларов, и используем ее как учителя для обучения другой модели, которую мы называем учеником. Эта модель будет обучаться предсказывать не шум на изображении, а мы обучаем ее предсказывать следующий шаг родительской модели, используя среднеквадратичное отклонение между их результатами в качестве функции потерь и градиентного спуска. Эта модель все еще не особо эффективна, потому что мы все равно собираемся предсказывать то же количество шагов, что и родительская модель, и это потребует то же количество вычислительной мощности. Так как мы можем оптимизировать процесс?
Идея здесь в том, что мы не делаем это вышеописанным способом. Если подумать , а зачем нам предсказывать каждый шаг ??. Мы можем предсказывать каждый второй шаг, пропуская шаг в обучении и в выводе. Ученик больше не удаляет шум из случайного зашумленного изображения. Он удаляет шум из изображения, которое было обработано родительской моделью, а родительская модель уже обучена и знает, что делает (вот вам и польза учителей).
Таким образом, в модели ученика у нас будет вдвое меньше шагов, чем у родительской модели, и оказывается, что качество почти точно такое же. Затем мы берем эту модель ученика и используем ее в качестве учителя и создаем новую модель ученика. Затем мы обучаем нового ученика с использованием этой новой учительской модели и снова во время обучения пытаемся предсказывать только каждый второй шаг и так далее. В конце концов, мы повторяем этот процесс много раз, сжимая модель и количество шагов, уменьшая их вдвое каждый раз. Мы делаем этот процесс до тех пор, пока результаты нас перестают устраивать. Таким образом, мы эффективно сокращаем требования к вычислениям на каждой дистилляции наполовину, и на данный момент кажется, что можно иметь только четыре-шесть шагов, и модель все еще работает так же хорошо, как и начальная учительская модель с сотнями шагов. Это называется процессом дистилляции.
Вот диаграмма:
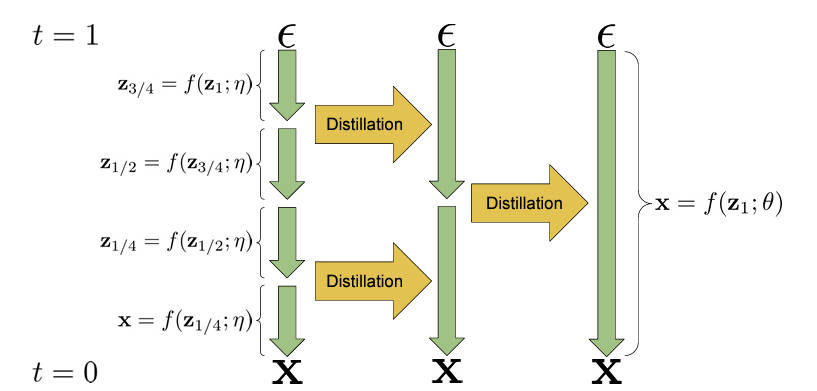
Визуализация двух итераций алгоритма прогрессивной дистилляции. Сэмплер f(z; η), отображающий случайный шум ε в образцы x в 4 детерминированных шагах, дистиллируется в новый сэмплер f(z; θ), выполняющий только один шаг.
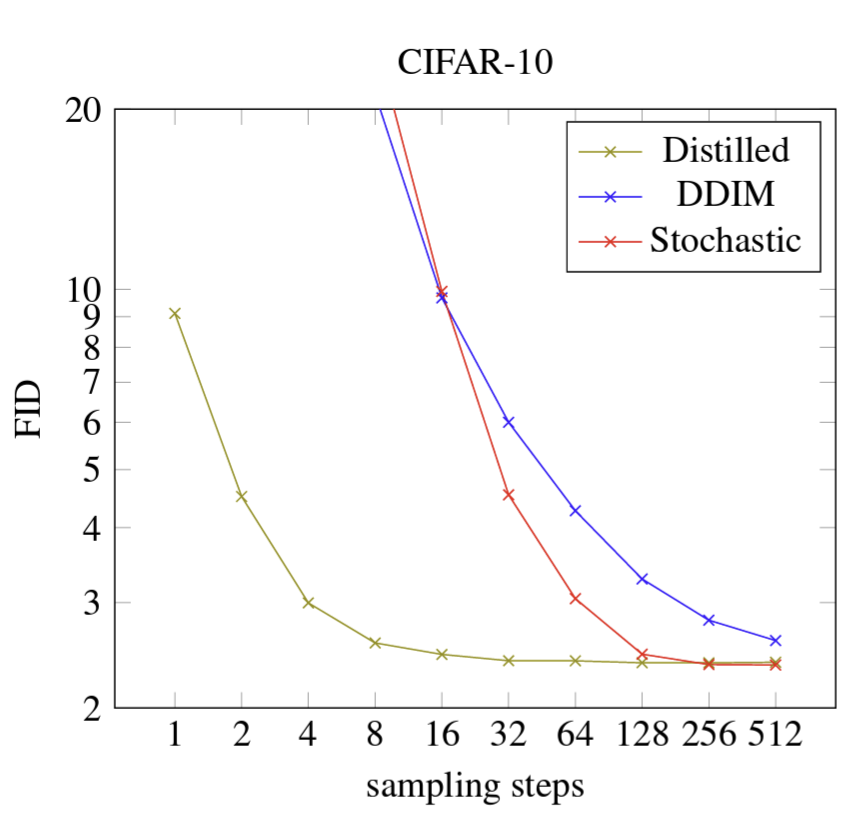
Как видно на диаграмме, дистиллированная модель имеет такое же качество всего за 8 шагов, как старая модель имеет за 256 шагов на наборе данных CIFAR-10.
Подход описан здесь: https://arxiv.org/abs/2202.00512.
Если у вас есть вопросы или предложения - пожалуйста, задавайте их в разделе комментариев.
Я со-основатель компании Рафт. Вот мой канал. Всем подписавшимся - теплое местечко в матрице гарантирую.