В прошлый раз мы разложили по полочкам вопросы про стоимость денег, типы процентов, дисконтирование и форвардные ставки, а сейчас распутаем клубок с облигациями: что это за инструмент, купонные и бескупонные, как рассчитать «чистую» и «грязную» цены. А также про рыночные соглашения, историю появления облигаций и откуда возникло выражение «стричь купоны».
В основе этого поста – две мои лекции из курса Finmath for Fintech, записи которых можно найти тут: «Облигации» и «Рыночные соглашения».
Облигация – это финансовый инструмент, по которому выплачивается на заранее оговоренную сумму в заранее оговоренные периоды времени какой-то процентный доход.
Рассмотрим, как будет выглядеть структура платежей по облигациям. Предположим, у нас есть трехлетняя облигация. При покупке облигации покупатель должен сделать платеж в размере номинала облигации. Пусть в нашем примере номинал облигации N составит 100 рублей. Регулярно будут производиться выплаты купонов по облигации. Купонный платеж измеряется в процентах. Предположим, что он равен пяти процентам (С=5%). В конце срока действия облигации (в момент погашения) держатель получает назад номинал и последний купонный платеж.
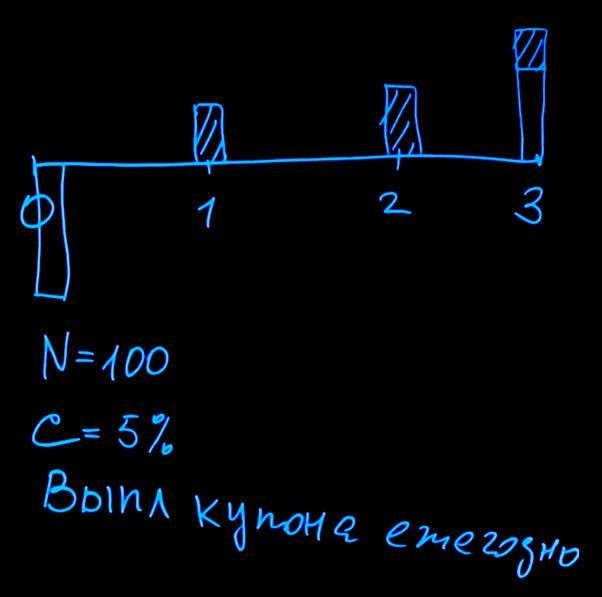
Выплаты купона, как показано на рисунке, происходят ежегодно. В принципе, эмитент облигации может назначать любую частоту выплат, например, ежеквартально или раз в полгода.
Есть также вид облигации, по которой купон не платится вообще – бескупонная облигация (Zero-coupon bond). Такая облигация покупается со скидкой от номинала (с дисконтом). Номинал этой облигации выплачивается при погашении, а в начале покупателем платится некоторая сумма, которая меньше номинала. Прибылью по такой облигации будет разница между ценой покупки облигации и номиналом этой облигации. Предположим, ее номинал сто рублей N=100, и дисконт по этой облигации составляет пять процентов d=5%, погашение через год. Согласно формуле дисконтирования, текущая стоимость облигации будет равна номиналу, дисконтированному по этой ставке в пять процентов.
PV=N/(1+d)=100/1,05=95,24 руб.
Это пример расчета справедливой цены самой простой облигации. Следует отметить, что если бескупонная облигация со сроком действия на год выпущена не сегодня, а, скажем, полгода назад, и мы хотим ее купить, цена облигации будет выше. Потому что за счет того, что уже прошло полгода, мы будем дисконтировать по меньшей процентной ставке, и, соответственно, облигация будет стоить дороже.
Срок действия по облигациям называется maturity. В момент maturity (выплаты номинала) стоимость облигации будет равняться ее номиналу, в нашем примере – ста рублям.
Давайте попробуем посчитать цену купонной облигации. Способ расчета будет очень похож на расчет бескупонной облигации. Вспомним, о чем говорилось ранее про дисконтирование: для того чтобы узнать стоимость облигации, нам нужно каждый купонный платеж привести к текущему моменту времени и просуммировать выплаты. Запишем это.
PV=C/(1+r1) + C/(1+r2)2 + (C+F)/(1+r3)3

Цена облигации будет состоять из трех частей: первый купон, дисконтированный по процентной ставке на один год, плюс второй купон, дисконтированный по процентной ставке на два года, и плюс последний купон, плюс номинал, или face value облигации, дисконтированный по процентной ставке на три года.
Рассмотрим, как будет выглядеть формула расчета цены облигации, если количество периодов начисления процентов не три, а больше. В общем виде мы получим сумму дисконтированных купонных доходов при значении n от единицы до T (количество периодов) плюс последняя выплата номинала нашей облигации, дисконтированная по ставке, которая действует на период времени T.
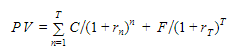
Как видите, не обязательно запоминать формулу расчета, ее легко можно вывести из общих соображений относительно того, какая структура платежей по данному продукту.
Одним из важных показателей облигации как инструмента является понятие доходности к погашению (Yield to Maturity). Это единая процентная ставка доходности облигации, которую получит держатель в том случае, если облигацию он держит до самого погашения, то есть ждет выплаты всех купонов и номинала в конце (а не продает ее в середине). Как определить эту доходность?
Для бескупонной облигации все достаточно просто – та ставка дисконта, с которой мы покупаем нашу облигацию, и будет являться доходностью к погашению. В нашем примере при покупке с дисконтом пять процентов доходность по облигации составит пять процентов. А как быть с купонной облигацией? Дело в том, что каждый купон дисконтируется по своей собственной ставке. Пока мы опустим, каким образом рассчитываются эти ставки (они рассчитываются исходя из текущих цен инструментов). Чтобы узнать доходность облигации к погашению, нужно, зная текущую цену облигации, вместо процентных ставок, по которым мы дисконтируем, подставить единую ставку. Решив уравнение n-ой степени, можно определить размер этой самой доходности.
Стоит также отметить, что важным фактором, влияющим на цену облигации, являются процентные ставки. Если мы держим облигацию до погашения, то на нас изменение процентных ставок никак не влияет, потому что нам не важно, как меняется текущая цена облигации, мы ее держим ради купонного дохода. Если же мы хотим облигацию продать в течение срока ее действия, то важно понимать, что изменение процентных ставок приводит к изменению цены облигации.
Так, если мы сегодня купили облигацию за сто рублей, то при росте процентных ставок цена облигации изменится, облигация будет стоить дешевле. Изменение процентных ставок и цены облигации обратны – если процентные ставки растут, цена облигации снижается, и наоборот (если процентные ставки снижаются, то цена облигации растет).
Как вы думаете, когда впервые появилась облигация? Честно говоря, когда я впервые узнала об этом финансовом инструменте, я думала, что это что-то, что было изобретено в XIX веке для торговли на американских биржах. Оказывается, первые облигации были изобретены шесть веков назад. Одним из первых эмитентов была Ост-Индская компания, которая занималась тем, что перевозила специи, и ей было даже совершено несколько крупных географических открытий. Это была крупнейшая компания своего времени, ее капитализация в пересчете на нынешние деньги составляла более семи триллионов долларов. Это больше, чем капитализация Apple и Google. Неудивительно, что такая огромная компания активно привлекала заемные средства на свои масштабные экспедиции. На изображении ниже вы можете видеть, как выглядели облигации этой компании от 1622 года.

Уже в девятнадцатом веке облигации использовались массово. Так, например, облигации выпускались Российской империей.
Все дело в том, что в XIX веке облигации выпускались на листе бумаги, который представлял из себя саму ценную бумагу и часть, на которой располагались купоны.

В каждом купоне указывался размер выплаты по этому купону и время, когда можно прийти и получить выплату. Для того, чтобы купон оплатили, необходимо было вырезать его из листа бумаги и предъявить. Владельцы облигаций стригли купоны и получали доход со своих вложений.
Кто может выпустить облигации? Ограничений нет, и эмитентом облигации может быть кто угодно. Облигации выпускают государства, городские муниципалитеты, коммерческие компании. Даже мелкие компании могут выпустить свои облигации. В зависимости от эмитента облигации будут иметь разное кредитное качество. Эту тему мы рассмотрим чуть ниже.
На рынке существуют определенные соглашения, которыми пользуются все его участники. При заключении сделок эти соглашения отдельно даже не оговариваются — это, своего рода, общее понимание. Касается оно и цен на облигации.
Цена облигации – это по сути процент от номинала облигации. Допустим, номинал облигации — тысяча или десять тысяч рублей. Если мы попросим продавца облигации назвать ее цену, он назовет цифры, например, 98, 100 или 105. Эти числа определяются процентами от номинала облигации, то есть цена облигации – это процент от ее номинала. Таким образом, если нам называют цену меньше ста, это означает, что облигация торгуется со скидкой (с дисконтом). Если облигацию нам продают за сто – означает, что ее продают по номиналу (Par Value). Ну, а если цена на облигацию оказывается выше ста, значит, она торгуется с премией.
Почему облигация может продаваться с дисконтом либо с премией? Если процентная ставка по купону выше существующих рыночных процентных ставок, то такая облигация скорее всего будет продаваться с премией, потому что это возможность для покупателя облигации заработать больший купонный доход, чем по другим существующим на рынках инструментам. Поэтому данная возможность закладывается в цену облигации, при приобретении покупатель платит больше, чем номинал.
Аналогично с дисконтированием. Если у нас получается, что процентная ставка по купону ниже, чем существующие на рынке процентные ставки, то покупателю будет предложена скидка от номинала облигации для того, чтобы он эту облигацию купил.
Еще одним важным рыночным соглашением на рынке облигаций является соглашение о подсчете дней (Day count convention). Вспомним формулу расчета цены облигации и обсудим, что же такое Day count convention.
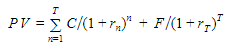
Цена облигации равняется сумме дисконтированных купонных платежей плюс дисконтированный номинал облигации. В частном случае, если у нас происходит начисление купонного дохода чаще, чем раз в год, то так как ставка rn выражена в годовом выражении, то должен появиться множитель. Он будет приводить эту ставку к той частоте начислений, которая предусмотрена эмитентом облигации.
Предположим, начисление происходит ежеквартально, то есть четыре раза в год. Тогда каждая ставка rn должна быть умножена на одну четвертую. Казалось бы, все просто, но не тут-то было. В зависимости от рынка и от эмитента существует понятие Day count convention. Оно говорит о том, что в качестве множителя степени нужно использовать текущее количество дней (например, в квартале или в месяце), прошедшее между купонными выплатами, деленное на 360 или 365.
В литературе можно встретить следующие выражения:
ACT/360
ACT/365
Кроме этого, встречается запись ACT/ACT. Таким образом, если начисление купонного дохода происходит ежемесячно и в текущем месяце 31 день, мы должны считать как 31/365(или 31/366 для високосного года). Также удобно использовать соглашение, когда независимо от месяца и от года множитель для вычисления выплат для дисконтирования купонов выбирается 30/360.
Еще одним рыночным соглашением является соглашение о цене облигации. Существует понятие так называемой «грязной» и «чистой» цены облигации. Чистая цена облигации – это цена облигации без накопленного купонного дохода.
Изобразим графически, как меняется стоимость облигации. Допустим, у нас есть облигация, и через определенные периоды времени должно происходить начисление купона по ней. Если мы не учитываем купонные начисления, то цена облигации меняется примерно так:
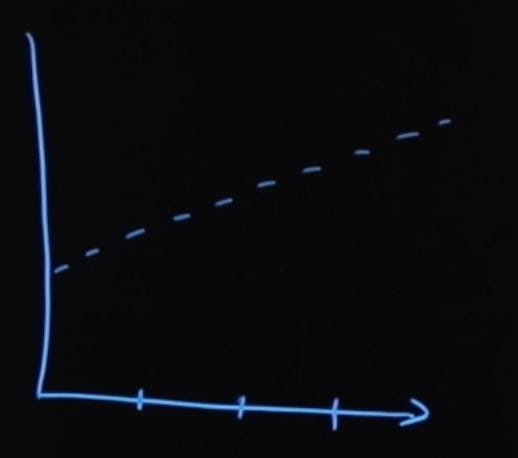
Однако из-за того, что есть купонный доход, который с каждым днем в периоде становится все больше и больше, этот купонный доход будет начисляться, выплачиваться и обнуляться в конце каждого периода начисления купона.
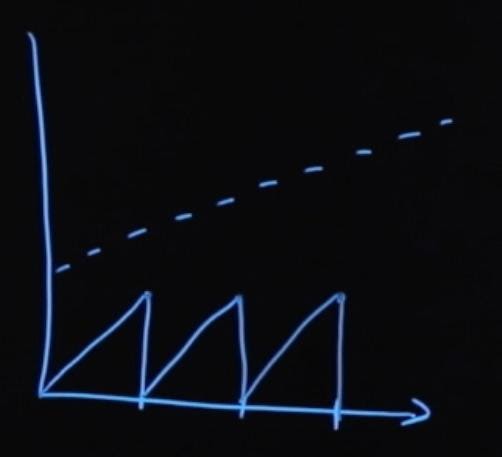
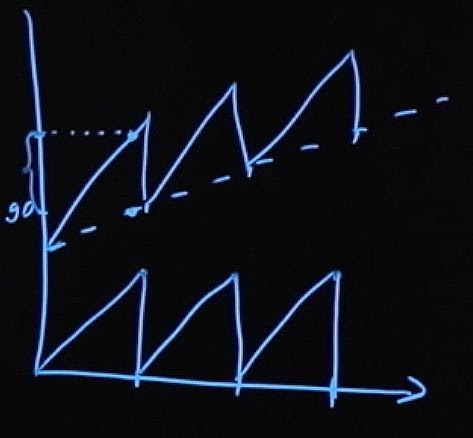
Если мы сложим эти два графика, то увидим, что цена облигации меняется примерно так:

Когда мы смотрим в какой-то информационный терминал, или кто-то предлагает нам облигацию по какой-то цене, она всегда предлагается нам по чистой цене (пунктирная линия). Происходит это потому, что это удобно – смотря на цену, мы лучше понимаем взаимосвязь цены с процентными ставками и можем не учитывать накопленный купонный доход. При этом, когда при покупке облигации происходит расчет по ней, всегда выплачивается грязная цена облигации (чистая цена, которая котировалась, плюс процентный доход, который на тот момент накопился).
Это, пожалуй, все основные моменты, которые следует знать, когда мы говорим о ценах на облигации и о том, как они котируются и рассчитываются.
Что влияет на цены облигаций? Как было сказано ранее, связь цены облигации и процентных ставок на рынке имеет обратно пропорциональную зависимость. Также на цены облигации влияет и время, оставшееся до погашения. Изобразим это схематически.
Допустим у нас было три облигации. Одна торговалась по номиналу, еще одна торговалась с какой-то премией, и третья облигация торговалась с дисконтом. Будем считать, что все три облигации имели одинаковый срок погашения – пять лет. Цена этих облигаций будет меняться в зависимости от времени до погашения:
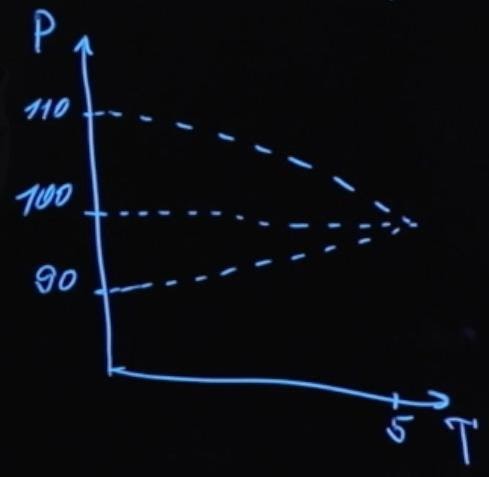
P – цена, а T – время, оставшееся до погашения. Облигации, которые продаются с премией, по мере приближения к моменту погашения падают в цене до номинального значения. Облигации которые продаются со скидкой, по мере приближения к моменту погашения растут в цене до номинального значения. Стоимость облигации, продаваемой по номиналу, не зависит от оставшегося времени до погашения.
Обратите внимание, что это касается только зависимости цены от времени до момента погашения. На стоимость облигации может влиять целый ряд иных факторов, например, изменение процентных ставок на рынке, которое оказывает свое отдельное влияние (при росте процентных ставок цена облигации уменьшается, при снижении процентных ставок цена облигации растет).
У нас есть облигация на три года. Купон, который выплачивается по этой облигации, равняется 5%. Доходность этой облигации равняется 4,5%. Доходность по-английски звучит как Yield to Maturity, и далее для удобства мы будем использовать английский акроним YMT.
3Y, С = 5%
YMT = 4,5%
Купон по облигации выплачивается раз в год. Выглядит это так: в течении года накапливается купонный доход и выплачивается в конце года. То же самое происходит во второй год. В третий год выплачивается купонный доход, и возвращается номинал облигации держателю.
Наша облигация выпущена 15 мая 2019 года, а 1 июня 2019 года мы решили ее кому-то продать. Какая должна быть цена? Давайте вспомним, что цена облигации равняется сумме дисконтированных купонных платежей плюс дисконтированный номинал нашей облигации.
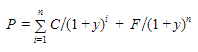
Отсюда мы получим следующее: до выплаты первого купона пройдет 349 дней. До выплаты второго купона — 714 дней. И последний купон вместе с номиналом облигации будет выплачен через 1079 дней.
Эти дни нам нужны для того, чтобы точно рассчитать купонные выплаты, используя соглашение о подсчете дней.
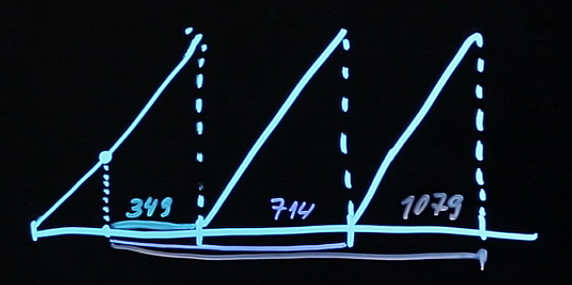
Будем использовать здесь соглашение о подсчете дней в следующем виде: ACT/365. Тогда цена облигации будет равна купону (5%), умноженному на номинал облигации, который равен 100, деленному на единицу плюс процентная ставка доходности, в степени 349/365 (это то количество дней, которое у нас остается с момента покупки до выплаты первого купона).
Аналогично следующий купон: пять, деленное на единицу плюс доходность, в степени 714/365 (это сколько осталось до выплаты второго купона). И купон плюс номинал облигации, который будет выплачен в конце третьего года, деленное на единицу плюс доходность, в степени 1079/365. Все это будет равняться 101,57.
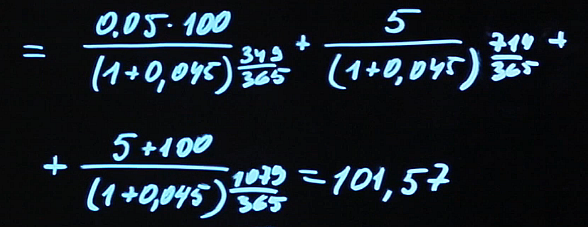
Что это за цена? Это грязная цена облигации. Потому как она включает в себя весь накопленный купонный доход при выплате в первый год. Но мы покупаем облигацию и выплачиваем при этом продавцу накопленный купонный доход за первые 17 дней. Чтобы вычислить чистую цену, нам необходимо посчитать накопленный купонный доход, который будет равняться купону (5 рублей), умноженному на 17/365 (это то, сколько держатель облигации получал доход), что в итоге будет равняться 0,23 руб.

Тогда мы можем посчитать, чему будет равна чистая цена облигации. Та самая, которую мы можем увидеть в информационном терминале.
PC = PD — HKD
PC (цена чистая — clean) равняется PD (цена грязная — dirty) минус накопленный купонный доход. Подставим значения, и у нас получится:
PC = 101,57 — 0,23 = 101,34
Легко увидеть, что мы получили бы совершенно другую цену, если бы соглашение о подсчете дней было бы другое. Вот почему важно учитывать соглашение о подсчете дней, действующее для конкретного инструмента на том рынке, на котором вы его покупаете.
Все статьи этой серии
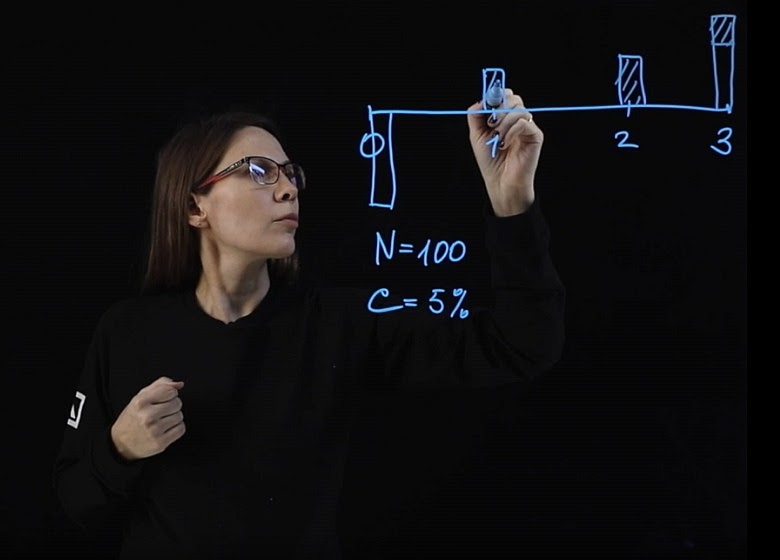
В основе этого поста – две мои лекции из курса Finmath for Fintech, записи которых можно найти тут: «Облигации» и «Рыночные соглашения».
#4. Облигации
Облигация – это финансовый инструмент, по которому выплачивается на заранее оговоренную сумму в заранее оговоренные периоды времени какой-то процентный доход.
Рассмотрим, как будет выглядеть структура платежей по облигациям. Предположим, у нас есть трехлетняя облигация. При покупке облигации покупатель должен сделать платеж в размере номинала облигации. Пусть в нашем примере номинал облигации N составит 100 рублей. Регулярно будут производиться выплаты купонов по облигации. Купонный платеж измеряется в процентах. Предположим, что он равен пяти процентам (С=5%). В конце срока действия облигации (в момент погашения) держатель получает назад номинал и последний купонный платеж.
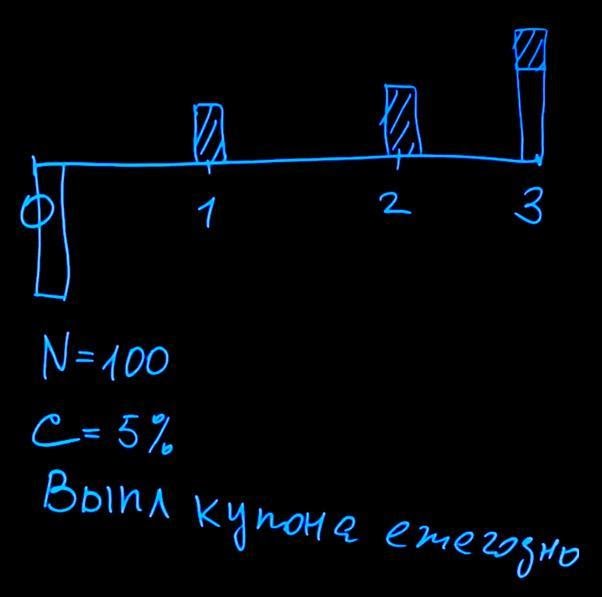
Выплаты купона, как показано на рисунке, происходят ежегодно. В принципе, эмитент облигации может назначать любую частоту выплат, например, ежеквартально или раз в полгода.
Бескупонные облигации
Есть также вид облигации, по которой купон не платится вообще – бескупонная облигация (Zero-coupon bond). Такая облигация покупается со скидкой от номинала (с дисконтом). Номинал этой облигации выплачивается при погашении, а в начале покупателем платится некоторая сумма, которая меньше номинала. Прибылью по такой облигации будет разница между ценой покупки облигации и номиналом этой облигации. Предположим, ее номинал сто рублей N=100, и дисконт по этой облигации составляет пять процентов d=5%, погашение через год. Согласно формуле дисконтирования, текущая стоимость облигации будет равна номиналу, дисконтированному по этой ставке в пять процентов.
PV=N/(1+d)=100/1,05=95,24 руб.
Это пример расчета справедливой цены самой простой облигации. Следует отметить, что если бескупонная облигация со сроком действия на год выпущена не сегодня, а, скажем, полгода назад, и мы хотим ее купить, цена облигации будет выше. Потому что за счет того, что уже прошло полгода, мы будем дисконтировать по меньшей процентной ставке, и, соответственно, облигация будет стоить дороже.
Срок действия по облигациям называется maturity. В момент maturity (выплаты номинала) стоимость облигации будет равняться ее номиналу, в нашем примере – ста рублям.
Цена купонной облигации
Давайте попробуем посчитать цену купонной облигации. Способ расчета будет очень похож на расчет бескупонной облигации. Вспомним, о чем говорилось ранее про дисконтирование: для того чтобы узнать стоимость облигации, нам нужно каждый купонный платеж привести к текущему моменту времени и просуммировать выплаты. Запишем это.
PV=C/(1+r1) + C/(1+r2)2 + (C+F)/(1+r3)3
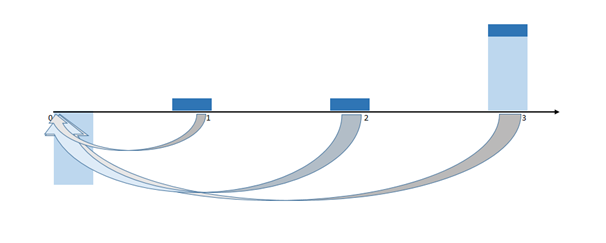
Цена облигации будет состоять из трех частей: первый купон, дисконтированный по процентной ставке на один год, плюс второй купон, дисконтированный по процентной ставке на два года, и плюс последний купон, плюс номинал, или face value облигации, дисконтированный по процентной ставке на три года.
Рассмотрим, как будет выглядеть формула расчета цены облигации, если количество периодов начисления процентов не три, а больше. В общем виде мы получим сумму дисконтированных купонных доходов при значении n от единицы до T (количество периодов) плюс последняя выплата номинала нашей облигации, дисконтированная по ставке, которая действует на период времени T.

Как видите, не обязательно запоминать формулу расчета, ее легко можно вывести из общих соображений относительно того, какая структура платежей по данному продукту.
Доходность к погашению
Одним из важных показателей облигации как инструмента является понятие доходности к погашению (Yield to Maturity). Это единая процентная ставка доходности облигации, которую получит держатель в том случае, если облигацию он держит до самого погашения, то есть ждет выплаты всех купонов и номинала в конце (а не продает ее в середине). Как определить эту доходность?
Для бескупонной облигации все достаточно просто – та ставка дисконта, с которой мы покупаем нашу облигацию, и будет являться доходностью к погашению. В нашем примере при покупке с дисконтом пять процентов доходность по облигации составит пять процентов. А как быть с купонной облигацией? Дело в том, что каждый купон дисконтируется по своей собственной ставке. Пока мы опустим, каким образом рассчитываются эти ставки (они рассчитываются исходя из текущих цен инструментов). Чтобы узнать доходность облигации к погашению, нужно, зная текущую цену облигации, вместо процентных ставок, по которым мы дисконтируем, подставить единую ставку. Решив уравнение n-ой степени, можно определить размер этой самой доходности.
Стоит также отметить, что важным фактором, влияющим на цену облигации, являются процентные ставки. Если мы держим облигацию до погашения, то на нас изменение процентных ставок никак не влияет, потому что нам не важно, как меняется текущая цена облигации, мы ее держим ради купонного дохода. Если же мы хотим облигацию продать в течение срока ее действия, то важно понимать, что изменение процентных ставок приводит к изменению цены облигации.
Так, если мы сегодня купили облигацию за сто рублей, то при росте процентных ставок цена облигации изменится, облигация будет стоить дешевле. Изменение процентных ставок и цены облигации обратны – если процентные ставки растут, цена облигации снижается, и наоборот (если процентные ставки снижаются, то цена облигации растет).
Немного истории
Как вы думаете, когда впервые появилась облигация? Честно говоря, когда я впервые узнала об этом финансовом инструменте, я думала, что это что-то, что было изобретено в XIX веке для торговли на американских биржах. Оказывается, первые облигации были изобретены шесть веков назад. Одним из первых эмитентов была Ост-Индская компания, которая занималась тем, что перевозила специи, и ей было даже совершено несколько крупных географических открытий. Это была крупнейшая компания своего времени, ее капитализация в пересчете на нынешние деньги составляла более семи триллионов долларов. Это больше, чем капитализация Apple и Google. Неудивительно, что такая огромная компания активно привлекала заемные средства на свои масштабные экспедиции. На изображении ниже вы можете видеть, как выглядели облигации этой компании от 1622 года.

Уже в девятнадцатом веке облигации использовались массово. Так, например, облигации выпускались Российской империей.
Примерно в то же самое время в обиходе появилось выражение «стричь купоны». Когда мы сегодня произносим эту фразу, мы подразумеваем, что какой-то человек получает фиксированный доход, не прикладывая к этому усилий.
Все дело в том, что в XIX веке облигации выпускались на листе бумаги, который представлял из себя саму ценную бумагу и часть, на которой располагались купоны.

В каждом купоне указывался размер выплаты по этому купону и время, когда можно прийти и получить выплату. Для того, чтобы купон оплатили, необходимо было вырезать его из листа бумаги и предъявить. Владельцы облигаций стригли купоны и получали доход со своих вложений.
Кто может выпустить облигации? Ограничений нет, и эмитентом облигации может быть кто угодно. Облигации выпускают государства, городские муниципалитеты, коммерческие компании. Даже мелкие компании могут выпустить свои облигации. В зависимости от эмитента облигации будут иметь разное кредитное качество. Эту тему мы рассмотрим чуть ниже.
#5. Рыночные соглашения
На рынке существуют определенные соглашения, которыми пользуются все его участники. При заключении сделок эти соглашения отдельно даже не оговариваются — это, своего рода, общее понимание. Касается оно и цен на облигации.
Цена облигации – это по сути процент от номинала облигации. Допустим, номинал облигации — тысяча или десять тысяч рублей. Если мы попросим продавца облигации назвать ее цену, он назовет цифры, например, 98, 100 или 105. Эти числа определяются процентами от номинала облигации, то есть цена облигации – это процент от ее номинала. Таким образом, если нам называют цену меньше ста, это означает, что облигация торгуется со скидкой (с дисконтом). Если облигацию нам продают за сто – означает, что ее продают по номиналу (Par Value). Ну, а если цена на облигацию оказывается выше ста, значит, она торгуется с премией.
Почему облигация может продаваться с дисконтом либо с премией? Если процентная ставка по купону выше существующих рыночных процентных ставок, то такая облигация скорее всего будет продаваться с премией, потому что это возможность для покупателя облигации заработать больший купонный доход, чем по другим существующим на рынках инструментам. Поэтому данная возможность закладывается в цену облигации, при приобретении покупатель платит больше, чем номинал.
Аналогично с дисконтированием. Если у нас получается, что процентная ставка по купону ниже, чем существующие на рынке процентные ставки, то покупателю будет предложена скидка от номинала облигации для того, чтобы он эту облигацию купил.
Соглашение о подсчете дней
Еще одним важным рыночным соглашением на рынке облигаций является соглашение о подсчете дней (Day count convention). Вспомним формулу расчета цены облигации и обсудим, что же такое Day count convention.
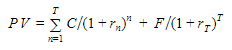
Цена облигации равняется сумме дисконтированных купонных платежей плюс дисконтированный номинал облигации. В частном случае, если у нас происходит начисление купонного дохода чаще, чем раз в год, то так как ставка rn выражена в годовом выражении, то должен появиться множитель. Он будет приводить эту ставку к той частоте начислений, которая предусмотрена эмитентом облигации.
Предположим, начисление происходит ежеквартально, то есть четыре раза в год. Тогда каждая ставка rn должна быть умножена на одну четвертую. Казалось бы, все просто, но не тут-то было. В зависимости от рынка и от эмитента существует понятие Day count convention. Оно говорит о том, что в качестве множителя степени нужно использовать текущее количество дней (например, в квартале или в месяце), прошедшее между купонными выплатами, деленное на 360 или 365.
В литературе можно встретить следующие выражения:
ACT/360
ACT/365
Кроме этого, встречается запись ACT/ACT. Таким образом, если начисление купонного дохода происходит ежемесячно и в текущем месяце 31 день, мы должны считать как 31/365(или 31/366 для високосного года). Также удобно использовать соглашение, когда независимо от месяца и от года множитель для вычисления выплат для дисконтирования купонов выбирается 30/360.
Грязная и чистая цены
Еще одним рыночным соглашением является соглашение о цене облигации. Существует понятие так называемой «грязной» и «чистой» цены облигации. Чистая цена облигации – это цена облигации без накопленного купонного дохода.
Изобразим графически, как меняется стоимость облигации. Допустим, у нас есть облигация, и через определенные периоды времени должно происходить начисление купона по ней. Если мы не учитываем купонные начисления, то цена облигации меняется примерно так:

Однако из-за того, что есть купонный доход, который с каждым днем в периоде становится все больше и больше, этот купонный доход будет начисляться, выплачиваться и обнуляться в конце каждого периода начисления купона.

Если мы сложим эти два графика, то увидим, что цена облигации меняется примерно так:

Когда мы смотрим в какой-то информационный терминал, или кто-то предлагает нам облигацию по какой-то цене, она всегда предлагается нам по чистой цене (пунктирная линия). Происходит это потому, что это удобно – смотря на цену, мы лучше понимаем взаимосвязь цены с процентными ставками и можем не учитывать накопленный купонный доход. При этом, когда при покупке облигации происходит расчет по ней, всегда выплачивается грязная цена облигации (чистая цена, которая котировалась, плюс процентный доход, который на тот момент накопился).
Поэтому, покупая облигацию по чистой цене 90, вы должны также иметь средства, чтобы доплатить продавцу надбавку в виде купонного дохода по этой облигации.

Это, пожалуй, все основные моменты, которые следует знать, когда мы говорим о ценах на облигации и о том, как они котируются и рассчитываются.
Что влияет на цены облигаций? Как было сказано ранее, связь цены облигации и процентных ставок на рынке имеет обратно пропорциональную зависимость. Также на цены облигации влияет и время, оставшееся до погашения. Изобразим это схематически.
Допустим у нас было три облигации. Одна торговалась по номиналу, еще одна торговалась с какой-то премией, и третья облигация торговалась с дисконтом. Будем считать, что все три облигации имели одинаковый срок погашения – пять лет. Цена этих облигаций будет меняться в зависимости от времени до погашения:
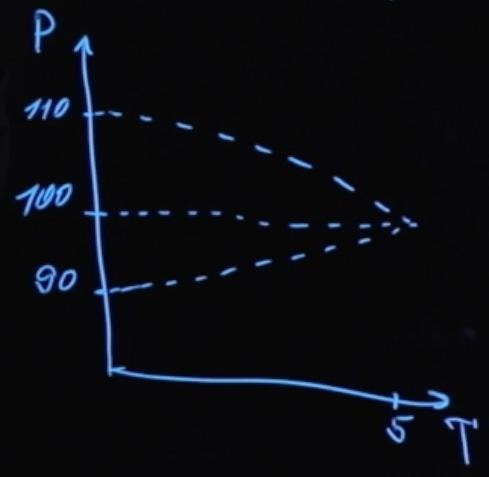
P – цена, а T – время, оставшееся до погашения. Облигации, которые продаются с премией, по мере приближения к моменту погашения падают в цене до номинального значения. Облигации которые продаются со скидкой, по мере приближения к моменту погашения растут в цене до номинального значения. Стоимость облигации, продаваемой по номиналу, не зависит от оставшегося времени до погашения.
Обратите внимание, что это касается только зависимости цены от времени до момента погашения. На стоимость облигации может влиять целый ряд иных факторов, например, изменение процентных ставок на рынке, которое оказывает свое отдельное влияние (при росте процентных ставок цена облигации уменьшается, при снижении процентных ставок цена облигации растет).
Пример с использованием грязной и чистой цен и соглашением о подсчете дней
У нас есть облигация на три года. Купон, который выплачивается по этой облигации, равняется 5%. Доходность этой облигации равняется 4,5%. Доходность по-английски звучит как Yield to Maturity, и далее для удобства мы будем использовать английский акроним YMT.
3Y, С = 5%
YMT = 4,5%
Купон по облигации выплачивается раз в год. Выглядит это так: в течении года накапливается купонный доход и выплачивается в конце года. То же самое происходит во второй год. В третий год выплачивается купонный доход, и возвращается номинал облигации держателю.
Наша облигация выпущена 15 мая 2019 года, а 1 июня 2019 года мы решили ее кому-то продать. Какая должна быть цена? Давайте вспомним, что цена облигации равняется сумме дисконтированных купонных платежей плюс дисконтированный номинал нашей облигации.

Отсюда мы получим следующее: до выплаты первого купона пройдет 349 дней. До выплаты второго купона — 714 дней. И последний купон вместе с номиналом облигации будет выплачен через 1079 дней.
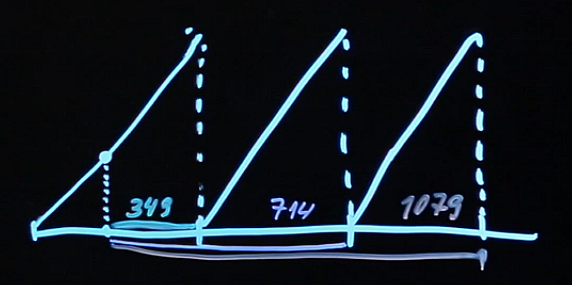
Эти дни нам нужны для того, чтобы точно рассчитать купонные выплаты, используя соглашение о подсчете дней.
Будем использовать здесь соглашение о подсчете дней в следующем виде: ACT/365. Тогда цена облигации будет равна купону (5%), умноженному на номинал облигации, который равен 100, деленному на единицу плюс процентная ставка доходности, в степени 349/365 (это то количество дней, которое у нас остается с момента покупки до выплаты первого купона).
Аналогично следующий купон: пять, деленное на единицу плюс доходность, в степени 714/365 (это сколько осталось до выплаты второго купона). И купон плюс номинал облигации, который будет выплачен в конце третьего года, деленное на единицу плюс доходность, в степени 1079/365. Все это будет равняться 101,57.

Что это за цена? Это грязная цена облигации. Потому как она включает в себя весь накопленный купонный доход при выплате в первый год. Но мы покупаем облигацию и выплачиваем при этом продавцу накопленный купонный доход за первые 17 дней. Чтобы вычислить чистую цену, нам необходимо посчитать накопленный купонный доход, который будет равняться купону (5 рублей), умноженному на 17/365 (это то, сколько держатель облигации получал доход), что в итоге будет равняться 0,23 руб.

Тогда мы можем посчитать, чему будет равна чистая цена облигации. Та самая, которую мы можем увидеть в информационном терминале.
PC = PD — HKD
PC (цена чистая — clean) равняется PD (цена грязная — dirty) минус накопленный купонный доход. Подставим значения, и у нас получится:
PC = 101,57 — 0,23 = 101,34
Легко увидеть, что мы получили бы совершенно другую цену, если бы соглашение о подсчете дней было бы другое. Вот почему важно учитывать соглашение о подсчете дней, действующее для конкретного инструмента на том рынке, на котором вы его покупаете.
Все статьи этой серии
- Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч. 1
- Облигации: купонные и бескупонные, расчет доходности. Ликбез для гика, ч. 2
- Облигации: оценка рисков и примеры использования. Ликбез для гика, ч. 3
- Как банки берут друг у друга в долг. Плавающие ставки, процентные свопы. Ликбез для гика, ч. 4
- Построение кривой дисконтирования. Ликбез для гика, ч. 5
- Что такое опционы и кому это нужно. Ликбез для гика, ч. 6
- Опционы: пут-колл парити, броуновское движение. Ликбез для гика, ч. 7