SmartEngines 15 мая 2023 в 14:21

Как быстро вычисляются логарифм и экспонента в компьютере?

7 мин

Блог компании Smart EnginesМатематика*Алгоритмы*

Сегодняшняя статья посвящена методам быстрого приближенного вычисления двоичного логарифма и экспоненты/степеней двойки. Не все задумывались, как именно реализовано вычисление нелинейных математических функций в компьютере, который вообще-то умеет складывать и умножать, но не вычислять синусы или гиперболические тангенсы. Из ~~школьных~~ институтских времен вспоминаются ряды Тейлора, приближающие функцию полиномом в окрестности заданной точки, или интерполяционные полиномы Лагранжа, но как добиться действительно высокой точности приближения? А можно ли эти имплементации ускорить? Постараемся сегодня приоткрыть завесу тайны.

Для начала нужно вспомнить, как устроен формат вещественных чисел.

1. Вещественная арифметика

Для представления вещественных чисел в компьютере наиболее широко употребляются форматы данных, определенные стандартом арифметики с плавающей точкой IEEE 754. Этот стандарт был разработан Институтом инженеров электротехники и электроники (IEEE) в 1985 году, а затем обновлен в 2008 и 2019 годах. Его использование обеспечивает одинаковые результаты вычислений для программных, аппаратных или комбинированных реализаций вещественной арифметики, а также предоставляет единый формат ошибок, не привязанный к конкретной реализации.

Вещественные числа в двоичных форматах из стандарта IEEE 754 состоят из 3 упорядоченных полей:

1-битный знак числа S,
w-битовая сдвинутая экспонента или порядок
(t = p-1)-битовая мантисса $T=d_1 d_2 … d_{p-1},$ где $d_i \in \{0, 1\}$ – двоичные разряды мантиссы, причем лидирующий разряд неявным образом закодирован в экспоненте.
Вместе они составляют (w+p)-битовое число, как показано на Рис. 1.
Рис. 1. 32-битное вещественное число.

Вещественное число может принимать следующие значения:

NaN – не-числовое значение. При этом и $T \neq 0$ , причем значение бита определяет дальнейшие действия: продолжение вычислений или сигнал об ошибке.
Бесконечность. $v=(-1)^S \cdot (+\infty)$ , когда и .
Нормализованное число. $v=(-1)^S \cdot 2^{E-bias} \cdot (1+2^{1-p}T)$ , когда $1 \leq E \leq 2^w - 2$ .
Денормализованное число. $v=(-1)^S \cdot 2^{emin} \cdot (0+2^{1-p}T)$ , где – минимальное значение . Задается с помощью и $T \neq 0$ .
Нулевое значение. Если и , тогда $v=(-1)^S \cdot (+0)$ .

Отметим, что денормализованные числа не превышают по абсолютному значению минимальное нормализованное число.

Как вы знаете, мы в Smart Engines занимаемся системами распознавания и обычно имеем дело с изображениями. В задачах обработки изображений или машинного обучения чаще всего используются 32-битные вещественные числа, поэтому дальнейшие примеры приведены для него. Это привычный С++ тип данных float, который называется binary32 согласно IEEE 754. Он использует следующий набор параметров: . Более того, мы дополнительно упростим себе задачу, заметив, что денормализованные числа нам нужны крайне редко и мы ничего не потеряем, если будем считать их нулевыми. Это можно сделать, изменив флаги в управляющем регистре вещественной арифметики на конкретной платформе. Например, на x86_64 с вещественной арифметикой в SSE-режиме это регистр MXCSR и флаги DAZ (denormals-are-zero) and FTZ (flush-to-zero), которые можно установить с помощью интринсиков SSE.

2. Вычисление двоичного логарифма

2.1. Точное вычисление

В качестве примера мы рассмотрим точную реализацию двоичного логарифма для типа данных float из Cephes mathematical library [1], разработанной в 80-е Стивеном Л. Мошиером (Stephen L. Moshier) и позднее ставшей частью многих библиотек и пакетов для научных вычислений, например, SciPy.

И вот что там можно увидеть:

 /* The argument is separated into its exponent and fractional
 * parts.  If the exponent is between -1 and +1, the base e
 * logarithm of the fraction is approximated by
 *
 *     log(1+x) = x - 0.5 x**2 + x**3 P(x)/Q(x).
 *
 * Otherwise, setting  z = 2(x-1)/(x+1),
 * 
 *     log(x) = z + z**3 P(z)/Q(z).
 *
 *
 *
 * ACCURACY:
 *
 *                      Relative error:
 * arithmetic   domain     # trials      peak         rms
 *    IEEE      exp(+-88)   100000      1.1e-7      2.4e-8
 *    IEEE      0.5, 2.0    100000      1.1e-7      3.0e-8
 */
/*
Cephes Math Library Release 2.2:  June, 1992
Copyright 1984, 1992 by Stephen L. Moshier
Direct inquiries to 30 Frost Street, Cambridge, MA 02140
*/

То есть, используется две аппроксимации для диапазона аргумента возле нуля и остальной числовой прямой, каждая из которых представляет собой аппроксимацию Паде – рациональную функцию, представляющую собой частное двух полиномов. В данном случае полином Q(x) единичный, а P(x) содержит 9 коэффициентов.

2.2. Полиномиальное приближение

Что делают математики, когда хочется вычислить что-то сложное побыстрее? Разумеется, они пытаются приблизить это что-то более простой структурой. Поэтому мы рассмотрели относительно простую полиномиальную аппроксимацию двоичного логарифма.

Рассмотрим вещественное число :

$x = 2^e \cdot (1 + 2^{-23} d_1d_2\dots d_{23}),$

где .

Для него

$\log_2 x = e + \log_2 (1 + 2^{-23} d_1d_2\dots d_{23}) = e + \log_2(1+y),$

Это означает, что необходимо приблизить $\log_2 (1 + y)$ для $y \in [0, 1)$ .

Полиномиальная аппроксимация 5-го порядка выглядит следующим образом:

$f(y) = \log_2 (1 + y) \rightarrow \tilde{f}(y) = \sum_{i=0}^5 C_i y^i$

Для определения коэффициентов составим систему линейных уравнений: в трех точках 0, 0.5, 1 значения должны быть равны значениям $\tilde{f}(y)$ , а значения – значениям $\tilde{f}'(y)$ . В результате ее численного решения были получены значения $C=\{0, 1.44269504, -0.71249131, 0.42046732, -0.1955884, 0.04491735\}.$ Максимальная ошибка аппроксимации составила около $7 \cdot 10^{-5}$ на промежуткеМы хотели использовать эту аппроксимацию в биполярных морфологических нейронных сетях, поэтому целевой диапазон был именно таким.

Эта аппроксимация использует всего 5 умножений и 6 сложений при вычислении с помощью схемы Горнера (включая вычитание, чтобы получить ), если считать, что доступ к битам числа для получения значений экспоненты и мантиссы не требует дополнительного времени.

Хорошо? В принципе, да. Но можно ли еще быстрее? Оказывается, что да.

2.3. Аппроксимация Митчелла

Пожалуй самой вычислительно-эффективной аппроксимацией двоичного логарифма является аппроксимация, предложенная Дж. Митчеллом [2].

Он предложил использовать первый член ряда Маклорена чтобы аппроксимировать $\log_2(1+y)$ :

$\log_2\left(1+y\right)\approx y.$

Тогда

$\log_2 x =e + y$

Таким образом, вычислительная сложность этой аппроксимации составляет всего две операции сложения/вычитания (включая вычитание, чтобы получить ).

Эта аппроксимация будет кусочно-линейной, причем концы каждого отрезка расположены в точках, равных степеням двойки. Максимальное по абсолютной величине отклонение от точной функции двоичного логарифма можно определить аналитическим путем для каждого промежутка, например, на промежуткеоно составляет .

На Рис. 2 показано сравнение различных реализаций двоичного логарифма. Можно видеть, что наша тривиальная полиномиальная аппроксимация обеспечивает хорошее приближение только на целевом интервале, а при больших значениях аргумента значительно отклоняется от логарифма. При этом с качественной точки зрения аппроксимация Митчелла ведёт себя гораздо лучше, хотя и имеет большую погрешность на .

Рис. 2 Различные реализации двоичного логарифма.

3. Вычисление

На самом деле, экспонента и возведение в степень вычисляются практически одинаково:

$e^{x} = 2^{x /\ln 2}$

Стандарт IEEE 754 оперирует двоичным представлением числа, поэтому удобнее всего перейти к возведению в степень именно двойки.

3.1. Точное вычисление

Покажем, какая аппроксимация используется в Cephes:

/* Returns 2 raised to the x power.
 *
 * Range reduction is accomplished by separating the argument
 * into an integer k and fraction f such that
 *     x    k  f
 *    2  = 2  2.
 *
 * A polynomial approximates 2**x in the basic range [-0.5, 0.5].
 *
 *
 * ACCURACY:
 *
 *                      Relative error:
 * arithmetic   domain     # trials      peak         rms
 *    IEEE     -127,+127    100000      1.7e-7      2.8e-8
 */

То есть, сначала выделяется целая часть . Так как нормализованное вещественное число записывается следующим образом:

$y = 2^{e} \cdot (1 + 2^{-23} d_1d_2\dots d_{23}),$

для вычисления , где – целое, необходимо просто записать в поле экспоненты, то есть:

$i=2^{23}\left(x+bias\right),$

где – непосредственное представление вещественного числа. Напомним, что – это константа, определяемая типом данных и равная 127 для binary32. Для приближения дробной части в данном случае использовался полином 5 степени.

Кроме того, современные процессоры x86_64 могут включать в себя специальные инструкции для быстрого вычисления экспоненты, как, например, процессоры Intel [3]. При этом используется таблица предподсчитанных значений и полиномиальная аппроксимация второго порядка, а значит ее сложность составляет 3 операции сложения и 3 операции умножения, не считая операции доступа по индексу таблицы. Относительная ошибка такой аппроксимации меньше $2^{-23}$ , то есть она дает точные результаты при вычислении в типе binary32.

3.2. Аппоксимация Шраудольфа

В 1999 году Н. Шраудольф предложил крайне эффективную для вычисления аппроксимацию экспоненциальной функции [3], основанную на структуре двоичных форматов IEEE 754 для представления вещественных чисел. В его работе рассмотрены данные типа binary64 или double, однако предложенный подход можно легко распространить на binary32, что мы сейчас и сделаем.

Нормализованное вещественное число записывается следующим образом:

$y = 2^{e} \cdot (1 + 2^{-23} d_1d_2\dots d_{23}),$

Как возводить 2 в целую степень, мы уже знаем. Оказывается, подобное можно провернуть и для вещественного . Для этого умножим его на $2^{23}$ , преобразуем к целому, а затем прибавим $2^{23} \cdot bias$ . При этом младшие разряды такого числа будут ненулевыми и осуществят линейную интерполяцию между соседними целыми числами, для которых результат окажется точным (разумеется, пока не произошло переполнение). И последний штрих: для более точного в среднем приближения можно добавить поправочный коэффициент.

В результате аппроксимация Шраудольфа имеет вид:

$i=int(ax)+\left(b-c\right),$

где – непосредственное представление вещественного числа, $a = 2^{23},~b = 127 \cdot 2^{23},$ а – поправочный коэффициент, взятый равным 486411.

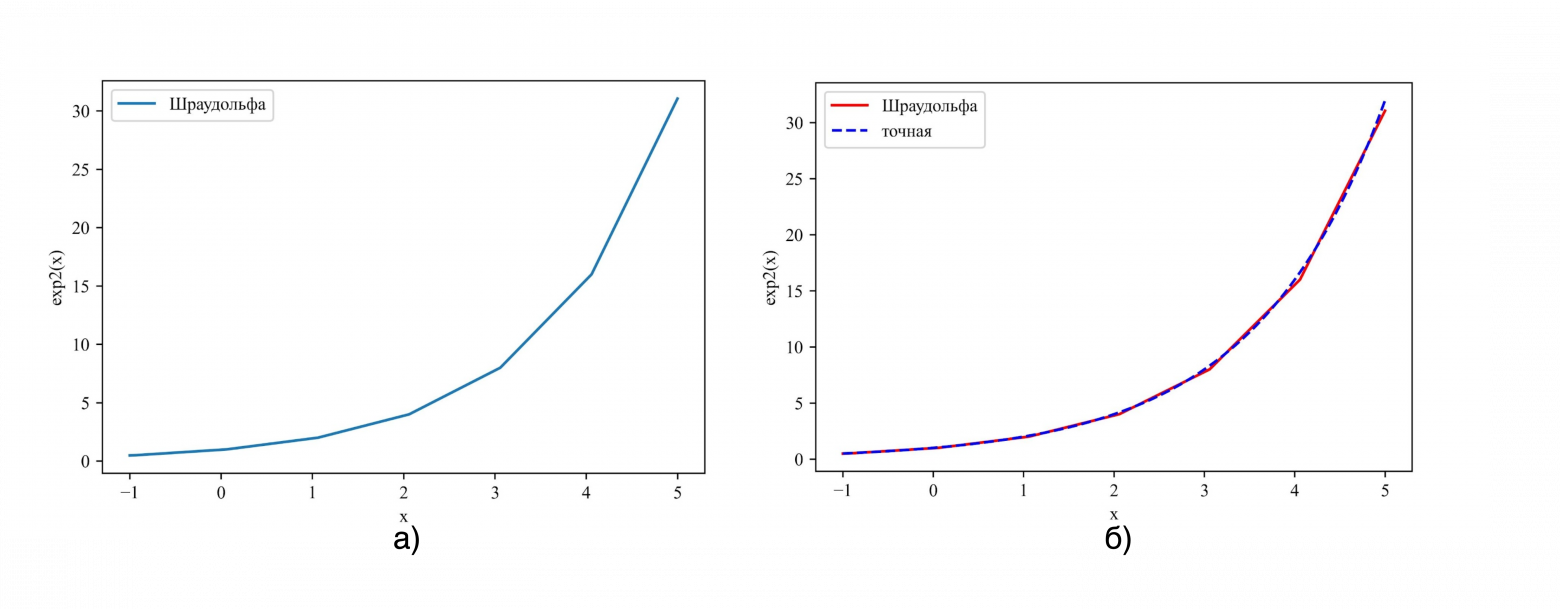
Эта аппроксимация использует одно целочисленное сложение, одно вещественное умножение и одно преобразование типа вещественного типа в целое число. Максимальное абсолютное отклонение от точной экспоненциальной функции на полуинтервале было определено численно и составило 0.05798 (см. Рис. 3).

Рис. 3. Различные реализации операции двоичного потенцирования: а) смотрите, она правда кусочно-линейная, б) сравнение с точной реализацией.

Экспериментальные результаты

В Таблице 1 приведены оценки точности каждой реализации и экспериментально измеренное время работы для 32-битных вещественных чисел (усредненное время на 1 операцию).

Функция	Точность		Время, нс
Устройство		Intel Core i7-9750H	AMD Ryzen Threadripper 2990WX	Odroid N2
std::log2f	точная / $\sim 10^{-7}$	4.6	9.6	14
Полиномиальная аппроксимация	$7 \cdot 10^{-5}$ на [1, 2)	2.4	0.7	5.3
Аппроксимация Митчелла	0.08639 на [1, 2)	1.1	0.5	1.7
std::exp2f	точная / $\sim 10^{-7}$	2.3	3.4	6.7
Аппроксимация Шраудольфа	0.05798 на [0, 1)	0.6	0.5	0.8

Можно видеть, что рассмотренные аппроксимации правда позволяют ускорить вычисления в несколько раз. Кроме того, аппроксимации Митчелла и Шраудольфа легко дополнительно векторизовать с помощью SIMD (наши замеры без векторизации). При этом отметим, что битовые операции для доступа к мантиссе и порядку в случае аппроксимации Митчелла оказались вовсе не бесплатными и аппроксимация Шраудольфа работает немного быстрее.

Теперь попробуем ответить на вопрос, который мог возникнуть у дочитавших до этого места: а есть ли практический смысл пользоваться аппроксимациями, ведь и время вычисления точных функций невелико? Действительно, рутинно оптимизировать нелинейные функции не нужно, поэтому данная статья носит в большей степени образовательный характер. Однако случаи, когда это становится нужно, все-таки существуют:

Когда программа, использующая эти функции, планируется к реализации в виде железки. Там доступ к битовому представлению числа становится бесплатным, а аппроксимация значительно экономит число транзисторов.
Когда при анализе признаков, найденных нейронной сетью, хочется посчитать от них значение softmax'а и сделать это не один раз, а много.
Это те случаи, с которыми сталкивались мы, но наверняка есть еще. А приходилось ли вам оптимизировать вычисление нелинейных функций?

Список литературы

[1] http://www.sai.msu.su/sal/B/0/CEPHES.html

[2] Mitchell J.N. Computer multiplication and division using binary logarithms. IRE Transactions on Electronic Computers. 1962 Aug(4):512-7.

[3] Schraudolph N. N. A fast, compact approximation of the exponential function. Neural Computation. 1999 May 15;11(4):853-62.

Теги:

Хабы: