В статье предложен новый весьма необычный способ определения экспоненты и на основе этого определения выведены её основные свойства.
Каждому положительному числу поставим в соответствие множество , где и .
Будем писать , если верхняя граница множества . Аналогично, будем писать , если — нижняя граница множества .
Проведём рассуждение по индукции.
Для утверждение очевидно: .
Пусть для .
Тогда
.
Лемма 2 доказана.
В дальнейшем мы покажем, что каждое множество ограничено. Из леммы 2 следует, что
(1)
Каждому положительному числу поставим в соответствие множество , где и .
Лемма 1. Из следует, что для каждого элемента найдётся элемент такой, что .
Будем писать , если верхняя граница множества . Аналогично, будем писать , если — нижняя граница множества .
Лемма 2. Если , то .
Доказательство
Проведём рассуждение по индукции.
Для утверждение очевидно: .
Пусть для .
Тогда
.
Лемма 2 доказана.
В дальнейшем мы покажем, что каждое множество ограничено. Из леммы 2 следует, что
(1)
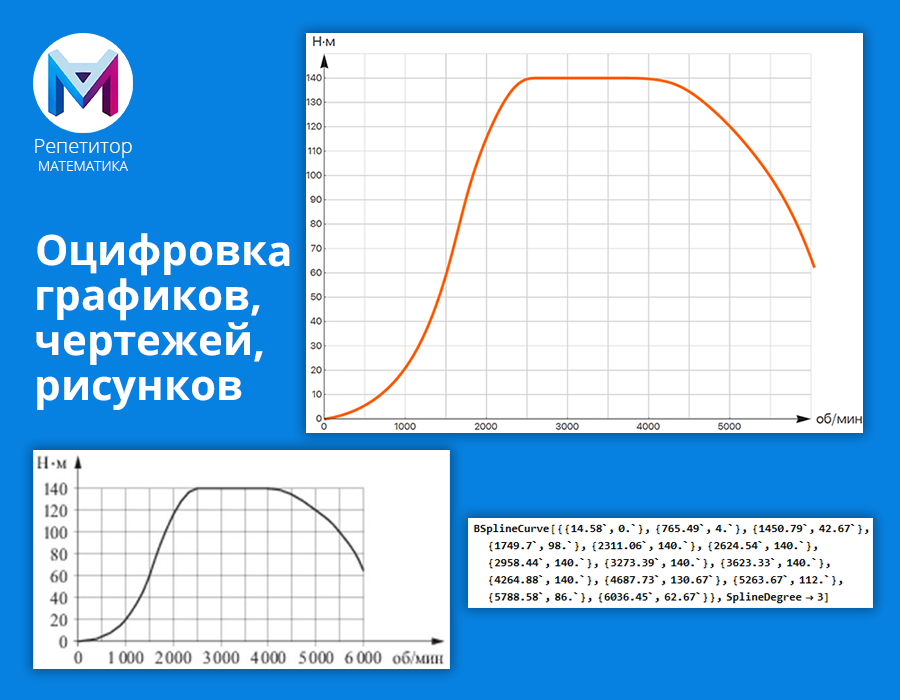


 Привет тебе, хабр! Меня зовут Максим и я работаю в отделе QA компании
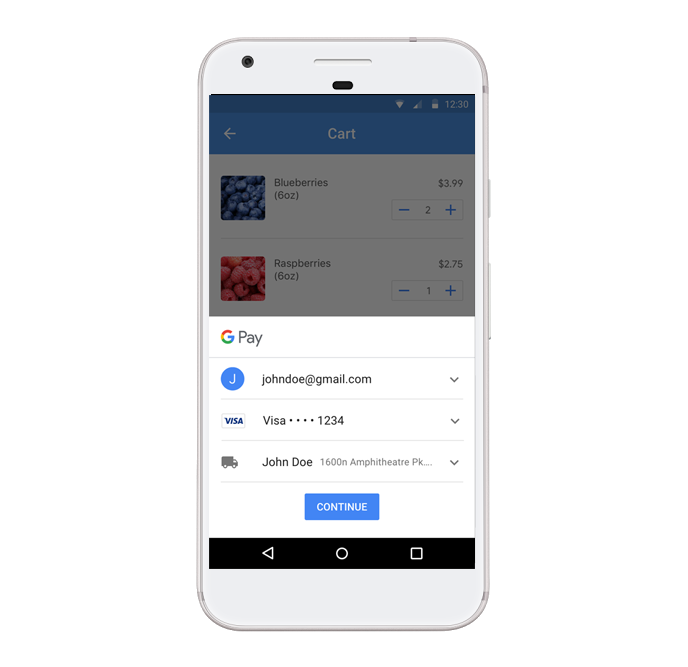
Привет тебе, хабр! Меня зовут Максим и я работаю в отделе QA компании  Меня зовут Оксана и я Android-разработчик в небольшой, но очень классной команде
Меня зовут Оксана и я Android-разработчик в небольшой, но очень классной команде