Странные аттракторы — это области, которые часто возникают в различных физических системах. Можно сказать, что это область притяжения, к которой стремятся траектории из некоторой окрестности. В отличие от каких-нибудь предельных циклов или от точки равновесия в затухающих колебаниях, они не периодичны. В таких системах проявляется эффект бабочки: минимальные отклонения исходных положений экспоненциально растут со временем.
Некоторые аттракторы завораживают своей красотой даже на статических картинках. Мы захотели сделать приложение, которое сможет визуализировать большинство аттракторов в динамике, в 3D и без лагов.
Мы — Венедиктов Роман, Носивской Владислав и Карнаухов Кирилл — студенты второго курса бакалаврской программы «Прикладная математика и информатика» в НИУ ВШЭ — Санкт-Петербург. Программированием увлекаемся со школьных времен. Все трое занимались олимпиадным программированием и проходили в разные годы на заключительный этап Всероссийской олимпиады школьников по информатике, но опыта промышленного программирования раньше не имели, и для нас это первый большой командный проект. Мы защищали его в качестве курсовой работы по С++.
Есть много способов задать динамическую систему со странным аттрактором, но чаще всего встречается система из трех дифференциальных уравнений первого порядка. Мы начали с нее.
Перед тем, как что-то визуализировать, нужно промоделировать сам процесс и найти траектории точек. Точные методы моделирования достаточно трудоемкие, а нам хотелось бы делать это максимально быстро.
При реализации моделирования мы решили использовать метапрограммирование, отказавшись от std::function и других подобных механик. Они могли дать упрощение в архитектуре и написании кода, но сильно уменьшили бы производительность, а этого нам не хотелось.
Для моделирования исходно был использован простейший метод Рунге — Кутты 4-го порядка точности с постоянным шагом. Пока мы не возвращались к увеличению количества методов и прочей математической составляющей модели, и сейчас это единственный представленный метод. На большинстве найденных систем он дает достаточную точность, чтобы получить картинки, похожие на изображения из других источников.
Модель принимает на вход:
В будущем можно добавить проверку, насколько представленная картинка совпадает с реальной, некоторые более сильные методы для моделирования (например, подключив библиотеку Boost.Numeric.Odeint) и еще какие-нибудь способы анализа, для которых наших знаний математики пока что не хватает.
Мы нашли наиболее популярные системы, описывающие странные аттракторы, чтобы получить на них максимальную производительность. Здесь хотим сказать спасибо сайту chaoticatmospheres.com, который очень сильно облегчил для нас этот поиск.
Все системы нужно было обернуть, чтобы, не смотря на то что они все «нашаблонены», их можно было класть в контейнер и нормально работать с ними в контроллере. Мы пришли к такому решению:
Мы начали работу по добавлению DynamicSystemWrapper, который бы владел DynamicSystem и мог проводить предобработку, нужную для визуализации (подбор константы для нормализации, допустимой погрешности для методов с контролем длины шага...), но закончить не успели.
В качестве библиотеки для визуализации мы выбрали OpenGL из-за производительности и ее возможностей, а также Qt5, где есть удобная обертка над OpenGL.
Для начала мы хотели научиться рисовать хоть что-то, и через некоторое время смогли сделать наш первый куб. Вскоре после этого появилась простая версия математической модели, и вот первая визуализация аттрактора:
С первой версией визуализации была готова и очень простая версия камеры. Она умела вращаться вокруг одной точки и приближаться/отдаляться. Нам хотелось большей свободы в пространстве: аттракторы разные, и их нужно по-разному исследовать. Тогда появилась вторая версия камеры, которая могла свободно вращаться и перемещаться во всех направлениях (мы ориентировались на камеру в Minecraft). В то время у нас только начиналась линейная алгебра, и поэтому знаний не хватало: много информации пришлось искать на просторах интернета.
Все это время картинки были белыми, статическими и неинтересными. Захотелось добавить цвета и динамики. Для начала мы научились раскрашивать всю картинку в один цвет, но это тоже оказалось неинтересно. Тогда нам пришло в голову следующее решение:
Получилось следующее:

Примерно такой схема осталась до конца.
Нам бросилось в глаза, что линии слишком «угловатые», и мы решили научиться их сглаживать. Конечно, мы попробовали уменьшить шаг моделирования, но, к сожалению, даже современные процессоры не в состоянии посчитать такое количество точек. Нужно было искать другой вариант.
Сначала мы подумали, что в OpenGL должно быть средство для сглаживания линий, но после долгих поисков обнаружили, что это не так. Тогда появилась идея интерполировать кривые и между каждой парой соседних точек, которые находятся достаточно далеко, добавить еще несколько. Для этого нужно было выбрать метод интерполяции кривых, а таких методов существует немало. Увы, большинство из них (например, кривая Безье) требовали указать еще несколько точек, что явно не подходило для нашей задачи: мы хотели, чтобы результат зависел только от того, что дала нам математическая модель. Через некоторое время мы нашли подходящую интерполяцию: кривую Катмулла — Рома. Получилось так:

После этого мы решили, что было бы неплохо записывать видео внутри приложения. Нам хотелось сохранить кроссплатформенность, поэтому мы остановились на библиотеке libav (выбора среди библиотек почти не было). К сожалению, вся библиотека написана на C и имеет очень неудобный интерфейс, поэтому нам понадобилось много времени, чтобы научиться записывать хоть что-то. Все последующие гифки сделаны с помощью встроенной записи.

До этого момента все цвета кривых явно указывались при создании. Мы решили, что для красивой картинки нужно задавать цвета по-другому. Для этого стали указывать только контрольные цвета, а остальные высчитывать по линейному градиенту. Эта часть была перенесена на шейдеры (до этого они были стандартными).
Нам показалось интересным раскрашивать траектории таким образом, чтобы у каждой из них цвет менялся от головы до хвоста. Это позволяет наблюдать эффект скорости:
Потом подумали, что стоит попытаться уменьшить время предобработки траектории: интерполировать кривую — это «дорогая» операция. Было принято решение перенести эту часть на шейдеры, чтобы GPU высчитывал интерполяцию каждый раз, когда его просят нарисовать часть траектории. Для этого мы использовали Geometry Shader. Такое решение дало много преимуществ: никакой задержки со стороны визуализации перед отрисовкой, возможность сглаживать кривые еще больше (подобные вычисления на GPU производятся быстрее, чем на CPU), использование меньшего количества оперативной памяти (до этого все интерполированные точки нужно было хранить, теперь — нет).
После выбора Qt5 как базового фреймворка вопрос выбора технологий для интерфейса отпал сразу. Встроенный Qt Creator в достаточной мере удовлетворяет все запросы маленького приложения.
Чтобы реагировать на пользовательские запросы, нужно было написать контроллер. Благо в Qt есть удобные способы обработки нажатия клавиш и ввода значений в поля. При этом используется главная идея Qt — механизм сигналов и слотов. Например, если в нашем приложении нажать кнопку, отвечающую за перестроение модели, будет выработан сигнал, который примет слот-обработчик. Он запустит само перестроение.
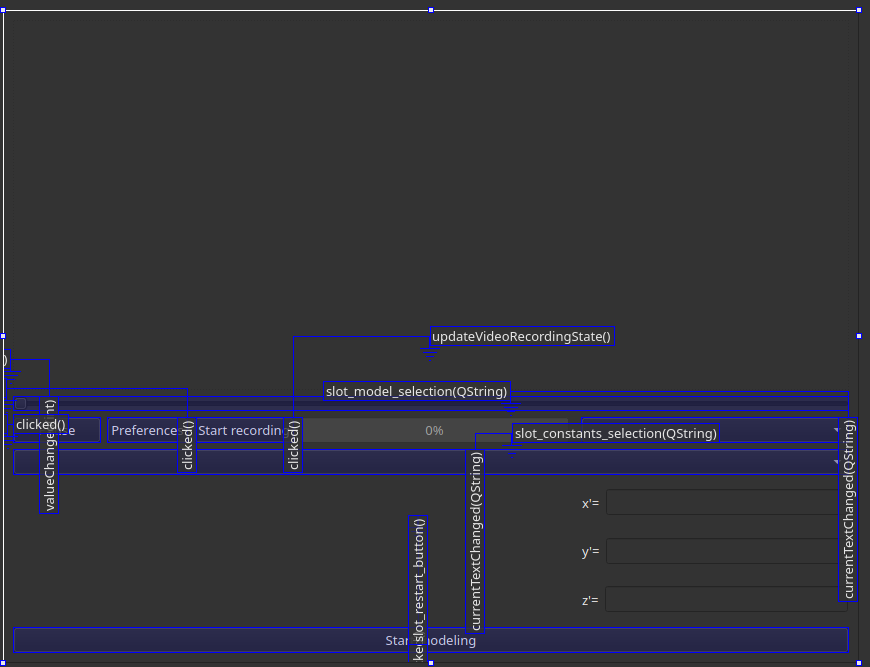
При разработке практически любого приложения с интерфейсом рано или поздно возникает идея сделать приложение многопоточным. Нам это показалось необходимым: построение встроенных моделей занимало несколько секунд, а построение пользовательской достигало 10 с. При этом, конечно, интерфейс зависал, ведь все вычисления велись в одном потоке. Довольно долго мы обсуждали разные варианты и думали про асинхронность с помощью std::async, но в итоге поняли, что хотим иметь возможность прерывать вычисления в другом потоке. Для этого пришлось написать обертку над std::thread. Все максимально просто: атомарный флаг для проверки и аккуратное прерывание, если проверка не прошла.
Это дало не только нужный результат — интерфейс перестал висеть — но еще добавило некоторую фичу: из-за особенностей архитектуры и взаимодействия между данными модели и визуализацией появилась возможность отрисовывать все онлайн, прямо по ходу подсчета. Раньше приходилось ждать все данные.
В приложении уже представлено много аттракторов, но мы также хотели дать возможность пользователю вводить уравнения самостоятельно. Для этого написали парсер, который поддерживает переменные (x, y, z), стандартные математические операции (+ — * / ^), константы, много математических функций (sin, cos, log, atan, sinh, exp и т.д.) и скобки. Вот как он работает:
Больше подробностей ищите в исходном коде парсера.
Каждый уровень возвращает какого-то наследника структуры Node. Всего их четыре:
У структуры Node есть только виртуальная функция calc, которая возвращает значение ее поддерева.
Полученные выходные данные очень удобно подстраиваются под ранее описанную архитектуру систем. В DynamicSystemInternal просто передается лямбда, хранящая указатели на корневые узлы трех полученных деревьев и позиции в памяти xyz значений. При вызове она меняет значения там на переданные и вызывает calc от корневых вершин.
В итоге мы получили программу, которая может визуализировать системы, заданные пользователем, и имеет базу из большого количества аттракторов. Делает она это достаточно красиво и оптимизировано, что не может не радовать.
Но работы еще много:
Наш репозиторий.
И еще несколько видео с аттракторами:
Некоторые аттракторы завораживают своей красотой даже на статических картинках. Мы захотели сделать приложение, которое сможет визуализировать большинство аттракторов в динамике, в 3D и без лагов.
О нас
Мы — Венедиктов Роман, Носивской Владислав и Карнаухов Кирилл — студенты второго курса бакалаврской программы «Прикладная математика и информатика» в НИУ ВШЭ — Санкт-Петербург. Программированием увлекаемся со школьных времен. Все трое занимались олимпиадным программированием и проходили в разные годы на заключительный этап Всероссийской олимпиады школьников по информатике, но опыта промышленного программирования раньше не имели, и для нас это первый большой командный проект. Мы защищали его в качестве курсовой работы по С++.
Моделирование
Есть много способов задать динамическую систему со странным аттрактором, но чаще всего встречается система из трех дифференциальных уравнений первого порядка. Мы начали с нее.
Перед тем, как что-то визуализировать, нужно промоделировать сам процесс и найти траектории точек. Точные методы моделирования достаточно трудоемкие, а нам хотелось бы делать это максимально быстро.
При реализации моделирования мы решили использовать метапрограммирование, отказавшись от std::function и других подобных механик. Они могли дать упрощение в архитектуре и написании кода, но сильно уменьшили бы производительность, а этого нам не хотелось.
Для моделирования исходно был использован простейший метод Рунге — Кутты 4-го порядка точности с постоянным шагом. Пока мы не возвращались к увеличению количества методов и прочей математической составляющей модели, и сейчас это единственный представленный метод. На большинстве найденных систем он дает достаточную точность, чтобы получить картинки, похожие на изображения из других источников.
Модель принимает на вход:
- функтор ‘derivatives’ для получения производных по координатам точки;
- функтор ‘observer’, который вызывается от точки, как только она получена;
- параметры моделирования (начальная точка, размер шага, количество точек).
В будущем можно добавить проверку, насколько представленная картинка совпадает с реальной, некоторые более сильные методы для моделирования (например, подключив библиотеку Boost.Numeric.Odeint) и еще какие-нибудь способы анализа, для которых наших знаний математики пока что не хватает.
Системы
Мы нашли наиболее популярные системы, описывающие странные аттракторы, чтобы получить на них максимальную производительность. Здесь хотим сказать спасибо сайту chaoticatmospheres.com, который очень сильно облегчил для нас этот поиск.
Все системы нужно было обернуть, чтобы, не смотря на то что они все «нашаблонены», их можно было класть в контейнер и нормально работать с ними в контроллере. Мы пришли к такому решению:
- класс DynamicSystem инстанцируется от типа функтора ‘observer’, хранит все параметры системы (название, уравнения...) и std::function ‘compute’. ‘Compute’ принимает почти то же, что и модель, но вместо функтора ‘derivatives’ ей подается на вход вектор значений констант системы.
- Эта std::function содержит в себе лямбду, которая хранит элемент класса DynamicSystemInternal и вызывает у него метод compute с такими же параметрами.
- DynamicSystemInternal инстанцируется уже и от типа ‘observer’, и от типа ‘derivatives’. Он получает по вектору констант системы сам функтор ‘derivatives’, который уже и передает модели вместе со всеми данными.
Мы начали работу по добавлению DynamicSystemWrapper, который бы владел DynamicSystem и мог проводить предобработку, нужную для визуализации (подбор константы для нормализации, допустимой погрешности для методов с контролем длины шага...), но закончить не успели.
Визуализация
В качестве библиотеки для визуализации мы выбрали OpenGL из-за производительности и ее возможностей, а также Qt5, где есть удобная обертка над OpenGL.
Для начала мы хотели научиться рисовать хоть что-то, и через некоторое время смогли сделать наш первый куб. Вскоре после этого появилась простая версия математической модели, и вот первая визуализация аттрактора:

С первой версией визуализации была готова и очень простая версия камеры. Она умела вращаться вокруг одной точки и приближаться/отдаляться. Нам хотелось большей свободы в пространстве: аттракторы разные, и их нужно по-разному исследовать. Тогда появилась вторая версия камеры, которая могла свободно вращаться и перемещаться во всех направлениях (мы ориентировались на камеру в Minecraft). В то время у нас только начиналась линейная алгебра, и поэтому знаний не хватало: много информации пришлось искать на просторах интернета.

Все это время картинки были белыми, статическими и неинтересными. Захотелось добавить цвета и динамики. Для начала мы научились раскрашивать всю картинку в один цвет, но это тоже оказалось неинтересно. Тогда нам пришло в голову следующее решение:
- Взять много (100–500, в настройках можно выбрать и больше, главное чтобы производительности хватало) близких друг к другу начальных точек.
- Смоделировать траекторию от каждой из них.
- Визуализировать траектории одновременно, при этом раскрасив их в разные цвета, и показывать только отрезок траектории.
Получилось следующее:

Примерно такой схема осталась до конца.
Нам бросилось в глаза, что линии слишком «угловатые», и мы решили научиться их сглаживать. Конечно, мы попробовали уменьшить шаг моделирования, но, к сожалению, даже современные процессоры не в состоянии посчитать такое количество точек. Нужно было искать другой вариант.
Сначала мы подумали, что в OpenGL должно быть средство для сглаживания линий, но после долгих поисков обнаружили, что это не так. Тогда появилась идея интерполировать кривые и между каждой парой соседних точек, которые находятся достаточно далеко, добавить еще несколько. Для этого нужно было выбрать метод интерполяции кривых, а таких методов существует немало. Увы, большинство из них (например, кривая Безье) требовали указать еще несколько точек, что явно не подходило для нашей задачи: мы хотели, чтобы результат зависел только от того, что дала нам математическая модель. Через некоторое время мы нашли подходящую интерполяцию: кривую Катмулла — Рома. Получилось так:

После этого мы решили, что было бы неплохо записывать видео внутри приложения. Нам хотелось сохранить кроссплатформенность, поэтому мы остановились на библиотеке libav (выбора среди библиотек почти не было). К сожалению, вся библиотека написана на C и имеет очень неудобный интерфейс, поэтому нам понадобилось много времени, чтобы научиться записывать хоть что-то. Все последующие гифки сделаны с помощью встроенной записи.

До этого момента все цвета кривых явно указывались при создании. Мы решили, что для красивой картинки нужно задавать цвета по-другому. Для этого стали указывать только контрольные цвета, а остальные высчитывать по линейному градиенту. Эта часть была перенесена на шейдеры (до этого они были стандартными).
Нам показалось интересным раскрашивать траектории таким образом, чтобы у каждой из них цвет менялся от головы до хвоста. Это позволяет наблюдать эффект скорости:

Потом подумали, что стоит попытаться уменьшить время предобработки траектории: интерполировать кривую — это «дорогая» операция. Было принято решение перенести эту часть на шейдеры, чтобы GPU высчитывал интерполяцию каждый раз, когда его просят нарисовать часть траектории. Для этого мы использовали Geometry Shader. Такое решение дало много преимуществ: никакой задержки со стороны визуализации перед отрисовкой, возможность сглаживать кривые еще больше (подобные вычисления на GPU производятся быстрее, чем на CPU), использование меньшего количества оперативной памяти (до этого все интерполированные точки нужно было хранить, теперь — нет).
Контроллер и пользовательский интерфейс
После выбора Qt5 как базового фреймворка вопрос выбора технологий для интерфейса отпал сразу. Встроенный Qt Creator в достаточной мере удовлетворяет все запросы маленького приложения.
Чтобы реагировать на пользовательские запросы, нужно было написать контроллер. Благо в Qt есть удобные способы обработки нажатия клавиш и ввода значений в поля. При этом используется главная идея Qt — механизм сигналов и слотов. Например, если в нашем приложении нажать кнопку, отвечающую за перестроение модели, будет выработан сигнал, который примет слот-обработчик. Он запустит само перестроение.

При разработке практически любого приложения с интерфейсом рано или поздно возникает идея сделать приложение многопоточным. Нам это показалось необходимым: построение встроенных моделей занимало несколько секунд, а построение пользовательской достигало 10 с. При этом, конечно, интерфейс зависал, ведь все вычисления велись в одном потоке. Довольно долго мы обсуждали разные варианты и думали про асинхронность с помощью std::async, но в итоге поняли, что хотим иметь возможность прерывать вычисления в другом потоке. Для этого пришлось написать обертку над std::thread. Все максимально просто: атомарный флаг для проверки и аккуратное прерывание, если проверка не прошла.
Это дало не только нужный результат — интерфейс перестал висеть — но еще добавило некоторую фичу: из-за особенностей архитектуры и взаимодействия между данными модели и визуализацией появилась возможность отрисовывать все онлайн, прямо по ходу подсчета. Раньше приходилось ждать все данные.
Пользовательские системы
В приложении уже представлено много аттракторов, но мы также хотели дать возможность пользователю вводить уравнения самостоятельно. Для этого написали парсер, который поддерживает переменные (x, y, z), стандартные математические операции (+ — * / ^), константы, много математических функций (sin, cos, log, atan, sinh, exp и т.д.) и скобки. Вот как он работает:
- Исходная строка запроса разбивается на лексемы. Далее лексемы разбираются слева направо и строится дерево выражения.
- Возможные операции разбиваются на группы. Для каждой группы — свой наследник Node. Группы: плюс-минус, умножение-деление, возведение в степень, унарный минус, так называемые листы (сюда входят константы, переменные, вызовы функций).
- Для каждой группы есть свой уровень вычислений. Каждый уровень вызывает рекурсивно вычисления на следующих уровнях. Можно заметить, что от порядка вызовов зависит распределение приоритетов операций. У нас они расположены в том порядке, в котором описаны выше.
Больше подробностей ищите в исходном коде парсера.
Каждый уровень возвращает какого-то наследника структуры Node. Всего их четыре:
- бинарный оператор — хранит указатели на двух детей и свой тип операции;
- унарный оператор — хранит указатель на ребенка и свой тип операции. Сюда входят и функции, так как это частный случай унарной операции;
- константа — хранит свое значение;
- переменная — хранит указатель на место в памяти, где лежит ее значение.
У структуры Node есть только виртуальная функция calc, которая возвращает значение ее поддерева.
Полученные выходные данные очень удобно подстраиваются под ранее описанную архитектуру систем. В DynamicSystemInternal просто передается лямбда, хранящая указатели на корневые узлы трех полученных деревьев и позиции в памяти xyz значений. При вызове она меняет значения там на переданные и вызывает calc от корневых вершин.
Итог
В итоге мы получили программу, которая может визуализировать системы, заданные пользователем, и имеет базу из большого количества аттракторов. Делает она это достаточно красиво и оптимизировано, что не может не радовать.
Но работы еще много:
- добавить более точные методы;
- добавить еще один слой обработки систем (нормализация и автоматический подбор ошибки в более сложных методах);
- улучшить работу с пользовательскими системами (поддержка переменных, сохранение);
- оптимизировать их работу (JIT компиляция или утилита, которая переводит сохраненные системы в c++ код и просто запускает перекомпиляцию, чтобы они достигли производительности встроенных систем);
- добавить возможности для анализа результатов или визуализации, которые реально нужны людям, которые работают с такими системами;
- …
Наш репозиторий.
И еще несколько видео с аттракторами: