Часть №1. Введение в биовычисления по сворачиванию. От белков к РНК
4 мин
Сразу надо сказать, что буду излагать вопрос о биовычислениях с определенной кибернетико-геометрической точки зрения. Это мое название и это направление не распространено. Уверен, что так будет легче понять тем кто не в теме этой биологической проблематики. Те кто уже в теме — готов и с вами подискутировать и показать почему традиционные методы не пригодны с точки зрения кибернетического подхода (но в этой статье не вы моя аудитория — уж извините, но уверен и вам она будет полезна как расширение мировоззрения на проблематику).
Практическое применение для биологов имеет больше вопрос сворачивания белков. В определенной степени очень много практических задач можно свести к этой задаче (знанию того как сворачивается белок), основная из которых — разработка лекарств по борьбе с вирусами и болезнями.
Но эта задача в общем виде не решена. Это как нерешенные задачи в математике, только с биологическим контекстом (см. парадокс Левинталя). Биологи могут лишь с определенной погрешностью увидеть путем биоэкспериментов состояние в уже свернутом состоянии, но проследить как это происходит пока не возможно. Но все это кроме того очень дорого. Почему и занимаются компьютерными вычислениями — это дешево, даже не смотря на то, что используется тысячи компьютеров в распределенных проектах.
Но введения хватит, далее с корабля на бал…
Практическое применение для биологов имеет больше вопрос сворачивания белков. В определенной степени очень много практических задач можно свести к этой задаче (знанию того как сворачивается белок), основная из которых — разработка лекарств по борьбе с вирусами и болезнями.
Но эта задача в общем виде не решена. Это как нерешенные задачи в математике, только с биологическим контекстом (см. парадокс Левинталя). Биологи могут лишь с определенной погрешностью увидеть путем биоэкспериментов состояние в уже свернутом состоянии, но проследить как это происходит пока не возможно. Но все это кроме того очень дорого. Почему и занимаются компьютерными вычислениями — это дешево, даже не смотря на то, что используется тысячи компьютеров в распределенных проектах.
Но введения хватит, далее с корабля на бал…


 В предыдущих статьях (
В предыдущих статьях (


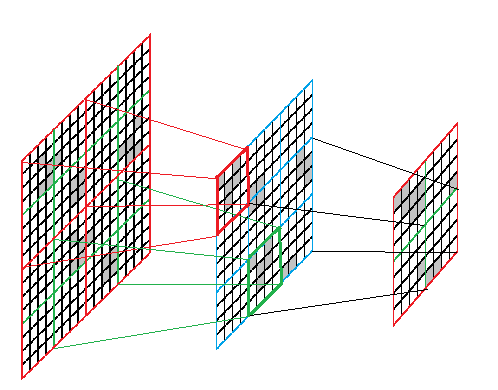
 Как видно по дискуссиям на хабре, несколько десятков хабровчан прослушали курс ml-class.org Стэнфордского университета, который провел обаятельнейший профессор Andrew Ng. Я тоже с удовольствием прослушал этот курс. К сожалению, из лекций выпала очень интересная тема, заявленная в плане: комбинирование обучения с учителем и обучения без учителя. Как оказалось, профессор Ng опубликовал отличный курс по этой теме — Unsupervised Feature Learning and Deep Learning (спонтанное выделение признаков и глубокое обучение). Предлагаю краткий конспект этого курса, без строгого изложения и обилия формул. В
Как видно по дискуссиям на хабре, несколько десятков хабровчан прослушали курс ml-class.org Стэнфордского университета, который провел обаятельнейший профессор Andrew Ng. Я тоже с удовольствием прослушал этот курс. К сожалению, из лекций выпала очень интересная тема, заявленная в плане: комбинирование обучения с учителем и обучения без учителя. Как оказалось, профессор Ng опубликовал отличный курс по этой теме — Unsupervised Feature Learning and Deep Learning (спонтанное выделение признаков и глубокое обучение). Предлагаю краткий конспект этого курса, без строгого изложения и обилия формул. В 
 теперь умеют умножать за
теперь умеют умножать за 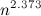 . Другими словами, доказано, что
. Другими словами, доказано, что 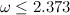 , где
, где 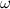 — экспонента умножения матриц. Доказала это совсем недавно
— экспонента умножения матриц. Доказала это совсем недавно 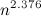 , полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты
, полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты 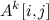 — количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время
— количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время 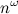 проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
 В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.
В заметке обсуждаются алгоритмы решета для поиска простых чисел. Мы подробно рассмотрим классическое решето Эратосфена, особенности его реализации на популярных языках программирования, параллелизацию и оптимизацию, а затем опишем более современное и быстрое решето Аткина. Если материал о решете Эратосфена предназначен в первую очередь уберечь новичков от регулярного хождения по граблям, то алгоритм решета Аткина ранее на Хабрахабре не описывался.