Comments 42
Стоит еще добавить тег «фракталы».
Спасибо Вам за эту красоту!
Спасибо Вам за эту красоту!
Как бы ненароком между вступлением к статье и тегами в конце читателю предоставляется возможность окунуться в красоту мира математики.
Спасибо, действительно интересно!
Спасибо, действительно интересно!
Не занудства ради, но всё же: не «корень из минус единицы равен i», а «квадрат i равен -1».
За статью, большое спасибо.
За статью, большое спасибо.
Меня всегда удивляли такие люди, в хорошем смысле. Теги ударные!
пост странное впечатление производит — как-будто хорошая книжка измазана говном
я не понимаю, почему у многих людей так тяжело укладывается в голове, что правила нужно соблюдать? к чему эта позиция мелкого пакостника?
я не понимаю, почему у многих людей так тяжело укладывается в голове, что правила нужно соблюдать? к чему эта позиция мелкого пакостника?
глубоко -)
так а какие правила?
так а какие правила?
habrahabr.ru/info/help/rules/
«Хабр — не для политики. На сайте крайне не приветствуются дискуссии на политические темы в любом их проявлении.»
«Хабр — не для политики. На сайте крайне не приветствуются дискуссии на политические темы в любом их проявлении.»
Хабр — не для правонарушителей… Говоря проще — запрещено обсуждать правила сайта...
habrahabr.ru/info/help/rules/
воу воу парень палехче, ты что правила сайта обсуждаешь? да ты анархист
Вы удивитесь, но политику много лет никто не трогал, пока политика не начала трогать нас.
по-моему, в интернетах достаточно профильных площадок, чтобы поделиться своими печалями
не туда, нада сюда было habrahabr.ru/post/206516/#comment_7114136
Можно просто траурную ленточку в углу всех картинок и разъяснение позиции про скорбь о свободе слова и информации в тегах.
Впечатление от поста испортил тег. Ну е-мое, ну как будто на заборе «ху*й» написали, как дети.
Это же «китайские мусульмане»!
Спасибо! Отличный пост.
Бассейном аттрактора к бесконечности A(∞) будем называть множество тех точек z, для которых траектории уходят в бесконечность, т.е. другими словами не сходятся к какой то неподвижной точке.
Эти понятия не эквивалентны. В общем случае бывает, что последовательность не стремится ни к бесконечности, ни к конкретной точке (а, например, осциллирует между двумя точками). Возможно, конкретно в данном случае траектория fn(z) всегда имеет предел (конечный или бесконечный), но это нужно отдельно доказывать.
То же самое касается выкладок в разделе «построение множества Жюлиа».
да точно, про осцилляторы совсем забыл упомянуть, спасибо за верное замечание, сейчас добавлю это уточнение в определение A(∞)
Так ведь случаи не исчерпываются тремя — «сходится к точке», «осциллирует между точками», «уходит в бесконечность».
Что, если последовательность осциллирует между неподвижной точкой и уходящей в бесконечность траекторией?
Что, если последовательность осциллирует между неподвижной точкой и уходящей в бесконечность траекторией?
т.е. дойдет до бесконечности и вернется обратно? -)
на самом деле суть одна, все это периодические точки, а в частном случае неподвижная точка — это периодическая с периодом равным единице
«сходится к точке», «осциллирует между точками»
на самом деле суть одна, все это периодические точки, а в частном случае неподвижная точка — это периодическая с периодом равным единице
Легко заметить,..
Как говорил мой научный руководитель, подобные обороты — явный признак того, что читатель «хрен повторит выводы автора». Но не в этом случае, т.к… и предыдущие выкладки я пониманию условно. С уважением отношусь к понимающим.
ну там где я это упомянул действительно легко заметить, что первые два члена это из общей квадратичной формы, а три слагаемых являются свободными
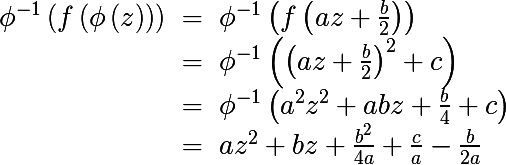
а вот тут я чот не рискнул писать, «легко заметить», что "Множество A(∞) (в вышеописанном контексте) является открытым, связным и неограниченным.".
я в последнем случае даже не пытался найти доказательство =)
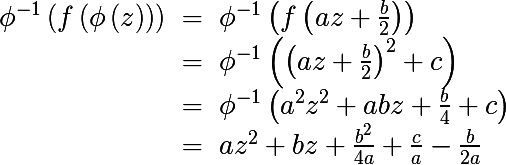
а вот тут я чот не рискнул писать, «легко заметить», что "Множество A(∞) (в вышеописанном контексте) является открытым, связным и неограниченным.".
я в последнем случае даже не пытался найти доказательство =)
Круто!
Кстати, меня всегда терзала мысль, что фракталы придумали производители обоев, а не Бенуа Мандельброт :)
Кстати, меня всегда терзала мысль, что фракталы придумали производители обоев, а не Бенуа Мандельброт :)
Мы в школе каждые полгода-год изучали новый язык. На каждом языке писали одни и те же программы. Программа для навигации по множеству Жюлиа или Мандельброта была одной из них.
Fractal Orgy — www.youtube.com/watch?v=zvHhnGjSmr8 и исходный код www.shadertoy.com/view/4dsGWB
Спасибо за статью.
Она мне очень кстати пришлась, поскольку «легла» на мои нынешние рассуждения над серьезными наборами экспериментальных данных.
Думаю, может в окрестностях этого поста я найду кого-нить, интересующегося изложенным выше с плавным переходом к «E.M.»-алгоритму и его применению к реально большим данным?..
А вдруг!
Она мне очень кстати пришлась, поскольку «легла» на мои нынешние рассуждения над серьезными наборами экспериментальных данных.
Думаю, может в окрестностях этого поста я найду кого-нить, интересующегося изложенным выше с плавным переходом к «E.M.»-алгоритму и его применению к реально большим данным?..
А вдруг!
ух ты, интересна связь этого поста и ем алгоритма =) мои контакты тут pavelnesterov.info/ пишите, пообщаемся
Связь, как я ее вижу:
f(z)=z^2+c,
А теперь представьте, что c=N(0,s^2) (хотя бы для примера, или что-нить случайное, но дискретное).
А вместо вашего «i» — давайте «по взрослому» не будем замыкаться в плоскости, а возьмем многомерное (бесконечномерное?...) пространство.
И скажите мне — не будет ли это все похоже на траекторию из оценок е.м.? Или траектория оценок е.м. похожа на «это»…
Я уже пол-года или больше «болею» этим вопросом.
Сам я его разрешить не в состоянии.
И при каких s они будут куда-нить плавненько сходиться?
А есть ли каки-нить хитрые условия, когда хоть парочка уровней фрактала" будет просматриваться невооруженным глазом.
Еще раз говорю — я могу заблуждаться.
Тогда просто считайте — это преддверие НГ.
А вообще у меня здесь лето и последний час последнего рабочего дня перед отпуском :)
Всех хабровчан с Новым Годом!
f(z)=z^2+c,
А теперь представьте, что c=N(0,s^2) (хотя бы для примера, или что-нить случайное, но дискретное).
А вместо вашего «i» — давайте «по взрослому» не будем замыкаться в плоскости, а возьмем многомерное (бесконечномерное?...) пространство.
И скажите мне — не будет ли это все похоже на траекторию из оценок е.м.? Или траектория оценок е.м. похожа на «это»…
Я уже пол-года или больше «болею» этим вопросом.
Сам я его разрешить не в состоянии.
И при каких s они будут куда-нить плавненько сходиться?
А есть ли каки-нить хитрые условия, когда хоть парочка уровней фрактала" будет просматриваться невооруженным глазом.
Еще раз говорю — я могу заблуждаться.
Тогда просто считайте — это преддверие НГ.
А вообще у меня здесь лето и последний час последнего рабочего дня перед отпуском :)
Всех хабровчан с Новым Годом!
Эх, на первых курсах универа писал программу, где строились разные варианты множеств Мандельброта, Жюлиа и Фату. С разными модификациями. И даже на университетской конференции про них рассказывал… В общем, спасибо за ностальгию! =)
Sign up to leave a comment.
Построение множества Жюлиа