В булевой алгебре, используемой для моделирования работы цифровых схем, не учитывается время перехода (или инертность) логических элементов (например, «И», «ИЛИ») из одного состояния в другое (например, из 0 в 1). В случаях, когда время распространения сигнала внутри элемента достаточно мало, задержку перехода можно не учитывать. Но с повышением частоты изменения входных сигналов в реальных схемах начинает сказываться влияние времени распространения сигнала внутри ее элементов. Такие задержки могут порождать неустойчивую работу устройств (т.е. в сигналах после последовательного прохождения через узлы схемы появляются не учитываемые моделью схемы переходы, называемые
сбоями). Многие производители современных процессоров держат в тайне, как они борются со сбоями, порождаемыми задержками, на частотах порядка ГГц. Ведь обычный проводник с множеством близких изгибов на плате в таком режиме работы уже превращается в индуктивность.
Чтобы проанализировать простейшие схемы на риски сбоя, обычно применяют метод временных диаграмм, ставший уже классическим. Сигналы в каждом узле прочерчиваются строго друг под другом; где нужно, производится искусственная задержка перехода из одного состояния в другое, а далее по булевому представлению строятся выходные сигналы. Данный метод не хорош тем, что требует работы с графиками, что может внести погрешность в получаемые сигналы. А нам нужно знать, возникнет ли сбой, и какой он будет иметь вид.
В 2005-м году я касался этой темы и изложил свои мысли в
данной заметке на английском языке. Однако мой хороший знакомый посоветовал написать в Хабрахабр для обсуждения с пользователями.
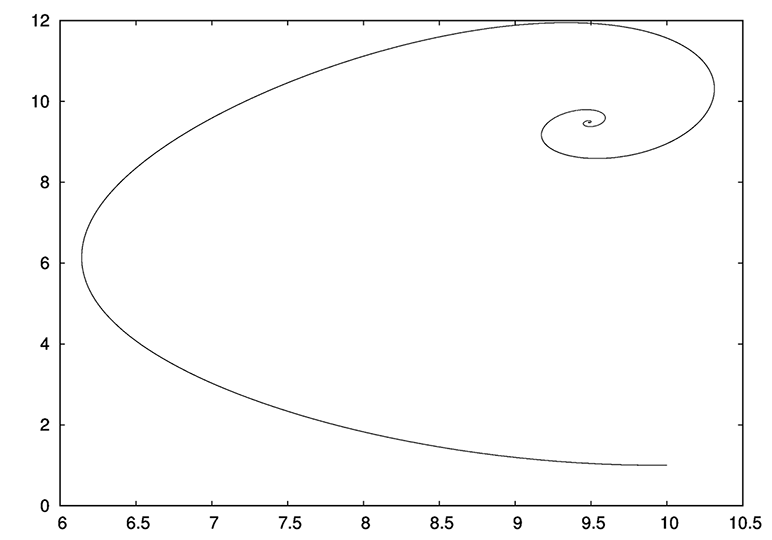
В данном топике процедура анализа схем переведена из графического представления в математическое представление. При этом вводится в булеву алгебру параметр «время» посредством замены логических операций арифметическими. Для простоты анализа рассматриваются асинхронные, т.е. неуправляемые внешним (синхронизирующим или тактирующим) сигналом, цифровые схемы.
Начнем…



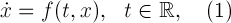
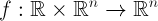 представляет собой сумму
представляет собой сумму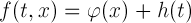
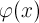 и тригонометрического полинома
и тригонометрического полинома 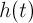 , являющегося
, являющегося 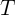 -периодической векторной функцией.
-периодической векторной функцией.