Добрый день, Хабрахабр. Это еще один пост в рамках моей программы по обогащению базы данных крупнейшего IT-ресурса информацией по алгоритмам и структурам данных. Как показывает практика, этой информации многим не хватает, а необходимость встречается в самых разнообразных сферах программистской жизни.
Я продолжаю преимущественно выбирать те алгоритмы/структуры, которые легко понимаются и для которых не требуется много кода — а вот практическое значение сложно недооценить. В прошлый раз это было
декартово дерево. В этот раз —
система непересекающихся множеств. Она же известна под названиями
disjoint set union (DSU) или
Union-Find.
Условие
Поставим перед собой следующую задачу. Пускай мы оперируем элементами
N видов (для простоты, здесь и далее — числами от 0 до N-1). Некоторые группы чисел объединены в множества. Также мы можем добавить в структуру новый элемент, он тем самым образует множество размера 1 из самого себя. И наконец, периодически некоторые два множества нам потребуется сливать в одно.
Формализируем задачу: создать
быструю структуру, которая поддерживает следующие операции:
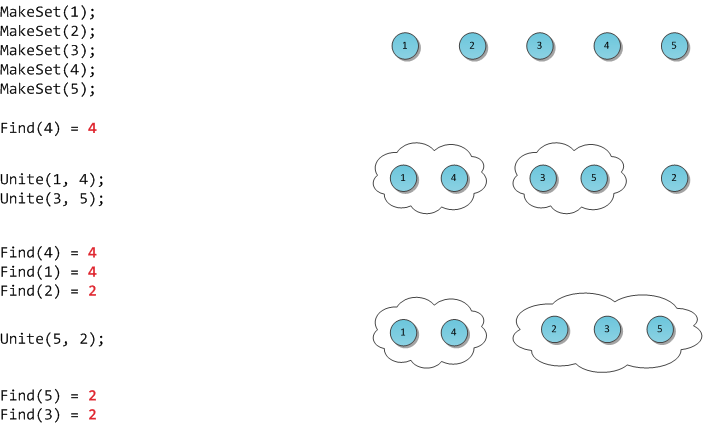
MakeSet(X) — внести в структуру новый элемент X, создать для него множество размера 1 из самого себя.
Find(X) — возвратить
идентификатор множества, которому принадлежит элемент X. В качестве идентификатора мы будем выбирать один элемент из этого множества —
представителя множества. Гарантируется, что для одного и того же множества представитель будет возвращаться один и тот же, иначе невозможно будет работать со структурой: не будет корректной даже проверка принадлежности двух элементов одному множеству
if (Find(X) == Find(Y)).
Unite(X, Y) — объединить два множества, в которых лежат элементы X и Y, в одно новое.
На рисунке я продемонстрирую работу такой гипотетической структуры.


 Не знаю как у вас, но у меня периодически возникает потребовать в онлайн-хранилище данных. Всегда есть файлы, которые могут потребоваться мне как на работе, так и дома – документация, фрагменты кода (snippets), наброски статей и т.д. Впрочем, иные документы, такие как карты, описания туристических маршрутов, материалы по истории городов и достопримечательностей могут понадобиться и вдалеке от родины. В первом случае можно обойтись синхронизацией данных домашнего и офисного компьютеров (что, кстати, не гарантирует вам отсутствие «головной боли»).
Не знаю как у вас, но у меня периодически возникает потребовать в онлайн-хранилище данных. Всегда есть файлы, которые могут потребоваться мне как на работе, так и дома – документация, фрагменты кода (snippets), наброски статей и т.д. Впрочем, иные документы, такие как карты, описания туристических маршрутов, материалы по истории городов и достопримечательностей могут понадобиться и вдалеке от родины. В первом случае можно обойтись синхронизацией данных домашнего и офисного компьютеров (что, кстати, не гарантирует вам отсутствие «головной боли»).