Оценка контента одна из главных составляющих формулы релевантности. Знание текстовых признаков и вклад каждого из них в оценку сайта позволит приблизиться к более профессиональной работе с ресурсом. В данной статье будет рассмотрена модель, позволяющая восстановить формулу ранжирования по каждому конкретному запросу, указана значимость определение тематики сайта при продвижении по определенному запросу, а также проработан вопрос, связанного с определением неестественного текста.
Восстановление формулы ранжирования
Если переводить данную задачу в область математики, то входные данные можно представить набором векторов, где каждый вектор – множество характеристик каждого сайта, а координаты в векторе – параметр, по которым оценивается сайт. В описанном векторном пространстве обязательно должна быть задана функция, определяющая отношение порядка двух объектов между собой. Эта функция позволяет ранжировать объекты между собой по принципу «больше — меньше», однако при этом сказать, насколько именно одно больше или меньше другого – нельзя. Такого вида задачи относятся к задачам оценки порядковой регрессии.
Наши сотрудники разработали алгоритм на основе модели линейной регрессии с регулируемой селективностью, который позволил с определенной долей погрешности восстановить ранги сайтов и спрогнозировать изменение выдачи при соответствующих корректировках параметров сайта. Первым шагом алгоритма является обучение модели. В данном случае обучающая выборка представляет собой результаты ранжирования сайтов в рамках одного поискового запроса. Упорядоченность сайтов в рамках поискового запроса фактически означает, что в признаковом пространстве существует некоторое направление, на которое объекты обучающей выборки должны проектироваться в нужном порядке. Это направление и является искомым в задаче восстановления формулы ранжирования. Однако судя по рис.1, таких направлений может быть много.
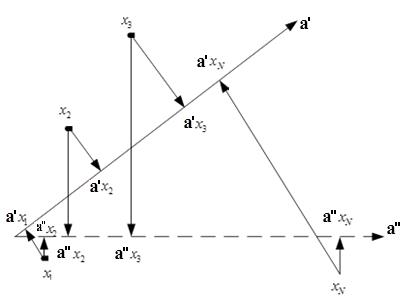
Рис. 1. Выбор направляющего вектора
Для решения данного вопроса был рассмотрен подход, лежащий в основе метода опорных точек, а именно – выбор такого направления, которое будет обеспечивать максимальное удаление объектов друг от друга.
Следующая задача, которая была решена — выбор стратегии обучения. Рассматривалось два варианта – сокращенная стратегия обучения, при которой учитывается порядок двух соответствующих элементов, и полная стратегия, которая учитывает весь порядок объектов. В результате экспериментов была выбрана сокращенная стратегия, которая заключается в решении следующего уравнения:(1)
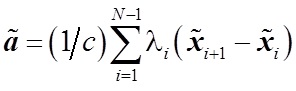
, где
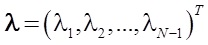
— решение стандартной задачи квадратичного программирования при линейных ограничениях:
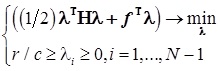
, где
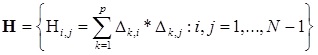
— симметричная матрица

— вектор коэффициента
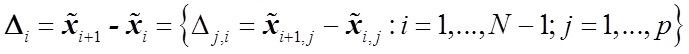
— разница векторов характеристик
Данный подход на различных выборках (100 признаков и 500 признаков на 20 различных множествах поисковых запросов) показал хорошие результаты (см. табл. 1).





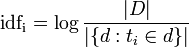

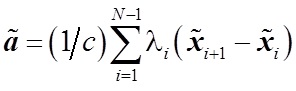 , где
, где 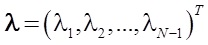 — решение стандартной задачи квадратичного программирования при линейных ограничениях:
— решение стандартной задачи квадратичного программирования при линейных ограничениях: 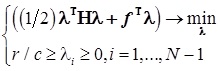 , где
, где 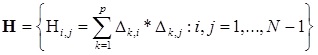 — симметричная матрица
— симметричная матрица  — вектор коэффициента
— вектор коэффициента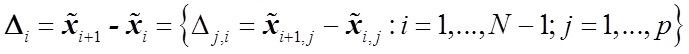 — разница векторов характеристик
— разница векторов характеристик

 Статья написана по материалам
Статья написана по материалам 