Алгоритмы *

Пример реализации метода быстрого марша(Fast Marching Method) для создания полей расстояний(Distance FIeld) и поиска кратчайшего пути.

Привет, Хабр!

Сейчас, когда вы слышите про ИИ в шахматах, наверняка первое, что приходит в голову – это AlphaZero, который "научился" играть в шахматы, превзойдя чемпионов мира, не имея никакого предварительного знания об игре. Но позвольте, это же только верхушка айсберга!

Не будем тратить время на объяснение того, как двигаются фигуры – это вы и так знаете. В сегодняшней статьи мы разберем алогоритм Minimax.

Не так давно прочитал статью "В поисках алгоритмического дзена", где автор обсуждает подходы к использованию алгоритмов в рабочих задачах. В статье подчеркивается, что даже наивная реализация конкретного алгоритма будет быстрее готовых средств/реализаций, существующих в платформе, и уж тем более будет быстрее специальный алгоритм для данного конкретного случая. Возникает ощущение, что использование самописных алгоритмов обладает абсолютным преимуществом над использованием готовых реализаций. С этой точкой зрения я не могу согласиться.

Стоит ли использовать специальные алгоритмы?

На этот вопрос нельзя дать однозначный ответ. Всё зависит от контекста, в котором будет работать алгоритм.

Если у нас хайлоад и метод находится в горячей секции, там самописные алгоритмы могут быть очень полезны, и использование более сложного в поддержке кода вполне оправдано.
В других случаях, я бы не стал торопиться добавлять алгоритмы, во всяком случае до проведения нагрузочных тестов, просмотра метрик системы и прочего.
В этой статье я постараюсь показать почему использование самописного алгоритма не всегда оправдано, даже если он работает значительно быстрее. А также предложу некоторый компромиссный вариант оптимизации.

Задание: необходимо создать кодовое слово (сокращенный вариант собственной фамилии и инициалов) по алгоритму А.С. Пушкина. Затем создать для полученного сокращения Micro QR Code вер. М2. Данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки просто страшно глючат, поэтому Ассоциация отказалась и от этого режима)

В настоящее время искусственный интеллект (ИИ) стремительно развивается. Мы являемся свидетелями интеллектуальной мощи таких нейросетей, как GPT-4 Turbo от OpenAI и Gemini Ultra от Google. В Интернете появляется огромное количество научных и популярных публикаций. Зачем же нужна еще одна статья про ИИ? Играя с ребенком в ChatGPT, я неожиданно осознал, что не понимаю значения аббревиатуры GPT. И, казалось бы, простая задача для айтишника, неожиданно превратилась в нетривиальное исследование архитектур современных нейросетей, которым я и хочу поделиться. Сгенерированная ИИ картинка, будет еще долго напоминать мою задумчивость при взгляде на многообразие и сложность современных нейросетей.

Задание: необходимо создать кодовое слово, состоящее из 8 цифр (на примере – 01234567) на основе алгоритма, частично приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.3, пример 2). Затем создать для полученного кода Micro QR Code вер. М2. Данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки просто страшно глючат, поэтому ассоциация отказалась от этого режима)

Задание: необходимо создать кодовое слово, состоящее из 8 цифр (на примере – 01234567) на основе алгоритма, приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.3, пример 2). Затем создать для полученного кода Micro QR Code вер. М2. Данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки просто страшно глючат, поэтому Ассоциация отказалась от этого режима)

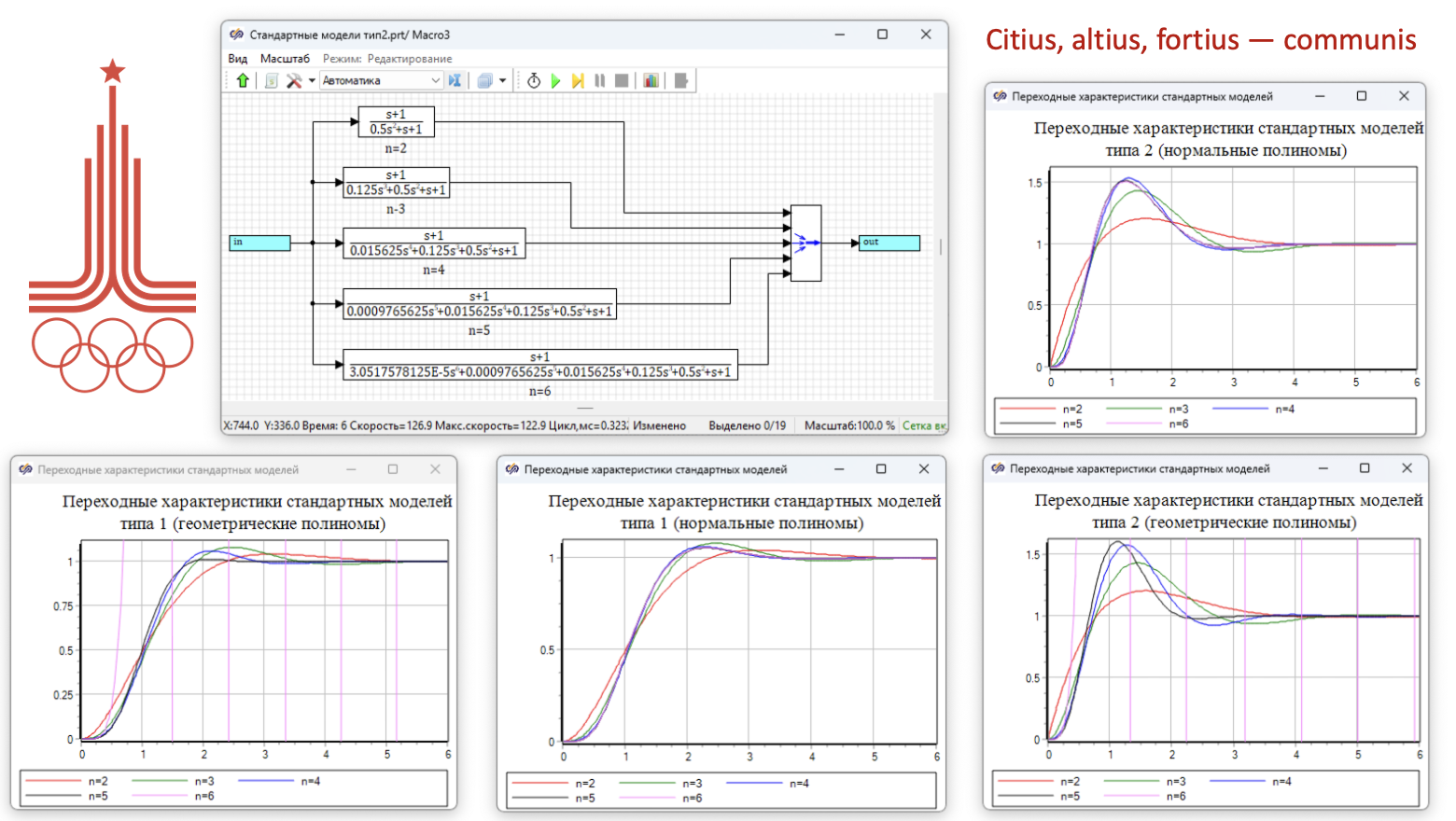
Ленонид Маркович Скворцов. Широко известный в узких кругах математик, профессионально занимающийся математическами проблемами автоматического управления. Например, его авторские методы использованы в SimInTech. Данный текст первая часть работы, которая еще готовится к публикации. Но с разрешения автора, читатели Хабр будут превыми кто сможет с ним ознакомится.

Все мы слышали, про преимущества советской математической школы над зарубежными математическими школами, но мало кто видел это приимущество в реальных задачах. В случае математических методов Леонида Марковича Скворцова, математика это не просто абстрактные формулы, а решение реальных прикладных задач, все можно увидеть пощупать и попробовать. В конце статьи видео-доказательство, практичесокй реализации преимуществ методов Леонида Марковича на практике.

Виртуальная трёхмерная среда максимальной приближенная к реальной физической на примере Выборгского залива с двумя робототехническими комплексами - БАС и БЭК

Задание: необходимо прочитать Micro QR Code версии М3, содержащий кодовое слово, на примере закодированных слов – Hello, Knowledge и KaDaBrAOK, на основе алгоритма, приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.5). Аналогично версии М2 данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки страшно глючат, поэтому Ассоциация отказалась и от этого режима)

Задание: необходимо прочитать Micro QR Code версии М3, содержащий кодовое слово, состоящее из символов верхнего регистра (на примере закодированных слов – SAFEBOX, Q1W2E3R4T5Y6U и EFB QWG WIFI 7; почему выбрано именно такое количество символов будет также расшифровано) на основе алгоритма, приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.4). Аналогично версии М2 данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки страшно глючат, поэтому Ассоциация отказалась и от этого режима).

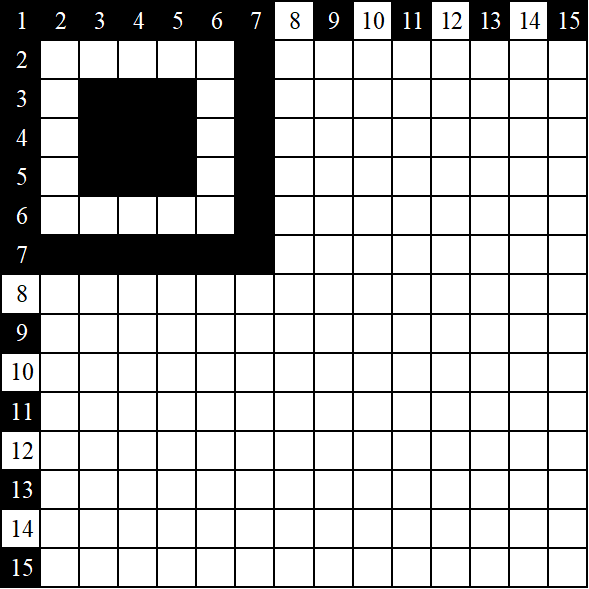
Задание: необходимо прочитать Micro QR Code версии М3, содержащий кодовое слово, состоящее из цифр (на примере – 777777777777777777 (18 цифр) и максимальном кодовом расстоянии (23 цифры) – 77777777777777777777777; почему выбрано именно такое количество цифр будет также расшифровано) на основе алгоритма, приведенного в ГОСТ Р ИСО/МЭК 18004-2015 (п. 7.4.3, пример 2). Аналогично версии М2 данный режим невозможно прочитать стандартными ресурсами мобильных устройств, производимых GAFAM (как оказалось, свободно распространяемые библиотеки страшно глючат, поэтому Ассоциация отказалась и от этого режима)

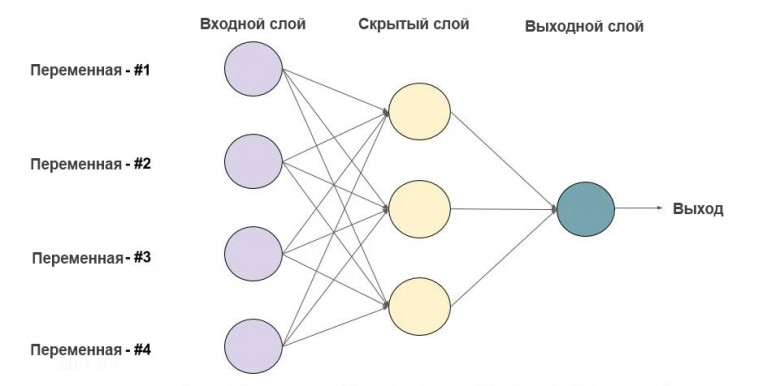
Генетический алгоритм нужен, когда ты знаешь параметры своей нейросети, но не знаешь, что должно получиться на выходе, например, этот алгоритм можно использовать для игры в Google динозаврика или Flappy Bird, потому что там ты не знаешь, что должно быть на выходе, но у тебя есть возможность сортировать наиболее жизнеспособные варианты, например по времени, это называется фитнес функций.

У меня никогда не получалось найти такой алгоритм и чтобы он работал, и был простым, и его можно было использовать, поэтому я приступил к созданию своего легкого, простого, прекрасно работающего Genetic Algorithm.

Моя цель не растянуть написания этой статьи, и замучить читателей её длиной, поэтому сразу приступим к коду. Как уже упоминалось, код простой, поэтому большую часть не нужно описывать целыми сочинениями.

Вначале нам потребуется импортировать модули:

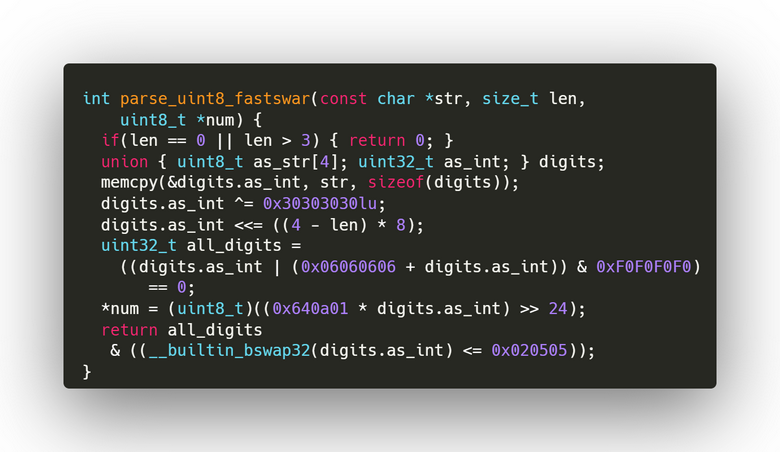
Допустим, вам нужно быстро распарсить 8-битные целые числа (0, 1, 2, …, 254, 255) из строки ASCII/UTF-8. Задача взята из проекта simdzone под руководством Йероена Коеккоека (NLnet Labs). Дана строка и её длина: например, ’22’ и длина 2. Наивное решение на C может выглядеть так:

$ echo "hector the frantic father on an anchor or a rare fat cat sat on the ranch" > test-huff.txt
$ xxd test-huff.txt
00000000: 6865 6374 6f72 2074 6865 2066 7261 6e74  hector the frant
00000010: 6963 2066 6174 6865 7220 6f6e 2061 6e20  ic father on an
00000020: 616e 6368 6f72 206f 7220 6120 7261 7265  anchor or a rare
00000030: 2066 6174 2063 6174 2073 6174 206f 6e20   fat cat sat on
00000040: 7468 6520 7261 6e63 680a                 the ranch.

a, c, e, f, h, i, n, o, r, s, t; пробел (0x20) и перевод каретки (0x0a).

$ 7z a -mx9 test-huff.txt.gz .\test-huff.txt
$ xxd test-huff.txt.gz
00000000: 1f8b 0808 d76f 6565 0200 7465 7374 2d68  .....oee..test-h
00000010: 7566 662e 7478 7400 158b 410a 0031 0c02  uff.txt...A..1..
00000020: effb 0abf 2621 257b 69c1 e6ff d480 1e64  ....&!%{i......d
00000030: c6ca e823 7425 96b8 fb0f 2c7a 0967 8393  ...#t%....,z.g..
00000040: 2873 8710 9543 11ee 75ad cc51 237d 0fc7  (s...C..u..Q#}..
00000050: 9797 d64a 0000 00                        ...J...

0101 1001 0001 1101 00111 010 000 1101 0101 1001 000
h    e    c    t    o     r   ' '   t    h  e    ' ' 

В этой статье мы познакомимся с бинарным поиском с примером на JavaScript, а так же сравним бинарный поиск и линейным.

Автоматизация процессов выглядит как задача без конца, не так ли?

Давайте подумаем, как можно упростить этот путь.

Существуют определенные стандарты программирования, которым нужно следовать разработчикам — зачем же они нужны?

Ответ лежит на поверхности: целью наших разработок, создаваемых совместно с вами, является облегчение ваших повседневных дел во внутренней энергетике бизнеса.

Когда программное решение превращается в препятствие, вместо того чтобы быть инструментом, возникает вопрос – зачем оно вообще нужно?

Привет! Меня зовут Илья Набатчиков, я MLE в компании Kamaz Digital. Также я являюсь учусь в онлайн магистратуре на базе университета ИТМО @ai-talent.

Сегодня я хочу рассказать о библиотеке ortools для решения проблемы маршрутизации транспортных средств с учетом ограничений по времени и грузоподъемности (CVRPTW).

И самое важно поделиться парой важных фичей, которых вы не найдете в документации.

В настоящее время набирают популярность модели Reinforcement Learning для решения прикладных задач бизнеса. В этой статье мы рассмотрим подмножество этих моделей, а именно многоруких бандитов (multi-armed bandits). Также мы:

- обсудим, какие задачи теоретически могут быть решены с помощью этих моделей;
- рассмотрим некоторые популярные реализации моделей многоруких бандитов;
- опишем симулятор ценообразования, применим эти алгоритмы в нём и сравним их эффективность.